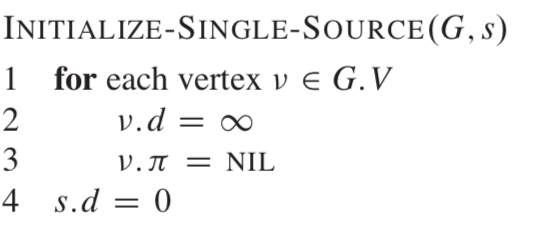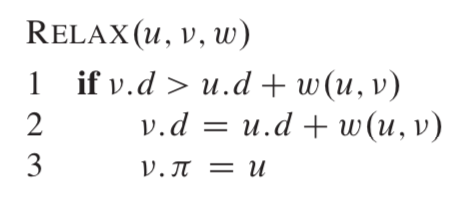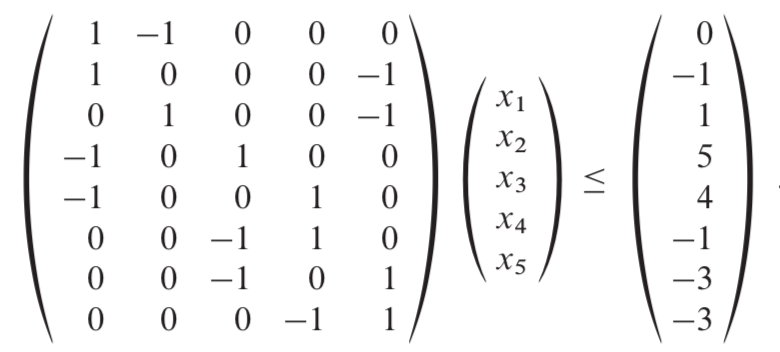《算法导论》单源最短路径笔记
问题描述:给定一个图G=(V,E),我们希望找到从给定源结点到每个结点v的最短路径
解决思路:两个结点之间的一条最短路径包含着其他的最短路径。
注:最短路径不能包含权重为负值的环路。当图中不含负权重边的时候我们可以使用Dijkstra算法来找到所有从源结点出发最短的路径。当图中含有负权重边的时候我们使用效率低一些的Bellman-Ford算法,在找寻最短路径的同时不断判断图中是否包含负权重环路。
1. 松弛操作(Relaxation)
我们将结点v的前驱记作v.pi,v到源点的最短距离为v.d。我们首先将d初始化为无穷大,pi初始化为NULL。
然后我们便可以使用任意一种寻找最短路径的算法来遍历图中的点并更新点到源点的最短路径了。
其中更新最短路径的操作也叫做放松(relax),伪代码如下:
2. Bellman-Ford
Bellman-Ford算法解决的是一般情况下的单源最短路径问题。通过对边进行松弛操作来渐进地降低从源结点s到每个结点v的最短路径,直到该估计值与实际的最短路径权重相同时为止。算法时间复杂度为O(VE)。
2. Dijkstra
Dijkstra算法利用了贪心策略
4. 差分约束和最短路径(Difference constraints and shortest paths)
线性规划中的一个特例可以被简化成单源最短路径问题。
常见线性规划问题的描述:
给定一个mXn的矩阵A、一个m维的向量b和一个n维的向量c。我们希望找到一个n维向量x,使得在由Ax<=b给定的m个约束条件下优化目标函数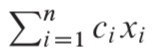
有时候,我们并不要求得到最优解,只需要找到一个可行解。
举个例子来说明:
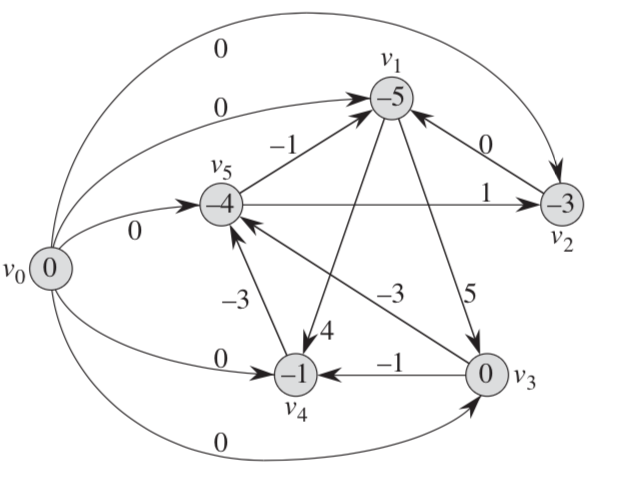
上面的不等式便是一个线性规划问题的约束条件,我们可以将其转换成一个约束图。我们将上面的mXn的矩阵A看作是一张由n个结点和m条边构成的图的领结矩阵的转置。对于i=1,2···,n,图中的每个结点vi对应n个未知变量xi中的一个。图中的每条有向边则对应m个不等式中的一个。
可以通过在对应的约束图中寻找最短路径来找到一个差分约束系统的解,证明见算法导论24章。
定理 给定差分约束系统Ax<=b,设G=(V,E)是该差分约束系统所对应的约束图。如果图G不包含权重为负值的环路,则
是系统的一个可行解。如果图G包含权重为负值的环路,则该系统没有可行解。