前向神经网络和 BP 算法详解 --- 之 DNN

前向神经网络和 BP 算法详解

一、神经网络的概念详解

1.1、人工神经网络的基础单元 — > 感知机

1.1.1、感知机模型讲解

• 首先我们需要明确一点就是，针对于拥有核函数的 SVM 或者多隐层 + 激活函数的多层神经网络，或者其他可以处理非线性可分的模型来说，感知机我们常称为神经元，但也可以看成是两层的神经网络( 即只有输入层和输出层，没有隐层 )，虽然它只能处理线性可分问题，但它依然是我们学习神经网络和深度学习的基石。
  
  
  
  
  
• 图中对应的符号含义如下：
  
  • 输入（x1 ，…，xn）
  • 偏移b 和 突触权重（w1 ，…，wn），注意，我们下面推到是使用 $\theta_i$ 代替 wi 进行公式推导。
  • 组合函数c（·）
  • 激活函数a（·）
  • 输出y
    
    
• 用数学的语言来说，如果我们有m个样本，每个样本对应于n维特征和一个二元类别输出，如下：
  $$(x_1^{(0)}, x_2^{(0)}, ...x_n^{(0)}, y_0), (x_1^{(1)}, x_2^{(1)}, ...x_n^{(1)},y_1), ... (x_1^{(m)}, x_2^{(m)}, ...x_n^{(m)}, y_m)$$
• 我们的目的便是找一个超平面，即： $\theta_0 + \theta_{1}x_1 + ... + \theta_{n}x_{n} = 0$ 让把每个类别的样本特征带入该方程时，要么大于 0 ，要么小于 0,从而使得样本分居在超平面两侧，从而到达线性可分。一般如果样本线性可分，则这样的超平面会有多个解，不唯一。
  
  
• 为了简化模型，我们增加一个 x0 = 1，使得超平面方程简写为 $\sum\limits_{i=0}^{n}\theta_{i}x_{i} = 0$ 进一步可写向量形式为 $\theta \bullet x = 0$ 其中 $\theta$ 和 X 均为 n * 1 的向量，$\bullet$为内积，下面我们都用它表示超平面。
• 故感知机的模型可以定义为 $y = sign(\theta \bullet x)$ ,其中sign 为激活函数，它是符号函数，也称为阶跃函数。
  $$sign(x)= \begin{cases} -1& {x<0}\\ 1& {x\geq 0} \end{cases}$$
  
  
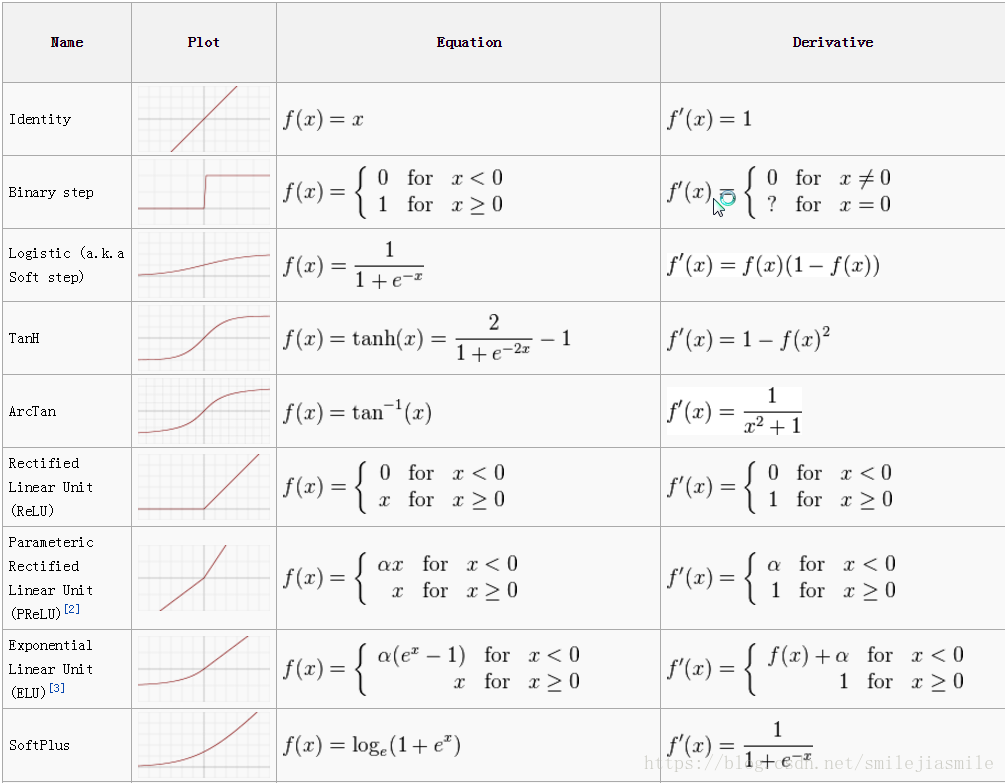
• 在多层神经网络中，我们可能用到其他的激活函数,如下：

1.1.2 感知机模型损失函数

• 根据上面的分析，我们将 $\theta \bullet x > 0$的样本类别输出值取为1 ，而小于 0 的样本类别取为 -1，这样定义它的好处便是方便我们定义损失函数。因为有了上面的约定，正确分类的样本满足： $y\theta \bullet x > 0$,而错误的分类样本满足 $y\theta \bullet x < 0$。于是损失函数的优化方法便是期望使误分类的所有样本，到超平面的距离之和最小(即想让误分类样本逐渐消失)。
  
  
• 由于$y\theta \bullet x < 0$，所以对于每一个误分类的样本 i，到超平面的距离为： $$- y^{(i)}\theta \bullet x^{(i)}\big / ||\theta||_2$$
• 其中，$||\theta||_2$ 为 L2范数。(若此处距离公式不理解，可自行查阅点到直线的距离，或者学习相关的机器学习相关章节)
• 接着，我们假设所有误分类的点的集合为M，则所有误分类的样本到超平面的距离之和为：
  $$- \sum\limits_{x_i \in M}y^{(i)}\theta \bullet x^{(i)}\big / ||\theta||_2$$
  这样，我们便得到了初步的感知机模型的损失函数。
• 之外，我们还需要对它进行简化，我们可以观察到，分子分母都有 $\theta$(即分子分母具有相同的扩大倍数)，当分子的 $\theta$ 扩大 N 倍时，其分母的 L2 范数也会扩大 N 倍。因为我们研究的是最值化问题，故我们可以固定分子或者分母为 1，然后求解剩下的另一个分子的最小化或者分母的倒数的最小化，然后将其作为损失函数。这样做可以简化我们的损失函数，便于后面问题的求解。 注意：在感知机模型中，我们采用的是保留分子，固定分母为 1，即最终感知机的损失函数为：
  $$J(\theta) = - \sum\limits_{x_i \in M}y^{(i)}\theta \bullet x^{(i)}$$
  之外，我们还需要注意的就是，针对 SVM 来说，它采用的就是固定分子为1，然后求解 $\frac{1}{||\theta||_2}$ 的最大化问题(为什么是最大化问题，而不是最小化问题，这和 SVM 的优化思想有关，这里不做额外介绍了。)

1.1.3 感知机的损失函数优化方法、与算法流程描述

1.1.3.1 优化方法

• 经过上面的推理，我们得到了感知机的损失函数，$J(\theta) = - \sum\limits_{x_i \in M}y^{(i)}\theta \bullet x^{(i)}$, 其中 M 是所有误分类的点的集合，并且它是一个凸函数，可用梯度下降或者拟牛顿法，常用 SGD(随机梯度下降)，这就意味着每次仅仅需要使用一个误分类的点来更新梯度。由于我们的损失函数里面有限定，只有误分类的 M 集合里面的样本才能参加损失函数的优化。故不能用 BGD(批量梯度下降)，只能用 SGD 或者 MSGD(小批量梯度下降)。
• 损失函数针对 $\theta$向量的偏导数为：
  $$\frac{\partial}{\partial \theta}J(\theta) = - \sum\limits_{x_i \in M}y^{(i)}x^{(i)}$$
• $\theta$ 的梯度下降公式为：
  $$\theta = \theta + \alpha\sum\limits_{x_i \in M}y^{(i)}x^{(i)}$$
• 由于我们采用随机梯度下降，每次仅采用一个误分类样本来计算梯度，假设采用第 i 个样本来更新梯度，则简化后的 $\theta$ 的梯度下降迭代公式为：
  $$\theta = \theta + \alpha y^{(i)}x^{(i)}$$
• 其中 α 为步长，$y^{(i)}$ 为样本输出1或者-1， x(i)为(n+1) x 1的向量。

1.1.3.2 算法描述

• 这里我们对上面的讨论做个总结，汇成算法流程。
  
  
• 算法输入
  
  • 算法的输入为m个样本，每个样本对应于n维特征和一个二元类别输出1或者-1，如下：
    $$(x_1^{(0)}, x_2^{(0)}, ...x_n^{(0)}, y_0), (x_1^{(1)}, x_2^{(1)}, ...x_n^{(1)},y_1), ... (x_1^{(m)}, x_2^{(m)}, ...x_n^{(m)}, y_m)$$
• 输出：
  
  • 分离超平面的模型系数θ向量
    
    
• 算法执行流程：
  
  • 定义所有x0为1。选择θ向量的初值和 步长α的初值。可以将θ向量置为0向量，步长设置为1。要注意的是，由于感知机的解不唯一，使用的这两个初值会影响θ向量的最终迭代结果。
  • 在训练集里面选择一个误分类的点 $(x_1^{(i)}, x_2^{(i)}, ...x_n^{(i)}, y_i)$, 用向量表示即$(x^{(i)}, y^{(i)})$，这个点应该满足：$y^{(i)}\theta \bullet x^{(i)} < 0$
  • 对 θ 向量进行一次随机梯度下降的迭代：$θ = θ+ αy^{(i)} x^{(i)}$
  • 检查训练集里是否还有误分类的点，如果没有，算法结束，此时的θ向量即为最终结果。如果有，继续第2步。
    
    
• 最后，还需要提及一点的就是，在以前实际实现算法的时候，我们都采用的是感知机算法的对偶形式去进行求解参数，优化模型，因为它可以优化算法的执行速度。读者可自行 Google 学习。我们还是把重点放到下面的神经网络相关知识的讲解。

1.2 深度神经网络(DNN) 与前向传播算法

1.2.1 深度神经网络简介

• 从感知机可知，它只能用于二元分类问题，不能解决非线性问题，神经网络在它之上做了很多扩展，主要体现在如下几个方面：
  
  • 加入了隐藏层，隐藏层可以有多层，增强模型的表达能力，故其复杂度也增加了很多。
  • 输入层神经元不止一个，有多个输出。此外，在上一层与下一层之间为全连接，同层神经元之间无连接，相互独立。这样模型可以灵活的应用于分类和回归(一般区别只在与结构最后一程的激活函数，如果要做回归，需要一个连续值，就不要用类似 Sigmoid 的标准化挤压函数)
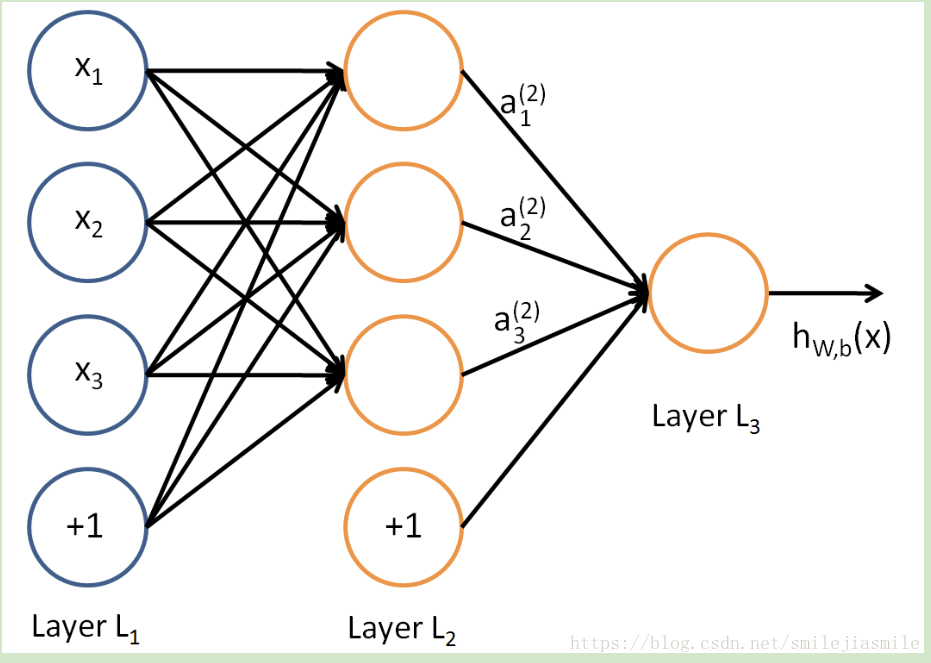
  • 对激活函数做了扩展，将 Sign(z) 替换成 Sigmod 函数，或者其他激活函数，tanx,softmax, ReLU等。于是就成了类似下图的样子：
    
    

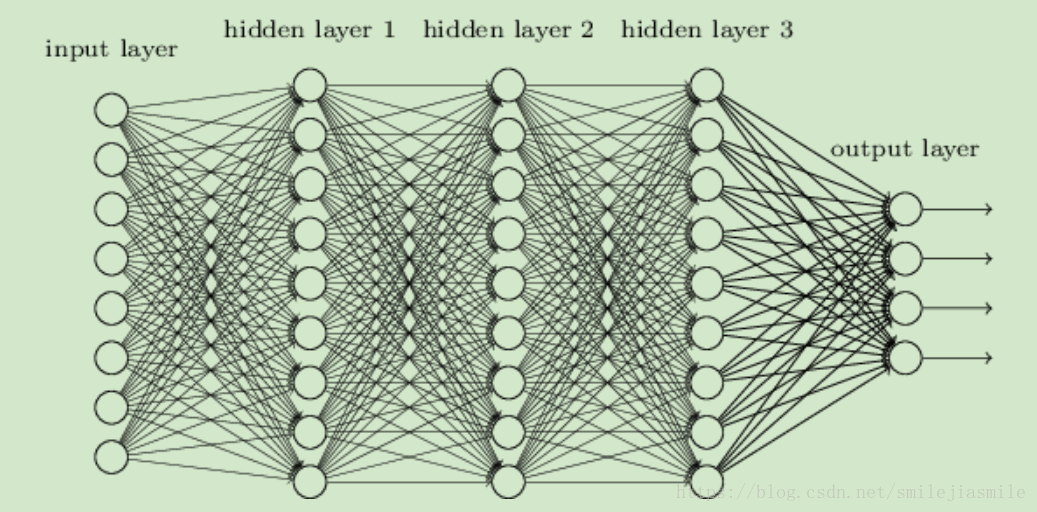
• DNN 我们可以理解为多隐层的神经网络，此外，它有时也叫多层感知机（Multi-Layer perceptron,MLP），它内部的神经网络层分为三类，输入层，隐藏层和输出层,如上图，一般来说第一层是输入层，最后一层是输出层，而中间的层数都是隐藏层。层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样，即一个线性关系$z=\sum\limits w_ix_i + b$ 加上一个激活函数σ(z) 。不过由于层数增多，线性关系 W 和偏置 b 的数量也增多了。具体如下定义：
  
  

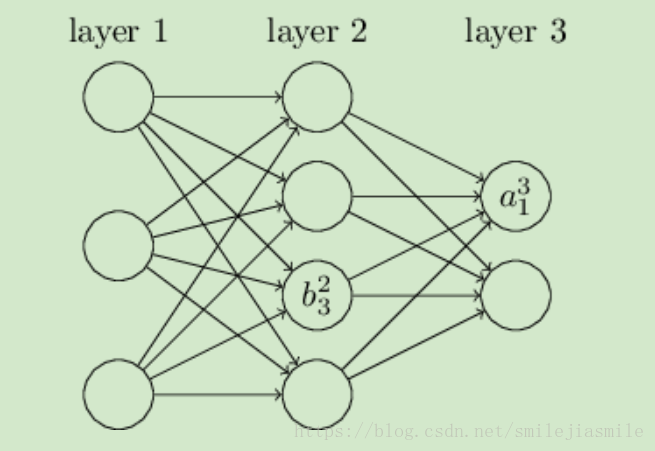
• 首先我们来看看线性关系系数w的定义。以下图一个三层的DNN为例，第二层的第4个神经元到第三层的第2个神经元的线性系数定义为 $w_{24}^3$ 上标3代表线性系数w所在的层数，而下标对应的是输出的第三层索引2和输入的第二层索引4。你也许会问，为什么不是 $w_{42}^3$,而是$w_{24}^3$呢 ？ 这主要是为了便于模型用于矩阵表示运算，如果是 $w_{42}^3$ 而每次进行矩阵运算是 $w^Tx+b$,需要进行转置。将输出的索引放在前面的话，则线性运算中对权重 W 不用转置。即，第 l−1 层的第 k 个神经元到第 l 层的第 j 个神经元的线性系数定义为 $w_{jk}^l$,其中输入层是没有 w 参数的。
  
  

  
  
  

• 再来看看偏倚b的定义。还是以这个三层的DNN为例，第二层的第三个神经元对应的偏倚定义为$b_3^{2}$ 其中，上标2代表所在的层数，下标3代表偏倚所在的神经元的索引。同样的道理，第三个的第一个神经元的偏倚应该表示为 $b_1^{3}$,同理输入层没有偏倚参数 b。

  

1.2.2 前向传播算法

• 上面，我们已经介绍了DNN各层线性关系系数w,偏倚b的定义。假设我们选择的激活函数是σ(z)，隐藏层和输出层的输出值为a，则对于下图的三层DNN,利用和感知机一样的思路，我们可以利用上一层的输出计算下一层的输出，也就是所谓的DNN前向传播算法。
  
  

  
  
  

• 对于第二层的的输出 $a_1^2,a_2^2,a_3^2$,我们有：
  
  • $a_1^2=\sigma(z_1^2) = \sigma(w_{11}^2x_1 + w_{12}^2x_2 + w_{13}^2x_3 + b_1^{2})$
  • $a_2^2=\sigma(z_2^2) = \sigma(w_{21}^2x_1 + w_{22}^2x_2 + w_{23}^2x_3 + b_2^{2})$
  • $a_3^2=\sigma(z_3^2) = \sigma(w_{31}^2x_1 + w_{32}^2x_2 + w_{33}^2x_3 + b_3^{2})$
• 对于第三层的的输出 $a_1^3$,我们有：
  
  • $a_1^3=\sigma(z_1^3) = \sigma(w_{11}^3a_1^2 + w_{12}^3a_2^2 + w_{13}^3a_3^2 + b_1^{3})$
• 将上面的例子一般化，假设第l−1层共有m个神经元，则对于第l层的第j个神经元的输出$a_j^l$，我们有：
  $$a_j^l = \sigma(z_j^l) = \sigma(\sum\limits_{k=1}^mw_{jk}^la_k^{l-1} + b_j^l)$$
• 其中，如果$l$=2,则对于的 a_k^1,即为输入层的$x_k$ 。
  
  
• 下面，重点来了，矩阵表示法，因为代数法表示输出复杂，而矩阵法表示输出简洁。假设第 $l$−1 层共有m个神经元，而第l层共有n个神经元，则第 $l$ 层的线性系数w组成了一个 n×m 的矩阵Wl, 第 $l$ 层的偏倚 b 组成了一个n×1的向量$b^l$ , 第 $l$−1 层的的输出a组成了一个m×1的向量 $a^{l-1}$，第 $l$ 层的的未激活前线性输出z组成了一个 n×1 的向量 $z^l$, 第 $l$ 层的的输出a组成了一个n×1的向量$a^l$。则用矩阵法表示，第 $l$ 层的输出为：
  $$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$$
• 它表示非常简洁，故后面的讨论会基于这个矩阵法表示来推导。
  
  
• 算法流程描述：
  
  • 输入: 总层数 L，所有隐藏层和输出层对应的矩阵 W,偏倚向量 b，输入值向量x
  • 输出：输出层的输出 $a^L$
  • 流程：
    
    • 初始化 $a^1$ =x
    • for $l$ =2 to $L$ 计算：
      $$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$$
    • 最后的结果即为输出 $a^L$
      
      
• DNN前向传播算法，这一大堆的矩阵W,偏倚向量b对应的参数怎么获得呢？怎么得到最优的矩阵W,偏倚向量b呢？这就得靠 DNN 的反向传播算法来解决了。而理解反向传播算法的前提就是理解DNN的模型与前向传播算法。接下来，便是传说中的 BP算法。

1.3 反向传播算法 BP (Back Propagation)

1.3.1 反向传播要解决的问题

• 在了解DNN的反向传播算法前，我们先要知道DNN反向传播算法要解决的问题，也就是说，什么时候我们需要这个反向传播算法 ？
  
  
• 回到我们监督学习的一般问题，假设我们有m个训练样本：$\{(x_1,y_1), (x_2,y_2), ..., (x_m,y_m)\}$ ,其中 x 为输入向量，特征维度为 n_in,而 y 为输出向量，特征维度为 n_out。我们需要利用这 m 个样本训练出一个模型，当有一个新的测试样本 ($x_{test}$, ? ) 来到时, 我们可以预测$y_{test}$向量的输出。
  
  
• 如果我们采用 DNN 的模型，即我们使输入层有 n_in 个神经元，而输出层有n_out 个神经元。再加上一些含有若干神经元的隐藏层。此时我们需要找到合适的所有隐藏层和输出层对应的线性系数矩阵 W,偏倚向量 b,让所有的训练样本输入计算出的输出尽可能的等于或很接近样本输出。怎么找到合适的参数呢 ？
  
  
• 大家可能会联想到可以用一个合适的损失函数来度量训练样本的输出损失，接着对这个损失函数进行优化求最小化的极值，对应的一系列线性系数矩阵 W,偏倚向量 b 即为我们的最终结果。在DNN中，损失函数优化极值求解的过程一般是通过梯度下降法来一步步迭代完成的，当然也可以是其他的迭代方法比如牛顿法与拟牛顿法。
  
  
• 对DNN的损失函数用梯度下降法进行迭代优化求极小值的过程即为我们的反向传播算法。

1.3.2 反向传播的算法的基本思想

• 在进行DNN反向传播算法前，我们需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。你也许会问：训练样本计算出的输出是怎么得来的？这个输出是随机选择一系列 W, b,用我们上一节的前向传播算法计算出来的。即通过一系列的计算： $a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$ 。计算到输出层第L层对应的 $a^L$ 即为前向传播算法计算出来的输出。 - 回到损失函数，DNN可选择的损失函数有不少，为了专注算法，这里我们使用最常见的均方差来度量损失。即对于每个样本，我们期望最小化下式 ：
  $$J(W,b,x,y) = \frac{1}{2}||a^L-y||_2^2$$
• 其中，$a^L$ 和 y 为特征维度为 n_out 的向量,而 $||S||_2$ 为S 的 L2 范数。
• 损失函数有了，现在我们开始用梯度下降法迭代求解每一层的 W, b。
• 首先是输出层第 L 层。注意到输出层的 W,b 满足下式：
  $$a^L = \sigma(z^L) = \sigma(W^La^{L-1} + b^L)$$
• 这样对于输出层的参数，我们的损失函数变为：
  $$J(W,b,x,y) = \frac{1}{2}||a^L-y||_2^2 = \frac{1}{2}|| \sigma(W^La^{L-1} + b^L)-y||_2^2$$
  
  
• 这样求解W,b的梯度就简单了：
  $$\frac{\partial J(W,b,x,y)}{\partial W^L} = \frac{\partial J(W,b,x,y)}{\partial z^L}\frac{\partial z^L}{\partial W^L} =(a^L-y) \odot \sigma^{'}(z^L)(a^{L-1})^T$$
  $$\frac{\partial J(W,b,x,y)}{\partial b^L} = \frac{\partial J(W,b,x,y)}{\partial z^L}\frac{\partial z^L}{\partial b^L} =(a^L-y)\odot \sigma^{'}(z^L)$$
  
  
• 注意上式中有一个符号 $\odot$, 它代表Hadamard积，对于两个维度相同的向量 $A（a_1,a_2,...a_n）^T$ 和 $B（b_1,b_2,...b_n）^T$ ,则 $A \odot B = (a_1b_1, a_2b_2,...a_nb_n)^T$
  
  
• 我们注意到在求解输出层的W,b的时候，有公共的部分 $\frac{\partial J(W,b,x,y)}{\partial z^L}$ 因此我们可以把公共的部分即对$z_L$先算出来，记为：
  $$\delta^L = \frac{\partial J(W,b,x,y)}{\partial z^L} = (a^L-y)\odot \sigma^{'}(z^L)$$
  
  
• 现在我们终于把输出层的梯度算出来了，那么如何计算上一层 L−1 层的梯度，上上层 L−2 层的梯度呢？这里我们需要一步步的递推，注意到对于第l层的未激活输出$z^l$，它的梯度可以表示为:
  $$\delta^l =\frac{\partial J(W,b,x,y)}{\partial z^l} = \frac{\partial J(W,b,x,y)}{\partial z^L}\frac{\partial z^L}{\partial z^{L-1}}\frac{\partial z^{L-1}}{\partial z^{L-2}}...\frac{\partial z^{l+1}}{\partial z^{l}}$$
  
  
• 如果我们可以依次计算出第$l$层的$δ^l$,则该层的$W^l$,$b^l$很容易计算？y因为根据前向传播算法，我们有： $z^l= W^la^{l-1} + b^l$
  
  
• 所以根据上式我们可以很方便的计算出第 $l$ 层的 $W^l$, $b^l$ 的梯度如下：
  $$\frac{\partial J(W,b,x,y)}{\partial W^l} = \frac{\partial J(W,b,x,y)}{\partial z^l} \frac{\partial z^l}{\partial W^l} = \delta^{l}(a^{l-1})^T$$
  $$\frac{\partial J(W,b,x,y)}{\partial b^l} = \frac{\partial J(W,b,x,y)}{\partial z^l} \frac{\partial z^l}{\partial b^l} = \delta^{l}$$
• 那么现在问题的关键就是要求出 $δ^l$ 了。这里我们用数学归纳法，第 L 层的$δ^L$上面我们已经求出，假设第 $l$+1 层的$δ^{l+1}已经求出来了，那么我们如何求出第$l$层的$δ^l$ 呢？我们注意到：(链式法则)

扫描二维码关注公众号，回复： 2001724 查看本文章

$$\delta^{l} = \frac{\partial J(W,b,x,y)}{\partial z^l} = \frac{\partial J(W,b,x,y)}{\partial z^{l+1}}\frac{\partial z^{l+1}}{\partial z^{l}} = \delta^{l+1}\frac{\partial z^{l+1}}{\partial z^{l}}$$

• 可见，用归纳法递推 $δ^{l+1}$ 和 $δ^l$ 的关键在于求解 $\frac{\partial z^{l+1}}{\partial z^{l}}$
  
  
• 而 $z^{l+1}$ 和 $z^l$ 的关系其实很容易找出：
  $$z^{l+1}= W^{l+1}a^{l} + b^{l+1} = W^{l+1}\sigma(z^l) + b^{l+1}$$
  
  
• 这样很容易求出：
  $$\frac{\partial z^{l+1}}{\partial z^{l}} = (W^{l+1})^T\odot \underbrace{(\sigma^{'}(z^l),..,\sigma^{'}(z^l))}_{n_{l+1}}$$
  
  
• 将上式带入上面 $δ^{l+1}$ 和 $δ^l$ 关系式我们得到：
  $$\delta^{l} = \delta^{l+1}\frac{\partial z^{l+1}}{\partial z^{l}} = (W^{l+1})^T\delta^{l+1}\odot \sigma^{'}(z^l)$$
  
  
• 现在我们得到了 $δ^l$ 的递推关系式，只要求出了某一层的 $δ^l$ ，求解$W^l$,$b^l$ 的对应梯度就很简单的。

1.3.3 DNN 反向传播算法过程

• 这里以 Batch 批量梯度下降讨论，实际上工程上一般都会采用 Mini-Batch，不过说明算法，影响不大。
• 输入：
  
  • 总层数 L，以及各隐藏层与输出层的神经元个数，激活函数，损失函数，迭代步长 α,最大迭代次数 MAX 与停止迭代阈值 ϵ，输入的 m 个训练样本。
• 输出：
  
  • 各隐藏层与输出层的线性关系系数矩阵 W 和偏倚向量 b
    
    

• 算法流程：

  • (1) 初始化各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b的值为一个随机值。
  • (2) for iter to 1 to MAX：
    
    • (2.1) for i =1 to m：
      
      • (a) 将DNN输入 $a^1$ 设置为 Xi
      • (b) for l=2 to L，进行前向传播算法计算, $a^{i,l} = \sigma(z^{i,l}) = \sigma(W^la^{i,l-1} + b^l)$
      • (c) 通过损失函数计算输出层的 $\delta^{i,L}$
      • (d) for l= L to 2, 进行反向传播算法计算 $\delta^{i,l} = (W^{l+1})^T\delta^{i,l+1}\odot \sigma^{'}(z^{i,l})$
    • (2.2) for l = 2 to L，更新第l层的 $W^l,b^l$ :
      
      • $W^l = W^l -\alpha \sum\limits_{i=1}^m \delta^{i,l}(a^{i, l-1})^T$
      • $b^l = b^l -\alpha \sum\limits_{i=1}^m \delta^{i,l}$
    • (2.3) 如果所有W，b的变化值都小于停止迭代阈值ϵ，则跳出迭代循环到步骤3
  • (3) 输出各隐藏层与输出层的线性关系系数矩阵W和偏倚向量 b

• 如果说看到这里你或许觉得，理解的不是很深刻，或者说觉得太过于理论推导，没有实际例子直观理解的话，那么这里博主便推荐您可以去学习一下这篇文章，它用形象生动的例子加以说明，我想会帮助到您的 BP 算法的理解的。用一个小例子来说明 BP 算法

1.3.4 基于 DNN 反向传播算法的思考

• 基于上面的算法推导，我们知道DNN的参数众多，矩阵运算量也很大，直接使用会有各种各样的问题。有哪些问题以及如何尝试解决这些问题并优化DNN模型与算法，当然，这些问题已经有很多科学家给出了一些解决方法或者正在探索中，而对我们来说，这也是非常值得我们去学习的一个方面，下面就简略的讨论一下这些问题，暂不做理论推导。
  
  
• 从损失函数和激活函数方面考虑：
  
  • 前面我们选用的激活函数是 Sigmoid 函数，而如最开始给出的图像可以看出，对于Sigmoid，当 z 的取值越来越大后，函数曲线变得越来越平缓，意味着此时的导数 σ′(z) 也越来越小。同样的，当 z 的取值越来越小时，也有这个问题。仅仅在z取值为 0 附近时，导数 σ′(z) 的取值较大。在前面讨论的均方差+Sigmoid的反向传播算法中，每一层向前递推都要乘以 σ′(z),得到梯度变化值。从它的函数图像曲线来看在大多数时候，我们的梯度变化值很小，导致我们的 W,b 更新到极值的速度较慢，即算法收敛速度较慢。
  • Sigmoid的函数特性导致反向传播算法收敛速度慢的问题，那么如何改进呢？换掉Sigmoid ？这当然是一种选择。另一种常见的选择是用交叉熵损失函数来代替均方差损失函数。先讨论换损失函数为交叉熵 + Sigmoid 激活函数，如下：
    $$J(W,b,a,y) = -y \bullet lna- (1-y) \bullet ln(1 -a)$$
  • 然后，我们计算，输出层$δ^L$的梯度情况,发现梯度里面居然没有有了 $\sigma ^{'}(z)$，因此即使 Sigmoid 函数两边倒数极小，也不会影响到我们的收敛速度。
    
    
  • 此外，当我们做分类问题时，通常会考虑用到 对数似然损失函数和softmax激活函数，这里不讨论为何，感兴趣的读者可自行探索 。神经元的激活函数定义如下：
    $$a_i^L = \frac{e^{z_i^L}}{\sum\limits_{j=1}^{n_L}e^{z_j^L}}$$
  • 第三个问题便是，DNN 的梯度爆炸梯度消失与ReLU激活函数问题，在 CNN 里面使用 ReLU 激活函数解决梯度消失更加常见。什么是梯度爆炸和梯度消失呢 ？ 下面，尝试用通用的语言描述一下，因为它很复杂，都可以出一大本书，故这里简要叙述。
  • 简单说来，就是在反向传播的算法过程中，由于我们使用了是矩阵求导的链式法则(如下)，有一大串连乘，如果连乘的数字在每层都是小于1的，则梯度越往前乘越小，导致梯度消失，而如果连乘的数字在每层都是大于1的，则梯度越往前乘越大，导致梯度爆炸。
    $$\delta^l =\frac{\partial J(W,b,x,y)}{\partial z^l} = \frac{\partial J(W,b,x,y)}{\partial z^L}\frac{\partial z^L}{\partial z^{L-1}}\frac{\partial z^{L-1}}{\partial z^{L-2}}...\frac{\partial z^{l+1}}{\partial z^{l}}$$
    
    
  • 一般工程上常用的有：
    
    • 而对于梯度爆炸，则一般可以通过调整我们DNN模型中的初始化参数得以解决。
      
      
    • 对于无法完美解决的梯度消失问题，一个可能部分解决梯度消失问题的办法是使用ReLU（Rectified Linear Unit）激活函数，ReLU在卷积神经网络CNN中得到了广泛的应用。它的表达式很简单，即大于等于0则不变，小于0则激活后为0。$\sigma(z) = max(0,z)$
      
      
  • 此外，为了解决过拟合问题，对于正则方面，这里就不复述常见的 L2 正则了，它即可以用于均方误差函数，也可以用于交叉熵函数。此外，可以采用集成学习(Bagging)方法正则化，但是由于参数进一步增多，一般只做5-10 个 DNN 模型。这里，我们关注一下这个，dropout 正则化，它和 Bagging 方法很类似，但是又有一些不同的地方。
    
    
  • 所谓的Dropout指的是在用前向传播算法和反向传播算法训练DNN模型时，一批数据迭代时，随机的从全连接DNN网络中去掉一部分隐藏层的神经元。在用去掉隐藏层的神经元的网络来拟合我们的一批训练数据。用这个去掉隐藏层的神经元的网络来进行一轮迭代，更新所有的W,b。总结一下，即每轮梯度下降迭代时，它需要将训练数据分成若干批，然后分批进行迭代，每批数据迭代时，需要将原始的DNN模型随机去掉部分隐藏层的神经元，用残缺的DNN模型来迭代更新W,b。每批数据迭代更新完毕后，要将残缺的DNN模型恢复成原始的DNN模型。
    
    
  • 它和 Bagging 的区别，dropout模型中的W,b是一套，共享的。所有的残缺DNN迭代时，更新的是同一组W,b；而Bagging正则化时每个DNN模型有自己独有的一套W,b参数，相互之间是独立的。当然他们每次使用基于原始数据集得到的分批的数据集来训练模型，这点是类似的。

二、基于 TensorFlow 的前向神经网络的代码实践

2.1 涉及到的 TensorFlow 库函数

• TensorFlow 的激活函数

  • tf.sigmoid(x) 标准的 Sigmoid 函数
  • tf.tanh(x) 双曲正切函数
  • tf.nn.relu(x) 修正线性函数

• TensorFlow 中的其他函数

  • tf.nn.elu(x) 指数线性单元；如果输入小于0，则返回 exp(x) -1;否则，返回 x
  • tf.softsign(x) 返回 x/ (abs(x) + 1)
  • tf.nn.bias_add(value,bias) 增加一个 bias 到 value

• Tensorflow 的一些损失优化方法

  • tf.train.GradientDescentOptimizer(learning_rate,use_locking,name) 原始梯度下降方法，唯一的参数就是学习率
  • tf.train.AdagradOptimizer 自适应调整学习率，累计历史梯度的平方作为分母，防止有些方向的梯度值过大，提高优化效率，善于处理稀疏梯度
  • tf.train.AdadeltaOptimizer 扩展的 AdaGrad 优化方法，只累计最近的梯度值，而不对整个历史上的梯度进行累加
  • tf.train.AdamOptimizer 梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率， Adam是自适应矩估计(Adaptive Moment Estimation) 的首字母缩写。
    
    

2.2 拟合非线性数据回归

# 本例中我们通过手动生成二次函数加噪声的数据集，然后通过最为简单的神经网络去拟合它，以达到学习的目的           
%matplotlib inline 
import numpy as np 
import matplotlib.pyplot as plt 
import tensorflow as tf 
from sklearn.utils import shuffle 
from sklearn.metrics import accuracy_score

# 数据集的大小定义
trainsamples = 200
testsamples = 60 

# Here we will represent the model,a simple imput, 
# a hidden layer of sigmoid activation,
# 这里定义一个输入城，一个输出层，一个有10个节点的隐层网络
def model(X,hidden_weights1,hidden_bias1,ow):
    hidden_layer = tf.nn.sigmoid(tf.matmul(X,hidden_weights1) + hidden_bias1)
    return tf.matmul(hidden_layer, ow)  

# 创建数据集  
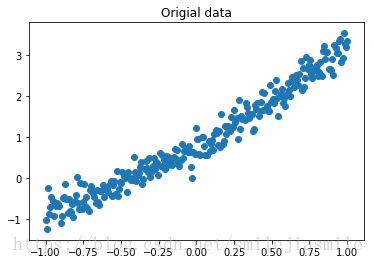
dsX = np.linspace(-1, 1, trainsamples + testsamplt).transpose()  
dsY = 0.4 * pow(dsX,2) + 2 * dsX + np.random.randn(*dsX.shape) * 0.22 + 0.8  

plt.figure()   # create a new figure  
plt.title('Origial data')
plt.scatter(dsX,dsY)  

<matplotlib.collections.PathCollection at 0x114554110>

X = tf.placeholder('float')  
Y = tf.placeholder('float')  

# create first hidden layer  
hw1 = tf.Variable(tf.random_normal([1, 10],stddev=0.01))
# create output connection 
ow = tf.Variable(tf.random_normal([10, 1],stddev=0.01))  
# create bias  
b = tf.Variable(tf.random_normal([10],stddev=0.01)) 

model_y = model(X,hw1,b,ow)

# cost Function
cost = tf.pow(model_y - Y,2) / (2)  

# create train Operator
train_op = tf.train.AdamOptimizer(0.01).minimize(cost)

# Launch the graph in a session 
with tf.Session() as sess:
    tf.initialize_all_variables().run()  

    # 开始迭代
    for i in range(1,35):
        trainX, trainY = dsX[0:trainsamples], dsY[0:trainsamples] 
        for x1, y1 in zip(trainX,trainY):
            sess.run(train_op,feed_dict={X:[[x1]],Y:y1})

        testX, testY = dsX[trainsamples:trainsamples + testsamples],dsY[trainsamples:trainsamples+testsamples]        
        # print testY
        cost1 = 0.  
        for x1, y1 in zip(testX,testY):
            cost1 += sess.run(cost,feed_dict={X: [[x1]], Y: y1}) / testsamples 


        print "Average cost for epoch" + str(i) + ':' + str(cost1)

Average cost for epoch1:[[0.26329115]]
Average cost for epoch2:[[0.22221012]]
Average cost for epoch3:[[0.14709872]]
Average cost for epoch4:[[0.10356887]]

此处省略部分内容：

Average cost for epoch29:[[0.02887413]]
Average cost for epoch30:[[0.02915836]]
Average cost for epoch31:[[0.029492]]
Average cost for epoch32:[[0.0298766]]
Average cost for epoch33:[[0.0303134]]
Average cost for epoch34:[[0.03080252]]

2.3、使用 Keras 对连续型变量进行建模

%matplotlib inline 
import pandas as pd 
import matplotlib as mpl 
import matplotlib.pyplot as plt 

from sklearn import datasets, cross_validation,metrics
from sklearn import preprocessing 

from tensorflow.contrib import learn  

from keras.models import  Sequential 
from keras.layers import  Dense  

# Read the original dataset 
data = pd.read_csv('mpg.csv',header=0)
print data.describe()
# Convert the displacement column as float 
data['displacement'] = data['displacement'].astype(float)

# 忽略第一列和最后一列  
X = data[data.columns[1:8]] 
y = data['mpg'] 

plt.figure()
f, ax1 = plt.subplots()
for i in range(1,8):
    number = 420 + i 
    ax1.locator_params(bnbins=3) 
    ax1 = plt.subplot(number)
    plt.title(list(data)[i])
    ax1.scatter(data[data.columns[i]],y)  

plt.tight_layout(pad=0.4,w_pad=0.5,h_pad=1.0)

              mpg   cylinders  displacement  horsepower       weight  \
count  398.000000  398.000000    398.000000  398.000000   398.000000   
mean    23.514573    5.454774    193.425879  102.894472  2970.424623   
std      7.815984    1.701004    104.269838   40.269544   846.841774   
min      9.000000    3.000000     68.000000    0.000000  1613.000000   
25%     17.500000    4.000000    104.250000   75.000000  2223.750000   
50%     23.000000    4.000000    148.500000   92.000000  2803.500000   
75%     29.000000    8.000000    262.000000  125.000000  3608.000000   
max     46.600000    8.000000    455.000000  230.000000  5140.000000   


<matplotlib.figure.Figure at 0x11d0fd990>

# Split the datasets 
X_train, x_test, y_train, y_test = cross_validation.train_test_split(X,y,test_size=0.25)

# Scale the data for convergency optimization 
scaler = preprocessing.StandardScaler()

# set the transform parameters 
X_train = scaler.fit_transform(X_train) 

# Build a 2 layer fully connected DNN with 10 and 5 units respectively 
model = Sequential()
model.add(Dense(10,input_dim=7,init='normal',activation='relu'))
model.add(Dense(5,init='normal',activation='relu'))
# 输出
model.add(Dense(1,init='normal'))  

# Compile the model, which the mean squared error as a loss function
model.compile(loss='mean_squared_error',optimizer='adam')

# Fit the model,in 1000 epochs 
# verbose：日志显示，0为不在标准输出流输出日志信息，1为输出进度条记录，2为每个epoch输出一行记录
# epochs：整数，训练终止时的epoch值，训练将在达到该epoch值时停止
model.fit(X_train,y_train,nb_epoch=1200,validation_split=0.33,shuffle=True,verbose=2)  

Train on 199 samples, validate on 99 samples
Epoch 1/1200
 - 0s - loss: 624.4550 - val_loss: 609.7046
Epoch 2/1200
 - 0s - loss: 624.0735 - val_loss: 609.3263
Epoch 3/1200

此处省略部分内容 ······

Epoch 1197/1200
 - 0s - loss: 6.9051 - val_loss: 8.6608
Epoch 1198/1200
 - 0s - loss: 6.9028 - val_loss: 8.6282
Epoch 1199/1200
 - 0s - loss: 6.8984 - val_loss: 8.6874
Epoch 1200/1200
 - 0s - loss: 6.8917 - val_loss: 8.8152


<keras.callbacks.History at 0x11ec65ed0>

2.4 多分类问题，多节点输出层

%matplotlib inline 
import pandas as pd 
import matplotlib.pyplot as plt 
import tensorflow as tf 
from sklearn.utils import shuffle 
from sklearn import preprocessing  

# 读取数据
data = pd.read_csv('./wine.csv',header=0)
print (data.describe())  

for i in range(1,8):
    number = 420 + i 
    ax1 = plt.subplot(number)
    ax1.locator_params(nbins=3)
    plt.title(list(data)[i])
    ax1.scatter(data[data.columns[i]],data['Wine'])  
plt.tight_layout(pad=0.4,w_pad=0.5,h_pad=1.0)

             Wine     Alcohol  Malic.acid         Ash         Acl          Mg  \
count  178.000000  178.000000  178.000000  178.000000  178.000000  178.000000   
mean     1.938202   13.000618    2.336348    2.366517   19.494944   99.741573   
std      0.775035    0.811827    1.117146    0.274344    3.339564   14.282484   
min      1.000000   11.030000    0.740000    1.360000   10.600000   70.000000   
25%      1.000000   12.362500    1.602500    2.210000   17.200000   88.000000   
50%      2.000000   13.050000    1.865000    2.360000   19.500000   98.000000   
75%      3.000000   13.677500    3.082500    2.557500   21.500000  107.000000   
max      3.000000   14.830000    5.800000    3.230000   30.000000  162.000000   

sess = tf.InteractiveSession()
X = data[data.columns[1:13]].values 

# 数据本身是从 1 开始的，为数据减去偏差，然后将 Y 映射成一位有效 (one-hot) 编码 
y = data['Wine'].values - 1 
Y = tf.one_hot(indices=y,depth=3,on_value=1.,off_value=0.,axis=1,name='a').eval()          
X, Y = shuffle(X, Y) 

# 对训练数据正则化
scaler = preprocessing.StandardScaler()
X = scaler.fit_transform(X) 

# 此处为一个隐层神经网络，旨在学习，针对模型难易度，选择合适的隐层
# Create the model， 使用 softmax 激活函数 + 相对熵为损失函数，作为多分类 
x = tf.placeholder(tf.float32,[None,12])   # 输入 x 的特征有 12 个维度
W = tf.Variable(tf.zeros([12,3]))          # 权重为 12 * 3 
b = tf.Variable(tf.zeros([3]))             # 偏置为 1 * 3 
y = tf.nn.softmax(tf.matmul(x,W) + b)  

# Define loss and optimizer ，损失函数交叉熵定义如下 ：
y_ = tf.placeholder(tf.float32,[None,3]) 
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y),reduction_indices=[1]))          
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(cross_entropy)  

# Train 
tf.initialize_all_variables().run()                 # 先初始化变量
for i in range(20):
    X, Y = shuffle(X,Y,random_state=1)              # 随机打乱数据，增加泛化能力

    Xtr = X[0:140,:]
    Ytr = Y[0:140,:] 

    Xt = X[140:178,:] 
    Yt = Y[140:178,:] 
    Xtr, Ytr = shuffle(Xtr,Ytr,random_state=0) 

    batch_xs, batch_ys = Xtr, Ytr 
    train_step.run({x:batch_xs,y_:batch_ys}) 
    cost = sess.run(cross_entropy,feed_dict={x:batch_xs,y_:batch_ys})

    # Test trained model 
    correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1)) 
    accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) 
    print(accuracy.eval({x:Xt,y_:Yt}))  

   此处省略部分东西 ······
    0.94736844
    0.94736844
    0.94736844
    0.94736844
    0.9736842
    1.0
    0.9736842

码字不易，如若对您有所帮助，请点赞以留下您的足迹，也好激励我，不断前行。

注： 本文参考引用文章如下：(在此非常感谢以下优秀的博主,让我学到了很多有用的东西)
1、 http://www.cnblogs.com/pinard/p/6472666.html
2、 https://www.jianshu.com/p/964345dddb70