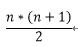一、高斯求和
1+2+3+...+100的值是多少?
1、高斯的解答
1+2+3+...+100的计算结果和100+99+98+...+1的计算结果是一样的,那么就可以将这两串数字进行纵向相加,如下:
| 1+ | 2+ | 3+ | ... | +100 | |
| + | 100+ | 99+ | 98+ | ... | +1 |
| 101+ | 101+ | 101+ | ... | +101 | |
| 有100个101 |
101*100=10100/2=5050
2、归纳
高斯使用了以下等式
如果使用变量n,将“1到100”归纳为“1到n”,这样上面的等式变为如下形式
那么这个等式对于0以上的任意整数n都成立吗?如果成立该如何证明呢?这时就需要用到数学归纳法了。
二、数学归纳法
1、0以上整数的断言
例1:
▶ 断言A(n):n×2为偶数
如果n为0,A(0)的结果是0,为偶数;
如果n为1,A(1)的结果是2,为偶数;
如果n为2,A(2)的结果是4,为偶数;
因为0以上的任意数乘以2结果都为偶数,所以对0以上的所有整数,断言A(n)为真。
例2:
▶ 断言B(n):n×3为奇数
如果n为0,B(0)的结果是0,为偶数;
如果n为1,B(1)的结果是3,为奇数;
如果n为2,B(2)的结果是6,为偶数;
n=2是推翻“断言B(n)对于0以上的所有整数n都成立”的反例。
所以断言B(n)不为真,为假。
2、高斯断言
▶ 断言G(n):0到n的整数之和为
3、什么是数学归纳法
数学归纳法是证明有关整数的断言对于0以上的所有整数是否成立时所用的方法。
假设现在要用数学归纳法来证明“断言P(n)对于0以上的所有整数n都成立”,则证明步骤如下:
● 步骤1
证明“P(0)成立”;
● 步骤2
证明n不论为0以上的哪个整数,“若P(n)成立,则P(n+1)也成立”。
在上面的证明步骤中,我们将步骤1称为基底,步骤2称为归纳。如果步骤1和步骤2都能得到证明,就证明了“断言P(n)对于0以上的所有整数n都成立”。
4、用数学归纳法证明高斯断言
● 步骤1:证明基底成立
证明G(0)成立。
G(0)就是“0到0的整数之和与0*(0+1)/2”相等;
可以直接通过计算证明,0到0的整数之和为0,0*(0+1)/2的结果也是0;
步骤1证明完毕。
● 步骤2:归纳的证明
证明n为0以上的任一整数时,“若G(n)成立,则G(n+1)也成立”。
先假设G(n)成立,这时,以下等式成立:
假设成立的等式G(n)
要证明的等式G(n+1)
现进行如下计算:
G(n+1)左边和右边的计算结果相同
由此,G(n)到G(n+1)的推导成功,步骤2得到了证明。
至此,通过数学归纳法的步骤1、步骤2都证明了G(n),也就是说通过数学归纳法证明了断言G(n)对于0以上的任意整数n都成立。