一、树状数组是干什么的?
维护数组看起来是十分简单的事情。
修改某点的值只要有下标直接就能改了,那对于求某个区间的和,似乎只能遍历一遍,复杂度是O(N),而这恰恰是树状数组的强项!
如果实时的对数组进行M次修改或求和,最坏的情况下复杂度是O(M*N),当规模增大后这是划不来的!而树状数组干同样的事复杂度却是O(M*logN),别小看这个log,很大的数一log就很小了。
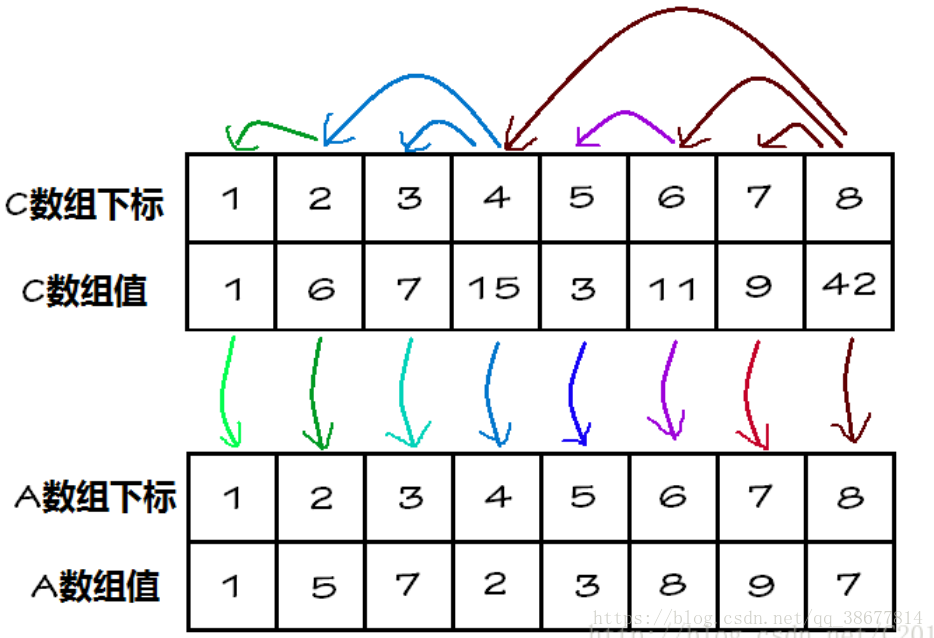
A数组是原始n个数的数组,C数组就是是树状数组(“树状”数组,是指一个普通数组,按树状存储,而不是一种STL中的数据结构)。
声明:刚开始我并不能找出什么规律
仔细找啊!!!加加减减
C[1] = A[1]
C[2] = C[1] + A[2] = A[1] + A[2]
C[3] = A[3]
C[4] = C[2] + C[3] +A[4] = A[1] + A[2] + A[3] + A[4]
C[5] = A[5]
C[6] = C[5] + A[6] = A[5] + A[6]
C[7] = A[7]
C[8] = C[4] + C[6] + C[7] + A[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
好像是有点规律,这么复杂的东西有个啥用!!!

wow!这么高级的东西
发现这个的人真的厉害(无聊!)
计算lowbit(lowbit(x)为2的k次幂,其中k为x在二进制下末尾0的个数)
呵lowb
lowbit(x)=x&-x =2^k
int lowbit(int t)
{
return t&(-t);
}
//-t 代表t的负数 计算机中负数使用对应的正数的补码来表示
//例如 :
// t=6(0110) 此时 k=1
//-t=-6=(1001+1)=(1010)
// t&(-t)=(0010)=2=2^1
C[i]=A[i-2^k+1]+A[i-2^k+2]+……A[i];
C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+……A[i];
把2^k都换成lowb
getsum操作
就是求前缀和,神奇啊
int getsum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))//i要大于0
ans+=C[i];
return ans;
}上面的函数即为区间查询
ok 下面利用C[i]数组,求A数组中前i项的和
举个例子 i=7;
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ; 前i项和
C[4]=A[1]+A[2]+A[3]+A[4]; C[6]=A[5]+A[6]; C[7]=A[7];
可以推出: sum[7]=C[4]+C[6]+C[7];
单点更新
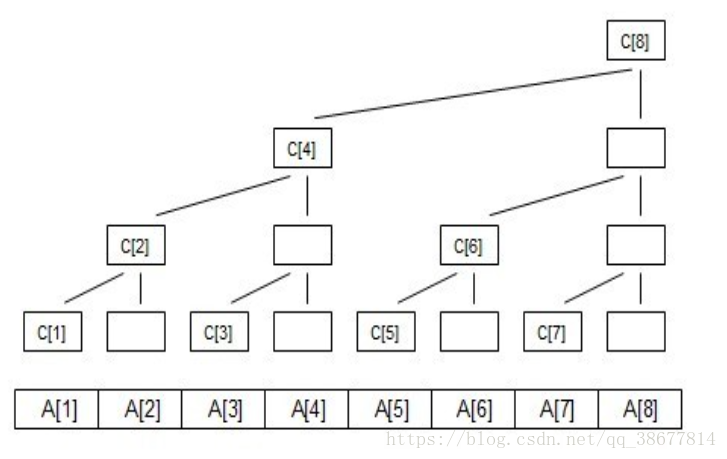
当我们修改A[]数组中的某一个值时 应当如何更新C[]数组呢?
回想一下 区间查询的过程,再看一下上文中列出的图
update操作
当要动态改变一个数时,用刚刚的循环枚举出与它相关的位置,都增加(减少)即可:
这个与他相关一定要理解好,牵一发而动全身呐
void update(int k,int x)
{
for(int i=k;i<=n;i+=lowbit(i))
C[i]+=x;
}当更新A[1]时 需要向上更新C[1] ,C[2],C[4],C[8]
C[1], C[2], C[4], C[8]
写为二进制 C[(001)],C[(010)],C[(100)],C[(1000)]
1(001) C[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]
区间修改
树状数组升级版本
比如需要将x到y中每个数加上100
暴力O(N)
怎么做呢
想想看
…
int i 循环x到y update(i,100) !!
那我要你树状数组何用???
但说明你已经开始掌握精髓了
引入一个概念 非常重要
差分
设数组a[]={1,6,8,5,10},那么差分数组b[]={1,5,2,-3,5}
也就是说b[i]=a[i]-a[i-1];(a[0]=0;),那么a[i]=b[1]+….+b[i];(这个很好证的)。
假如区间[2,4]都加上2的话
a数组变为a[]={1,8,10,7,10},b数组变为b={1,7,2,-3,3};
发现了没有,b数组只有b[2]和b[5]变了,因为区间[2,4]是同时加上2的,所以在区间内b[i]-b[i-1]是不变的.
所以对区间[x,y]进行修改,只用修改b[x]与b[y+1]:
b[x]=b[x]+k;b[y+1]=b[y+1]-k;
好了
引入例题
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数数加上x
2.求出某一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含2或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x 含义:输出第x个数的值
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例#1: 复制
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
输出样例#1: 复制
6
10
#include <bits/stdc++.h>
using namespace std;
#define lowbit(i) i&(-i)
int a[1000000];
int tree[1000000];
int N,M;
int getsum(int x){
int sum=0;
for(int i=x;i;i-=lowbit(i)){
sum+=tree[i];
}
return sum;
}
void insert(int x,int val){
for(int i=x;i<=N;i+=lowbit(i)){
tree[i]+=val;
}
}
void update(int l,int r,int val){
insert(l,val);//单点修改
insert(r+1,-val);//单点修改
}
int main(){
cin>>N>>M;
for(int i=1;i<=N;i++){
cin>>a[i];
insert(i,a[i]-a[i-1]);//对差分数组构建树状数组
}
for(int i=1;i<=M;i++){
int a,b,c,d;
cin>>a;
if(a==1){
cin>>b>>c>>d;
update(b,c,d);//b到c全部加d
}
else{
cin>>b;
printf("%d\n",getsum(b));
}
}
return 0;
}升级版的树状数组需要区间求和呢?
我们需要额外一个数组来帮助我们~
举例
a[1]=tree[1]
a[2]=tree[1]+tree[2]
a[3]=tree[1]+tree[2]+tree[3]
a[4]=tree[1]+tree[2]+tree[3]+tree[4]
那么类似的
a[1]+a[2]+……+a[r-1]+a[r]
//用上方公式推导得出
=tree[1]+(tree[1]+tree[2])+……+(tree[1]+……+tree[r])
//根据加法交换律与结合律:
=(tree[1]*(r))+(tree[2]*(r-1))+……(tree[r]*1)
//那么:
=r*(tree[1]+tree[2]+……+tree[r])-(tree[1]*0+tree[2]*1+……+tree[r]*(r-1))你看r*(一坨)可以用我们的升级版树状数组做,后面的那个规律也很明显
tree1[i]=tree[i]*(i-1)对吧!
好了
只要针对这个修改一下代码即可
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例#1: 复制
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
输出样例#1: 复制
11
8
20
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(i) i&(-i)
ll n,m;
ll tree[100010]={0};
ll tree1[100010]={0};
ll getsum(ll *array,ll x){
ll sum=0;
for(int i=x;i;i-=lowbit(i)){
sum+=array[i];
}
return sum;
}
void insert(ll *array,ll index,ll val){
for(ll i=index;i<=n;i+=lowbit(i)){
array[i]+=val;
}
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m;
ll a,b=0;
for(ll i=1;i<=n;i++){
cin>>a;
b=a-b;//差分思想
insert(tree,i,b);
insert(tree1,i,b*(i-1));
b=a;
}
for(ll i=1;i<=m;i++){
int t,x,y,z;
cin>>t;
if(t==1){
cin>>x>>y>>z;
insert(tree,x,z);
insert(tree,y+1,-z);
insert(tree1,x,z*(x-1));
insert(tree1,y+1,-z*(y));
}
else{
cin>>x>>y;
cout<<getsum(tree,y)*y-(x-1)*getsum(tree,x-1)-(getsum(tree1,y)-getsum(tree1,x-1))<<endl;
}
}
return 0;
}