十一行Python代码实现一个误差逆传播（BP）神经网络

标签（空格分隔）： BP 神经网络机器学习

通过一个例子，来学习BP神经网络。这个例子来源于十一行Python代码实现一个神经网络（第一部分），好像也是翻译别人的博客。算法的推导来自周志华的《机器学习》。

样本定义

假设训练样本如下：

输入1	输入2	输入3	输出
0	0	1	0
1	1	1	1
1	0	1	1
0	1	1	0

这是一个拥有3个输入节点1个输出节点，总共4个样例的训练样本。所以，可以画出下图这样的两层神经网络图，y点为输出节点， $x_1$ , $x_2$ , $x_3$ 为输入节点。 $\omega_1$ , $\omega_2$ , $\omega_3$ 为各个节点的权值。
BP.png-5.2kB
根据《机器学习》（周志华的西瓜书）记述，可以设输出节点 $y$ 的激励函数为Sigmoid函数：

s i g m o i d (x) = 1 1 + e - x

$sigmoid(x)=\frac{1}{1+e^{-x}}$
输出节点的输出值是

y=f(∑i=3i=1ωixi−θ) $y=f(\sum_{i=1}^{i=3}\omega_ix_i-\theta)$ 。

θ $\theta$ 是该节点的阈值，即大于阈值

θ $\theta$ 时，输出1，小于时输出0。

模型推导

因为BP神经网络是通过输出节点输出值与实际值比较，每次得到的误差推导出输入节点的权值 $\omega_i$ ，即每次 $\omega_i=\omega_i+ \Delta\omega_i$
模型其他参数都是已知量（初始权重为任意假设给定值，阈值 $\theta$ 也可以看成是定值），所以，模型的关键是求出 $\omega_i$ 每次需要的改变量 $\Delta\omega_i$
根据周志华的《机器学习》P99页论述， $\Delta\omega_i=\eta(y-\hat{y})x_i$ （后面将给出证明）。其中 $\eta\in(0,1)$ 称为学习率（learning rate），用来调节 $\Delta\omega_i$ 的变化速度，可以看成是常值； $\hat{y}$ 是 $L_2$ 层节点输出值。
$\Delta\omega_i$ 的设定和PID算法有点像
这个两层神经网络的均方误差为 $E=\frac{1}{2}(\hat{y}^k-y^k)^2$ ，用梯度下降法，求出 $\Delta\omega_i$

Δ ω i = - η \partial E \partial ω i

$\Delta\omega_i=-\eta\frac{\partial{E}}{\partial{\omega_i}}$
其中，设

∑ωixi−θ=z $\sum{\omega_i}x_i-\theta=z$

\partial E \partial ω i = \partial E \partial y ^ k \cdot \partial y ^ k \partial z \cdot \partial z ω i

$\frac{\partial{E}}{\partial{\omega_i}}=\frac{\partial{E}}{\partial{\hat{y}^k}}\cdot\frac{\partial{\hat{y}^k}}{\partial{z}}\cdot\frac{\partial z}{\omega_i}$
根据sigmoid函数的性质，

f′(z)=f(z)(1−f(z)) $f'(z)=f(z)(1-f(z))$ ,可以得出

\partial y ^ k ( z ) \partial z = y^k (z) \cdot (1 - y^k (z))

$\frac{\partial{\hat{y}^k(z)}}{\partial{z}}=\hat{y}^k(z)\cdot(1-\hat{y}^k(z))$ 所以，

\partial E \partial ω i = \partial E \partial y ^ k \cdot \partial y ^ k \partial z \cdot \partial z \partial ω i = (y^k - y k) \cdot y^k \cdot (1 - y^k) \cdot x i

$\frac{\partial{E}}{\partial{\omega_i}}=\frac{\partial{E}}{\partial{\hat{y}^k}}\cdot\frac{\partial{\hat{y}^k}}{\partial{z}}\cdot\frac{\partial{z}}{\partial{\omega_i}}=(\hat{y}^k-y^k)\cdot \hat{y}^k\cdot(1-\hat{y}^k)\cdot x_i$
每次改变的

Δωi=−η⋅(y^k−yk)⋅(yk)′⋅xi=η⋅(yk−y^k)⋅y^k⋅(1−y^k)⋅xi $\Delta\omega_i=-\eta\cdot(\hat{y}^k-y^k)\cdot({y}^k)'\cdot x_i=\eta\cdot(y^k-\hat{y}^k)\cdot\hat{y}^k\cdot(1-\hat{y}^k)\cdot x_i$ ，因为要求误差最小值，所以选用梯度的反方向。

python编程

import numpy as np 
# sigmoid function 定义激活函数sigmoid（x），nonlin(x,True)就是计算sigmoid的导数。 
def nonlin(x,deriv=False):  
    if(deriv==True):  
        return x*(1-x)  
    return 1/(1+np.exp(-x))  
#生成样本训练模型，输入4*3矩阵，4个样本，每个样本3个输入值。
X = np.array([ [0,0,1],
               [1,1,1],
               [1,0,1],
               [0,1,1] ])  
#生成输出节点数值，输入4*1矩阵，4个样本，每个样本1个输出值。
y = np.array([[0,1,1,0]]).T 
#设置随机种子，这个主要是为了每次生成的随机量一样，可以使程序重复试验。
np.random.seed(1) 
#设置第一层各输入点权重，权重是随机生成的，均值是0
syn0 = 2*np.random.random((3,1)) - 1  
for iter in xrange(10000):  
    # forward propagation   l0是第一层
    l0 = X  
    # l1是输出量\hat{y},l0是输入量，与权值相乘作为输出节点激励函数的自变量
    l1 = nonlin(np.dot(l0,syn0))  
    # how much did we miss?  
    l1_error = y - l1  
    l1_delta = l1_error * nonlin(l1,True)  

    # update weights  
    syn0 += np.dot(l0.T,l1_delta)  

print "Output After Training:"  
print l1

程序解读

l0是神经网络第一层，即输入层

l0 = X

l1是输出量 $\hat{y}$ ,nonlin(np.dot(l0,syn0))是输入量l0与权值syn0相乘作为输出节点激励函数的自变量，即 $\hat{y}=l1=sigmoid(l0*syn0)=sigmoid(\sum{x_i\cdot\omega_i})$

l1 = nonlin(np.dot(l0,syn0))

计算误差 ${l1\_error} = y-\hat{y}$

l1_error = y - l1

利用梯度下降法，计算权重改变量。l1作为输出量，nonlin(l1,True)表示对输出量求导即 $nonlin(l1,True)=f'=f(1-f)=(y^k)'$
$l1\_delta=(y-\hat{y})\cdot (y^k)'$

l1_delta = l1_error * nonlin(l1,True)

对权重进行更新 np.dot(l0.T,l1_delta) 为 $l0.T\cdot l1\_delta=(y-\hat{y})\cdot (y^k)'\cdot x=\Delta\omega$ ，通过 $syn0 +=\Delta\omega$ 完成权重的更新。

syn0 += np.dot(l0.T,l1_delta)

在10000次训练之后，syn0为更新后的权重，则算出的l1为训练后输出值。

运行结果

通过10000次训练，获得权重syn0，在此权重下，输出节点的输出值：
[[ 0.00966449]
[ 0.99211957]
[ 0.99358898]
[ 0.00786506]]
误差为：
[[-0.00966449]
[ 0.00788043]
[ 0.00641102]
[-0.00786506]]
通过100000次训练，获得权重syn0，在此权重下，输出节点的输出值：
[[ 0.00301758]
[ 0.99753723]
[ 0.99799161]
[ 0.00246109]]
误差为：
[[-0.00301758]
[ 0.00246277]
[ 0.00200839]
[-0.00246109]]
可以发现，随着训练步骤的增多，误差越来越小。

三层神经网络

还是刚才的例子，我们这次假定网络有三层，即输入层l0，隐藏层l1，输出层l2，建立如下图的神经网络结构：
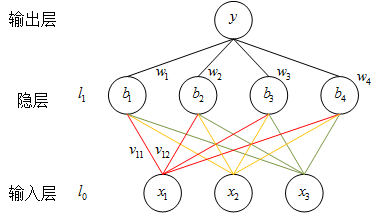
三层神经网络图
图中隐层节点 $b_i$ 到输出点 $y$ 的权重是 $\omega_i$ ，输入层节点 $x_i$ 到隐层节点 $b_j$ 的权重为 $v_{ij}$
网络在输出节点的均方误差为：

E = 1 2 (y^- y) 2

$E=\frac{1}{2}(\hat{y}-y)^2$
对其求导，得到：

\partial E \partial ω i = \partial E \partial y ^\cdot \partial y ^ \partial z \cdot \partial z \partial ω i

$\frac{\partial{E}}{\partial\omega_i}=\frac{\partial{E}}{\partial\hat{y}}\cdot\frac{\partial{\hat{y}}}{\partial z}\cdot\frac{\partial{z}}{\partial \omega_i}$
设

z=∑4j=1(ωi⋅bi−θ) $z=\sum_{j=1}^{4}(\omega_i\cdot b_i-\theta)$ ，则均方误差中，

∂E∂y^=y^−y $\frac{\partial{E}}{\partial\hat{y}}=\hat{y}-y$ ，

∂y^∂z=y^⋅(1−y^) $\frac{\partial{\hat{y}}}{\partial z}=\hat{y}\cdot(1-\hat{y})$ ，

∂z∂ωi=bi $\frac{\partial{z}}{\partial \omega_i}=b_i$ 。所以

\partial E \partial ω i = (y^- y) \cdot y^\cdot (1 - y^) \cdot b i

$\frac{\partial{E}}{\partial\omega_i}=(\hat{y}-y)\cdot \hat{y}\cdot(1-\hat{y})\cdot b_i$
因为是梯度下降，要减小误差，因此

Δωi $\Delta\omega_i$ 应该沿梯度方向相反方向前进。
所以，

Δωi=−η⋅(y^−y)⋅y^⋅(1−y^)⋅bi=η⋅(y−y^)⋅y^⋅(1−y^)⋅bi $\Delta\omega_i=-\eta\cdot (\hat{y}-y)\cdot \hat{y}\cdot(1-\hat{y})\cdot b_i=\eta\cdot (y-\hat{y})\cdot \hat{y}\cdot(1-\hat{y})\cdot b_i$
我们求得隐层到输出层的权值，现在要求输入层到隐层的权值

vij $v_{ij}$ 改变。

\partial E \partial v i j = \partial E \partial y ^\cdot \partial y ^ \partial z \cdot \partial z \partial b j \cdot \partial b j \partial α \cdot \partial α \partial v i j

$\frac{\partial E}{\partial v_{ij}}=\frac{\partial E}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial{z}}\cdot \frac{\partial z}{\partial{b_j}}\cdot \frac{\partial {b_j}}{\partial{\alpha}}\cdot\frac{\partial{\alpha}}{\partial{v_{ij}}}$
其中，

bj=f(∑3i=1vijxi−θj) $b_j=f(\sum_{i=1}^{3}v_{ij}x_i-\theta_j)$ ，

α=∑3i=1vij(xi−θj) $\alpha=\sum_{i=1}^{3}v_{ij}(x_i-\theta_{j})$
所以，

\partial E \partial v i j = (y^- y) \cdot y^\cdot (1 - y^) \cdot ω j \cdot b j \cdot (1 - b j) \cdot x i

$\frac{\partial E}{\partial v_{ij}}=(\hat{y}-y)\cdot\hat{y}\cdot(1-\hat{y})\cdot\omega_j\cdot b_j\cdot(1-b_j)\cdot x_i$
第一层节点权重的该变量

Δvij=−η∂E∂vij=−η∂E∂vij $\Delta v_{ij}=-\eta\frac{\partial E}{\partial v_{ij}}=-\eta\frac{\partial E}{\partial v_{ij}}$
假设

η=1 $\eta=1$ ，则可以得到

Δ v i j = Δ ω i \cdot ω j \cdot (1 - b j) \cdot x i

$\Delta v_{ij}=\Delta\omega_i\cdot\omega_j\cdot(1-b_j)\cdot x_i$

Δωi=−⋅(y^−y)⋅y^⋅(1−y^)⋅bi=(y−y^)⋅y^⋅(1−y^)⋅bi $\Delta\omega_i=-\cdot (\hat{y}-y)\cdot \hat{y}\cdot(1-\hat{y})\cdot b_i=(y-\hat{y})\cdot \hat{y}\cdot(1-\hat{y})\cdot b_i$

import numpy as np

def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)
    return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
              [0,1,1],
              [1,0,1],
              [1,1,1]])
y = np.array([[0],
              [1],
              [1],
              [0]])
np.random.seed(1)
# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1

for j in range(60000):
    # Feed forward through layers 0, 1, and 2
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))#计算隐层节点的输出值
    l2 = nonlin(np.dot(l1,syn1))#计算输出节点输出值
    # how much did we miss the target value?
    l2_error = y - l2   #计算输出与实际值误差

    if (j% 10000) == 0:
        print("Error:" + str(np.mean(np.abs(l2_error))))
    # in what direction is the target value?
    # were we really sure? if so, don't change too much.
    l2_delta = l2_error*nonlin(l2,deriv=True)

    # how much did each l1 value contribute to the l2 error (according to the weights)?
    l1_error = l2_delta.dot(syn1.T)

    # in what direction is the target l1?
    # were we really sure? if so, don't change too much.
    l1_delta = l1_error * nonlin(l1,deriv=True)
    syn1 += l1.T.dot(l2_delta)
    syn0 += l0.T.dot(l1_delta)

程序解读

三层神经网络与二层相似，增加了隐层后需要计算隐层节点的误差，即程序35行
l1_error = l2_delta.dot(syn1.T)
l2_delta=l2_error*nonlin(l2,deriv=True)，这步计算了隐层到输出层节点的权重调节值。即理论推导中的 $\Delta\omega_i=\eta\cdot (y-\hat{y})\cdot \hat{y}\cdot(1-\hat{y})\cdot b_i$ ，假设学习率 $\eta=1$ 。
这里公式符号跟编程代码的对应关系如下（因为编码中使用的是向量或者矩阵，这里只是简单的列出对应关系。）

公式符号	代码	公式符号	代码
$y-\hat{y}$	l2_error	$b_j$	l1
$\hat{y}$	l2	$\hat{y}(1-\hat{y})$	nonlin(l2,deriv=True)
$\Delta\omega_i=(y-\hat{y})\hat{y}(1-\hat{y})b_i$	l1.T.dot(l2_delta)	$(y-\hat{y})\hat{y}(1-\hat{y})$	l2_delta
$(y-\hat{y})\hat{y}(1-\hat{y})\omega_j$	l1_error	$(y-\hat{y})\hat{y}(1-\hat{y})\omega_jb_j(1-b_j)$	l1_delta
$\Delta v_{ij}=(y-\hat{y})\hat{y}(1-\hat{y})\omega_jb_j(1-b_j)x_i$	l0.T.dot(l1_delta)	$x_i$	l0.T

通过对应关系表，可以读懂程序中每一步代码的含义。

后记

神经网络是建立输入和输出之间的映射关系，如果输入是一张猫的照片，输出结果则为猫。
绝大多数时候，我们不能建立线性映射关系，建立映射关系需要复杂的函数，神经网络可以以任意精度逼近任一连续可微函数（这个是被证明过得），因此只要层数、神经元够多，我们就能建立关系，但是复杂性会随之增加。机器学习就是通过各种关系，来建立这一关系。

参考

神经网络之BP神经网络（Python实现）：主要是公式推导
一个 11 行 Python 代码实现的神经网络:本文代码的主要参考
周志华的《机器学习》：本文公式推导的参考来源