一、什么是神经网络NN

二、数学原理

正向传播

误差逆传播BP

一、什么是神经网络NN

神经网络（neural networks）是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。

神经网络中最基本的成分是神经元，即上述定义中的“简单单元”，在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个“阈值”，那么他就会被激活，即“兴奋”起来，想其他神经元发送化学物质。

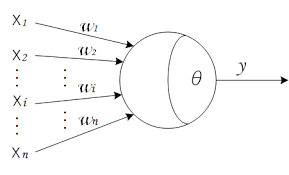
上述情形，在1943年，就被抽象成了“M-P神经元模型”（上图）。在这个模型中，神经元接受来自n个其他神经元，通过带权重的连接传递过来的信号；神经元将接受到的总输入值与神经元的阈值进行比较，然后通过“激活函数”处理并输出神经元的处理结果，较常用的激活函数为：

$sigmoid(x) = \frac {1}{1 + e^{-x}}$

他的图像为：

File:Sigmoid-function-2.svg

将M-P模型进行扩展，由一个神经元，扩展到多层多个神经元，就是神经网络了。下图为深度神经网络（DNN）示意图

那这样扩展之后，要如何给每个神经元输入数据，每个神经元又是如何计算出输出值，又如何使得结果更加准确呢，这就涉及到了数学原理相关的推导

二、数学原理

正向传播

假设我们有一个神经网络如下：

从上图可以很容易看出，第h个隐层的输入，和第j个输出层的输入，是下记两个求和公式：

$\\\alpha _{h} = \sum _{i = 1}^{k}v_{ih}x_{i}\\ \beta _{j} = \sum _{h = 1}^{q}w_{hj}b_{h}$

如果我们都有sigmoid作为激活函数：

$f(x) = \frac {1}{1 + e^{-x}}$

此处先额外证明一下此公式的一个特性： $f'(x) = f(x)(1 - f(x))$

$f'(x) = -1 \cdot (1 + e^{-x})^{-2} \cdot -1 \cdot e^{-x} \\\\= \frac {e^{-x}}{(1 + e^{-x})^{2}} \\\\= \frac {1}{1 + e^{-x}} \cdot \frac {e^{-x}}{1 + e^{-x}} \\\\= \frac {1}{1 + e^{-x}} \cdot \frac {1 + e^{-x} - 1}{1 + e^{-x}} \\\\= \frac {1}{1 + e^{-x}} \cdot (1 - \frac {1}{1 + e^{-x}}) \\\\= f(x) \cdot (1 - f(x))$

那我们的隐层和输出层的输出与输入的关系，使用激活表达式的表达结果如下：

$\\\hat{y} = f(\beta _{j} - \theta _j)\\ b_{h} = f(\alpha _{h} - \gamma _{h})$

使用上述的几个式子，就可以获得从输入层的输入，到输出层输出的所有正向过程了

但是其中有几个值，是无法真实获得，需要随机初始化的变量：

输入层和隐层的连接权 $v_{ih}$

隐层的阈值 $\gamma _{h}$

隐层和输出层的连接权 $w_{hj}$

输出层的阈值 $\theta _{j}$

为了使得NN达到更好的效果，我们希望上面的4个值最终调整到比较合理的值

那么如何调整这些值呢，就需要用到误差逆传播BP的推导了

误差逆传播BP

BP的主体思想为：从误差曲线上任意一点开始，如果想要找到这条曲线的最小值，使得误差最小，最快的方向为当前位置导数的逆方向

比如 $y = x^{2}$ 的曲线如下：

蓝色的点为我们开始的点（即随机了连接权以及阈值之后，首次计算获得的误差）红色的线为当前的切线

如果我们想从蓝色的点，沿着函数曲线快速的找到函数的最小值，那一定就是沿着切线，向反方向查找（按照上图，正方向为右上，反方向为左下），是速度是最快的。BP的思路，大体就是这个思路（另外的一个思路参考牛顿迭代，也是求导，但是方式略微有不同的地方），所以我们每次对每个变量的更新公式如下：

$v_{ih} = v_{ih} + \Delta v_{ih}$

$\gamma _{h} = \gamma _{h} + \Delta \gamma _{h}$

$w_{hj} = w_{hj} + \Delta w_{hj}$

$\theta _{j} = \theta _{j} + \Delta \theta _{j}$

下面我们来推导如何求得这个导数，以及每次对每个变量调整的值应该为多少

从上述式子中，我们可以知道整体的均方差（也就是误差）为：

$E_{k} = \frac {1}{2}\sum _{j = 1}^{l}(\hat{y}_{j}^{k} - y_{j}^{k})^{2}$

输出层相关推导

先已输出层为例，和输出层相关变量的调整值为：

$\Delta w_{ih} = -\frac{\partial E_{k} }{\partial w_{hj}}$

$\Delta \theta _{j} = -\frac{\partial E_{k}}{\partial \theta _{j}}$

ps. 正常情况下，前面还要乘一个学习率 $\eta$ 来调整每次的步长；此步长一般为经验值常量，因为懒，所以此处及后面都省略不写了。但是在最终结论中，会在表达式中添加上这个值

先已连接权为例，从当前已列出的式子中，貌似看不出 $E_{k}$ 和 $w_{hj}$ 的关系，但是没有关系，我们把上述式子一步一步带入，可以获得下面的式子：

本次推导主要用到的公式如下：

$E_{k} = \frac {1}{2}\sum _{j = 1}^{l}(\hat{y}_{j}^{k} - y_{j}^{k})^{2}$

$\beta _{j} = \sum _{h = 1}^{q}w_{hj}b_{h}$

$\hat{y} = f(\beta _{j} - \theta _j)$

$f(x) = \frac {1}{1 + e^{-x}}$

将下面3个式子，一步步带入到第一个式子中，可以获得：

$E_{k} = \frac {1}{2}\sum _{j = 1}^{l}(\hat{y}_{j}^{k} - y_{j}^{k})^{2} = \frac {1}{2}\sum _{j = 1}^{l}(f(\beta _{j} - \theta _j) - y_{j}^{k})^{2} = \frac {1}{2}\sum _{j = 1}^{l}(\frac {1}{1 + e^{-(\beta _{j} - \theta _{j})}})$

从上面这个式子可以看出， $E_{k}$ 是和 $\hat {y}_{j}^{k}$ 产生关联， $\hat {y}_{j}^{k}$ 和 $\beta _{j}$ 产生关联，而在 $\beta _{j}$ 表达式中，是有 $w_{hj}$ 的，这样子就能直观看到 $E_{k}$ 和 $w_{hj}$ 是如何关联上的。现在我们想求得 $w_{hj}$ 的偏导，根据链式法则，我们可以得到下面的式子：

$\Delta w_{ih} = -\frac{\partial E_{k} }{\partial w_{hj}} = - \frac {\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac {\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} \cdot \frac {\partial \beta _{j}}{\partial w_{hj}}$

分开对每个式子求导过程如下：

$\frac {\partial E_{k}}{\partial \hat{y}_{j}^{k}} = \frac {\partial}{\partial \hat{y}_{j}^{k}}(\frac {1}{2}\sum _{j = 1}^{l}(\hat {y}_{j}^{k} - y_{j}^{k})^{2}) = \frac {1}{2} \cdot 2 \cdot (\hat {y}_{j}^{k} - y_{j}^{k}) = \hat {y}_{j}^{k} - y_{j}^{k}$

根据上面推导的sigmoid求导性质可得：

$\frac {\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} = f(\beta _{j} - \theta _{j})(1 - f(\beta _{j} - \theta _{j})) = \hat{y}_{j}^{k}(1 - \hat{y}_{j}^{k})$

$\frac {\partial \beta _{j}}{\partial w_{hj}} = \frac {\partial}{\partial w_{hj}}(\sum _{h = 1}^{q}w_{hj}b_{h}) = b_{h}$

将这3个式子带入到原式子可得：

$\Delta w_{ih} =-(\hat {y}_{j}^{k} - y_{j}^{k}) \cdot \hat{y}_{j}^{k}(1 - \hat{y}_{j}^{k}) \cdot b_{h} = (1 - \hat{y}_{j}^{k}) \cdot ({y}_{j}^{k} - \hat y_{j}^{k}) \cdot \hat y_{j}^{k} \cdot b_{h}$

等式右边的值均为已知值，可直接使用求得 $\Delta w_{ih}$

求 $\Delta \theta _{j}$ ：

$\Delta \theta_{ih} = -\frac{\partial E_{k} }{\partial w_{hj}} = - \frac {\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac {\partial \hat{y}_{j}^{k}}{\partial \theta_{j}}$

$\frac {\partial E_{k}}{\partial \hat{y}_{j}^{k}} = \frac {\partial}{\partial \hat{y}_{j}^{k}}(\frac {1}{2}\sum _{j = 1}^{l}(\hat {y}_{j}^{k} - y_{j}^{k})^{2}) = \frac {1}{2} \cdot 2 \cdot (\hat {y}_{j}^{k} - y_{j}^{k}) = \hat {y}_{j}^{k} - y_{j}^{k}$

$\frac {\partial \hat{y}_{j}^{k}}{\partial \theta_{j}} = -f(\beta _{j} - \theta _{j})(1 - f(\beta _{j} - \theta _{j})) = -\hat{y}_{j}^{k}(1 - \hat{y}_{j}^{k})$

$\therefore \Delta \theta_{ih} = -(\hat {y}_{j}^{k} - y_{j}^{k}) \cdot -\hat {y}_{j}^{k} (1 - \hat {y}_{j}^{k}) =-(1 - \hat{y}_{j}^{k}) \cdot ({y}_{j}^{k} - \hat y_{j}^{k}) \cdot \hat y_{j}^{k}$

为了表述简单，提取两者的公共部分，令 $g_{j} =(1 - \hat{y}_{j}^{k}) \cdot ({y}_{j}^{k} - \hat y_{j}^{k}) \cdot \hat y_{j}^{k}$ ，上述两者可以简化表达式为：

$\Delta w_{ih} = g_{j} \cdot b_{h}$

$\Delta \theta_{ih} = -g_{j}$

隐层相关推导

接下来求隐层相关的：

$\Delta v_{ih} = -\frac{\partial E_{k} }{\partial v_{hj}}$

$\Delta \gamma _{j} = -\frac{\partial E_{k}}{\partial \gamma _{j}}$

使用到的公式有（部分为上面推导出的结果）：

$\alpha _{h} = \sum _{i = 1}^{k}v_{ih}x_{i}$

$E_{k} = \frac {1}{2}\sum _{j = 1}^{l}(\hat{y}_{j}^{k} - y_{j}^{k})^{2}$

$f(x) = \frac {1}{1 + e^{-x}}$

$b_{h} = f(\alpha _{h} - \gamma _{h})$

$\beta _{j} = \sum _{h = 1}^{q}w_{hj}b_{h}$

$\frac {\partial E_{k}}{\partial \hat{y}_{j}^{k}} = \hat {y}_{j}^{k} - y_{j}^{k}$

$\frac {\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} = \hat{y}_{j}^{k}(1 - \hat{y}_{j}^{k})$

$g_{j} =(1 - \hat{y}_{j}^{k}) \cdot ({y}_{j}^{k} - \hat y_{j}^{k}) \cdot \hat y_{j}^{k}$

求 $\Delta v_{ih}$ ：

从上面 $E_{k}$ 和 $w_{hj}$ 的关联推导看， $E_{k}$ 和 $\beta _{j}$ 相关

从 $\beta _{j}$ 的表达式上， $\beta _{j}$ 和 $b_{h}$ 是相关的

$b_{h}$ 是隐层的输出，通过激活函数， $b_{h}$ 和隐层的输入 $\alpha _{h}$ 和阈值 $\gamma _{h}$ 相关： $b_{h} = f(\alpha _{h} - \gamma _{h})$

$\alpha _{h}$ 又和 $v_{ih}$ 相关

继续根据链式法则： $\Delta v_{ih} = -\frac {\partial E_{k}}{\partial v_{ih}} = - \frac {\partial E_{k}}{\partial b_{h}} \cdot \frac {\partial b_{h}}{\partial \alpha _{h}} \cdot \frac {\partial \alpha_{h}}{\partial v _{ih}}$

对每一项分开求导：

$\frac {\partial b_{h}}{\partial \alpha _{h}} = f(\alpha _{h} - \gamma _{h})\cdot (1 - f(\alpha _{h} - \gamma _{h})) = b_{h}(1 - b_{h})$

$\frac {\partial \alpha_{h}}{\partial v _{ih}} = \frac {\partial }{\partial v_{ih}}(\sum _{i = 1}^{d}v_{ih}x_{i}) = x_{i}$

因为一个隐层的输出，会给到多个输出层，所以在对 $b_{h}$ 求导时，需要添加一个求和：

$\frac {\partial E_{k}}{\partial b_{h}} = \sum _{j = 1}^{l}\frac {\partial E_{k}}{\partial \beta _{j}} \cdot \frac {\partial \beta _{j}}{\partial b_{h}}$

继续分开求导得：

$\frac {\partial \beta _{j}}{\partial b_{h}} = \frac {\partial}{\partial b_{h}}(\sum _{h = 1}^{q}w_{hj}b_{h}) = w_{hj}$

$\frac {\partial E_{k}}{\partial \beta _{j}} =\frac {\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac {\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} = (\hat {y}_{j}^{k} - y_{j}^{k}) \cdot \hat{y}_{j}^{k}(1 - \hat{y}_{j}^{k}) = -(1 - \hat{y}_{j}^{k}) \cdot ({y}_{j}^{k} - \hat y_{j}^{k}) \cdot \hat y_{j}^{k} = -g_{j}$

$\therefore \frac {\partial E_{k}}{\partial b_{h}} = \sum _{j= 1}^{l}\frac {\partial E_{k}}{\partial \beta _{j}} \cdot \frac {\partial \beta _{j}}{\partial b_{h}} =\sum _{j = 1}^{l} -g_{j}w_{hj}$

带入最初的式子得：

$\Delta v_{ih} = -\sum _{j = 1}^{l} -g_{j}w_{hj} \cdot b_{h}(1 - b_{h}) \cdot x_{i} = \sum _{j = 1}^{l} g_{j}w_{hj} \cdot b_{h}(1 - b_{h}) \cdot x_{i}$

令 $e_{h} =\sum _{j = 1}^{l} g_{j}w_{hj} \cdot b_{h}(1 - b_{h})$ 可得： $\Delta v_{ih} = e_{h}x_{i}$

求 $\Delta \gamma _{j}$ ：

$\Delta v_{ih} = -\frac {\partial E_{k}}{\partial v_{ih}} = - \frac {\partial E_{k}}{\partial b_{h}} \cdot \frac {\partial b_{h}}{\partial \gamma _{h}}$

$\frac {\partial E_{k}}{\partial b_{h}} = \sum _{j= 1}^{l}\frac {\partial E_{k}}{\partial \beta _{j}} \cdot \frac {\partial \beta _{j}}{\partial b_{h}} =\sum _{j = 1}^{l} -g_{j}w_{hj}$

$\frac {\partial b_{h}}{\partial \gamma _{h}} = -f(\alpha _{h} - \gamma _{h})\cdot (1 - f(\alpha _{h} - \gamma _{h})) = -b_{h}(1 - b_{h})$

$\Delta v_{ih} =-\sum _{j = 1}^{l} -g_{j}w_{hj} \cdot -b_{h}(1 - b_{h}) = -\sum _{j = 1}^{l} g_{j}w_{hj} \cdot b_{h}(1 - b_{h}) = -e_{h}$

三、结论

$\Delta w_{ih} = \eta g_{j}b_{h}$

$\Delta \theta_{ih} = -\eta g_{j}$

$\Delta v_{ih} = \eta e_{h}x_{i}$

$\Delta v_{ih} = -\eta e_{h}$

其中：

$g_{j} =(1 - \hat{y}_{j}^{k}) \cdot ({y}_{j}^{k} - \hat y_{j}^{k}) \cdot \hat y_{j}^{k}$

$e_{h} =\sum _{j = 1}^{l} g_{j}w_{hj} \cdot b_{h}(1 - b_{h})$