目录
1.旅行商问题(TSP)
旅行商问题是一个经典的组合优化问题,其目标是找到访问一系列城市并返回起点的最短可能路线。假设有(n)个城市,每两个城市之间的距离是已知的。我们定义(d_{ij})为从城市(i)到城市(j)的距离,其中(i, j = 1, 2, ..., n),并且(d_{ij} = d_{ji}),(d_{ii} = 0)。
TSP问题是一个NP-hard问题,这意味着没有已知的多项式时间算法可以解决所有实例。因此,在实际应用中,通常使用启发式算法或近似算法来寻找可接受的解。
TSP问题在多个领域都有应用,包括:
- 物流和运输:规划车辆或飞机的最优路线以减少运输成本和时间。
- 制造业:优化机器人在生产线上的移动路径,减少生产时间和能耗。
- 电子设计自动化(EDA):在集成电路设计中,优化布线以减少电路板的长度和交叉。
- 生物信息学:在基因测序中,确定访问所有基因的最短路径以进行DNA测序。
- 计算机图形学:在渲染和动画中,优化相机路径以创建平滑的视觉效果。
2.模拟退火算法(Simulated Annealing)
模拟退火是一种受物理退火过程启发的概率搜索算法,用于在大规模搜索空间中找到近似全局最优解。算法的基本思想是从一个高温状态开始,逐渐降低温度,在每个温度下都尝试对当前解进行小的扰动,并根据Metropolis准则决定是否接受这个新解。
模拟退火算法基于Metropolis准则,该准则允许算法在搜索过程中以一定的概率接受较差的解,从而避免过早陷入局部最优。算法从一个初始解开始,并赋予它一个初始的“温度”。然后,算法在每次迭代中都会生成当前解的邻域解,并根据Metropolis准则决定是否接受这个新解。随着温度的逐渐降低,算法接受较差解的概率也逐渐减小,最终收敛到一个(近似)最优解。
算法步骤
-
初始化:选择一个初始解(S_0),设定初始温度(T_0),温度下降率(\alpha),以及最低温度(T_{min})。
-
当前解与邻域:在每次迭代中,当前解记为(S),其成本(或能量)记为(E(S))。通过某种方式生成当前解的邻域解(S'),并计算其成本(E(S'))。
-
Metropolis准则:如果(E(S') < E(S)),则无条件接受(S')作为新解。否则,以一定概率接受(S'),该概率由下式给出:

其中,(T)是当前温度。
4.温度更新:按照温度下降策略更新温度,如:
![]()
其中,a是介于0和1之间的常数。
5.终止条件:如果温度降至(T_{min})或达到预定的迭代次数,则算法终止。
3.基于模拟退火优化算法的TSP问题求解
对于TSP问题,解(S)可以表示为一个城市的排列,即(S = (s_1, s_2, ..., s_n)),其中(s_i)表示访问的第(i)个城市,且(s_{n+1} = s_1)。成本函数(E(S))可以定义为路径的总长度:
E(S)=i=1∑ndsisi+1
邻域解(S')可以通过交换、插入或倒置当前解中的城市来生成。例如,在2-opt交换中,随机选择两个不同的位置(i)和(j),然后交换这两个位置上的城市。模拟退火算法通过结合随机搜索和概率接受准则,能够在复杂的搜索空间中找到高质量的解,尤其是在存在多个局部最优解的情况下。尽管它不能保证找到全局最优解,但在实践中经常能找到非常接近全局最优的解。
4.MATLAB程序
........................................................
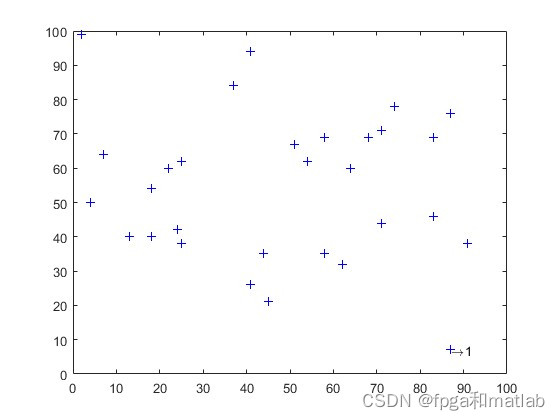
figure(1);
plot(xx,yy,'b+');text(87,7,'\rightarrow1');
xx1=xx;xx1(31)=xx(1);
yy1=yy;yy1(31)=yy(1);
figure(2);
plot(xx1,yy1);
for i=1:N
for j=1:N
if i==j
continue;
end
d(i,j)=sqrt((xx(i)-xx(j)).^2+(yy(i)-yy(j)).^2);
end
end
gen=1;
time1=datestr(now)
while gen<=10
[f,T]=trp(a,d,t0,tf);
opf(gen)=f;
path(gen,:)=T;
gen=gen+1;
end
time2=datestr(now)
disp('最小路径和')
min(opf)
disp('最优路线')
T
for i=1:N
xx2(i)=xx(T(i));
yy2(i)=yy(T(i));
end
xx2(31)=xx(1);yy2(31)=yy(1);
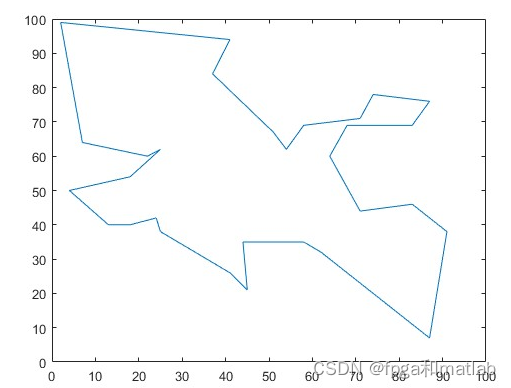
figure(3);plot(xx2,yy2);
up4013
5.仿真结果
初始的节点:
优化后的路径: