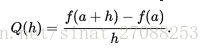翻译资料:https://en.wikipedia.org/wiki/Floating_point#Accuracy_problems
NOTE:(一)如果大家对于十进制浮点数如何转换为二进制浮点数不太清楚建议复习一下再看这篇文章,参考资料的地址
1. http://www.cnblogs.com/xkfz007/articles/2590472.html
2. http://geeklu.com/2011/03/ieee754-floating-point-arithmetic/
3. http://justjavac.iteye.com/blog/1724438
(二)加粗斜体字的翻译自己不太确定,已经在()内附上原文,不当之处请指教。
有一个事实是浮点数不能精确的代表所有实数,同时浮点操作也不能精确的表示真正的算术运算,这导致了很多奇怪情形的产生。这种问题的产生与计算机通常代表的数字是有限精度( finite precision )有关。
比如,0.1和0.01(用二进制存储时)“不可表示”的意思是:当你试图求解0.1的平方时,结果既不是0.01也不是一个接近于0.01的可表示的数。在系统为24位(单精度)表示时,0.1(十进制)是被预先给定e = −4,s = 110011001100110011001101(e是指数,s是有效数位。0.1是正数,符号位为0,
0.00011001100110011…=1.100110011001…X2^(-4),
所以其指数是-4),转换为十进制是0.100000001490116119384765625。平方之后结果为0.010000000298023226097399174250313080847263336181640625 。
但实际上最接近0.01的可表示的数是0.009999999776482582092285156250。
同样的,π或者π/2是不可表示的意味着当你尝试计算tan(π/2)时不会得到一个有限的结果,或者结果甚至会导致溢出。因为π/2不能被精确的表示,所以对于标准的浮点硬件来说尝试计算tan(π/2)是不可能的。
在C语言中的计算
/*足够的数位来确保我们可以得到正确的近似值*/
double pi = 3.1415926535897932384626433832795;
double z = tan(pi/2.0);最终得到的结果是16331239353195370.0。在类型为单精度时,运用tanf函数,结果会是−22877332.0。一样的道理,当我们尝试计算sin(π)时,也永远不会得到0的结果。在使用双精度时,结果会是(近似) 0.1225×10^-9,或者得到 −0.8742×10^−7的结果,当你采用单精度运算时。
虽然浮点数的加法和乘法是可交换的,比如a + b = b + a 以及a×b = b×a,但这并不意味着它们是可以组合计算的,比如(a + b) + c 就不一定等于a + (b + c)。
使用七个有效数位计算,例子:
a = 1234.567, b = 45.67834, c = 0.0004
而且,它们同样不一定是可分配的,比如(a + b) ×c 也许和a×c + b×c得到的结果并不一样,例子如下
1234.567 × 3.333333 = 4115.223
1.234567 × 3.333333 = 4.115223
4115.223 + 4.115223 = 4119.338
但是
1234.567 + 1.234567 = 1235.802
1235.802 × 3.333333 = 4119.340
除了某些数学定律失去意义,没有办法确切的表示诸如π 和0.1这样的数字之外,其他的一些小错误也会出现,比如:
约消:当两个接近相等的操作数相减时也许会导致完全丧失精度。当我们让两个近似相等的数字做减法时,我们把最高有效数位设置为零,留下一个误差大,不普遍的数。(When we subtract two almost equal numbers we set the most significant digits to zero, leaving ourselves with just the insignificant, and most erroneous, digits.)。比如,在确定一个函数的导数使用下列公式
从一个人的直觉出发,他会希望h是一个非常接近0的数字,但是,当我们使用浮点操作时,最小的数字并不能满足导数最佳逼近的要求。随着h变得越来越小,f (a + h) 和f(a)之间的不同也就变得越来越小。把最普遍和误差最小的数字丢弃掉,使得最大误差的数字变得十分重要(cancelling out the most significant and least erroneous digits and making the most erroneous digits more important)。结果就是,一个本身是最小数字的h可能会比一个本身是更大数字的h求导得到的误差更大。这或许是最常见但也最严重的精确度问题吧。整数转换并不直观:把63.0/9.0转换成整数最终得到7,但是把0.63/0.09转换成整数或许会得到6。这是因为转换通常是直接舍位截取而不是四舍五入。
floor(向下取整)和ceiling(向上取整)函数也许可以通过直观的计算给我们答案。有限的指数取值:结果可能上溢,无穷大或者产生下溢,得到一个比正常值要小的数字或者0。在这些情况下就会造成精度的损失。
测试除法正确性存在问题:检查除数不为零并不能够保证除法不会溢出
测试两个数字是否相等存在问题:两个在数学上相等的数列可能会产生不同的浮点数值。