学习笔记：物理渲染-间接光照

这篇文章写于开题前，离上一篇文章已经过去了快一年了，我感觉这一年收获不大，这篇文章的大部分内容也早就写在了去年的十二月份，这里只是对这篇文章内容的延伸。

在上一篇文章中，我们推导出了Cook—Torrence公式，并实现了基本的直接光照，但是对于实时渲染的场景而言，这远远不够，因为场景中的光源情况并不是单一存在的，有很多地方反射光源过来，本文章对于PRT仅仅介绍与原理，然后蜻蜓点水的将公式列出。而关于实时渲染中的球谐函数近似，IBL的方法都会列出公式以及代码。

基于图像的光照（Irradiance Based Lighting）

对于物体表面的一个点（像素而言），其受到的环境光照受到四面八方的射过来的光线的影响，无非就是一个光照的积分，代表着光线从四面八方射过来，然后乘以该光线在该点上的BRDF，以及利用cosθ得到的该光线颜色在点上的权重：

$L_{o}=\int_{\Omega}^{} L_{i}(\omega _{i}) f_{r}(\omega _{i},\omega _{o}) cos\theta d\omega _{i}$

这个公式看起来，需要对每个点计算时进行一次积分，或者说，从该点出发，往各个方向发射射线探测其颜色的，但是在实时渲染时做不到这一点，而是对于场景的环境（CubeMap）预计算得出其结果，对于漫反射（Diffuse）以及高光反射（Glossy）提前计算好结果，以在实时渲染中采样得到其正确结果。

我们将上文中的Fr，即BRDF公式，写成完整的形式：

$L_{o}=\int_{\Omega}^{}(\frac{c}{\pi}+\frac{DFG}{4(n\cdot \omega _{i})(n\cdot \omega _{o})}) L_{i}(\omega _{i}) cos\theta d\omega _{i}$

显而易见的是，可以将Diffuse与Glossy分开计算。

漫反射Diffuse的预积分贴图

将漫反射单独拎出来以后，我们可以得到漫反射的积分形式：

$L_{o}=\int_{\Omega}^{}\frac{c}{\pi} L_{i}(\omega _{i}) cos\theta d\omega _{i}$

对于物体的每一个点而言，其采样方向为以该点的法线为主轴的半球上采样的结果。需要入射的ωi转换为球面坐标。这个球面坐标是以物体的点为空间坐标中心的，我们可以看成一个寻常的半球，然后再在计算中通过空间转换转换到世界空间去（以一个球的球心为坐标轴心的世界空间）。上式Diffuse积分的立体角ωi转为球面坐标如下：

$L_{o}=\frac{c}{\pi}\int_{0}^{2\pi}\int_{0}^{\frac{\pi }{2}} L_{i }(\theta ,\phi) cos\theta sin\theta d\phi d\theta$

去除掉BRDF的部分，漫反射对于光线的积分结果（Irradiance）有：

$Irradiance=\int_{0}^{2\pi}\int_{0}^{\frac{\pi }{2}} L_{i }(\theta ,\phi) cos\theta sin\theta d\phi d\theta$

这里由于转为球面坐标的原因，每个立体角在球面上的面积微元有：dω=sinθdφ*dθ。

这里球面坐标的φ与θ的关系是由于二者在球面上的弧长比例得到的。由于θ的弧长对应的球半径是R。φ的弧长对应的球半径为sinθR。所以二者的弧长相乘的球面微元面积也应当有一个sinθ的系数。进而在积分中多出了一个sinθ的系数。

当然，从另一个角度去理解，sinθ可以当做φ随着纬度升高时的一个对应的权重，以代表纬度升高时φ的所在的微元弧度的变化。

该方程的求解无非就是两种方法，1.使用蒙特卡洛积分计算。2.利用黎曼和计算。本文在本处使用黎曼和计算积分，该方法需要在半球内采样尽可能多的离散样本然后乘以该样本对应的权重，最后求和即可。该积分可写为： $Irradiance=(2\pi-0)(\frac{\pi}{2}-0)\frac{1 }{n1*n2}\sum_{\phi=0}^{n1}\sum_{\theta=0}^{n2} L_{i }(\theta_{i} ,\phi_{j}) cos\theta_{i} sin\theta_{i} d\phi_{j} d\theta_{i}$

这个黎曼和可以直接在Shader中求出。

同时，计算球面的每个方向θi和φj时，需要将二维UV转为三维的球面坐标计算采样积分。输出的值转为一张全景图保存起来，在使用时可以转为CubeMap保存。我们可以提前用一张RenderTexture保存全景图，其图像宽高等于六面图的一面宽度width的（width*2，width），然后使用Graphic.Bilt函数保存起来：

    public void irradianceMapRenderer()
    {
        RenderTexture RT1 = new RenderTexture(targetCube.width * 2, targetCube.width, 0, RenderTextureFormat.ARGBFloat);
        RT1.wrapMode = TextureWrapMode.Repeat;
        RT1.Create();
        irradianceMaterial = new Material(irradianceShader);
        irradianceMaterial.SetTexture("_cube", targetCube);

        Graphics.Blit(null, RT1, irradianceMaterial, 1);

        xx++;
        Texture2D resultTexture = new Texture2D(targetCube.width * 2, targetCube.width, TextureFormat.RGBAFloat, true);
        RenderTexture current = RenderTexture.active;
        RenderTexture.active = RT1;
        resultTexture.ReadPixels(new Rect(0, 0, RT0.width, RT0.height), 0, 0);
        RenderTexture.active = current;
        //这里实际上进行了一次Temp操作

        byte[] TexBinary = resultTexture.EncodeToEXR(Texture2D.EXRFlags.OutputAsFloat);
        File.WriteAllBytes(Application.dataPath + "/BlogShader/BRDF/SH&Probe/NEWresultTexture" + xx + ".exr", TexBinary);

        RT1.Release();
        return;
    }

将二维UV坐标转为三维的球面坐标的原理如下，对于UV的横轴X和纵轴Y而言，其取值范围都为[0,1]，而对于球面坐标而言，其φ的取值范围为[-π,π]（一整个圆弧），θ的取值范围为[0,π]（半个圆弧），将X映射到φ，Y映射到θ，直接做一次线性映射就好了。其关系如下：

从uv.x([0,1])映射到φ([-π,π])，有 $\phi=2\pi *uv.x-\pi$
从uv.y([0,1])映射到θ([0 , π])，有 $\theta=\pi *uv.y$

同时，由于uv的Y分量的值根据DirectX与OpenGL的差异，其Y轴可能再计算时的初始坐标为左上角，所以在实际计算时，需要将Y轴的值反转，即用1.0减去即可。并且，由于使用左手坐标系的原因，用θ和φ表示球面的直角坐标系的时候，其转换有一些细节的变化，主要是Y轴变成了仰角θ所在的轴，Z轴与其替换了，所以球面坐标转换的直角坐标的Y轴分量和Z轴分量也互换了。在左手坐标系中，有坐标转换：

球面向量X分量=sin(θ)*cos(φ)
球面向量Y分量=cos(θ)
球面向量Z分量=sin(θ)*sin(φ)

则由二维的UV转换为三维球面向量的function的写法为：

        //将二维的UV全景图坐标转为三维的球面坐标
        float3 UV2normal(float2 uv)
        {
            float3 result;
            float fai=uv.x*PI*2-PI;
            float theta=(1-uv.y)*PI;
            //注意这里的是世界空间的左手坐标系
            result.x=sin(theta)*cos(fai);
            result.y=cos(theta);
            result.z=sin(theta)*sin(fai);

            result=normalize(result);
            return result;
        }

同时，在以球体为中心的世界空间中中，Y轴分量为(0,1,0)。已知一个垂直于球面的向量normal。我们将该normal视为该顶点空间中的一个基轴。那么另一个基轴tangent切线可以用normal与Y轴的叉乘得出，然后根据这两个基轴的叉乘可以得出最后一个基轴bionormal。构成基础的顶点空间的三维基轴，然后用这三个基轴构成TBN矩阵，将黎曼和的逐一计算的向量转入到世界空间去采样。（这里的原理和法线贴图转入世界空间是一模一样的，只是normal向量和tangent向量不通过obj信息得出而已）

原本我以为，需要两个pass才能实现互换，第一个pass将CubeMap转换为全景图，第二个pass在全景图上采样，后来发现没有这个必要，直接将UV转为的三维坐标转入世界空间采样CubeMap即可，完整代码有：

Shader "Hidden/irradianceShader"
{
    Properties
    {
        _MainTex("Texture",2D)="white"{}
        _cube("Reflect CubeMap",Cube)="_Skybox"{}
    }
    SubShader
    {
        CGINCLUDE
        #define PI 3.1415926535898
        #include "UnityCG.cginc"
        sampler2D _MainTex;
        samplerCUBE _cube;

        struct appdata
        {
            float4 vertex : POSITION;
            float2 uv : TEXCOORD0;
        };

        struct v2f
        {
            float2 uv : TEXCOORD0;
            float4 vertex : SV_POSITION;
        };

        v2f vert (appdata v)
        {
            v2f o;
            o.vertex = UnityObjectToClipPos(v.vertex);
            o.uv = v.uv;
            o.uv.x = 1 - o.uv.x;
            return o;
        }

        //将二维的UV全景图坐标转为三维的球面坐标
        float3 UV2normal(float2 uv)
        {
            float3 result;
            float fai=uv.x*PI*2-PI;
            float theta=(1-uv.y)*PI;
            //注意这里的是世界空间的左手坐标系
            result.x=sin(theta)*cos(fai);
            result.y=cos(theta);
            result.z=sin(theta)*sin(fai);

            result=normalize(result);
            return result;
        }

        //将三维的球面向量转为二维的UV全景图坐标
        float2 normal2UV(float3 normal)
        {
            float2 uv;
            uv.y=1.0-acos(normal.y)/PI;
            uv.x=atan2(normal.z,normal.x)/PI*0.5+0.5;
            return uv;
        }

        fixed4 fragSampler(v2f i):SV_TARGET
        {
            float3 irradiance=float3(0,0,0);
            float3 normal=UV2normal(i.uv);
            float3 tangent=float3(0,1,0);
            tangent=normalize(cross(tangent,normal));
            //切线是ObjSpaceY轴与法线叉乘得到的球面相切的方向
            float3 bionormal=normalize(cross(normal,tangent));
            //获得三个轴的朝向

            float sampleDelta=0.025;
            float sampleCount1=0.0;
            float sampleCount2=0.0;

            for(float phi=0.0;phi<2.0*PI;phi+=sampleDelta)
            {
                for(float theta=0.0;theta<0.5*PI;theta+=sampleDelta)
                {
                    float3 tangentSample=float3(sin(theta)*cos(phi),sin(theta)*sin(phi),cos(theta));
                    //构建当前角度的一个标准的球面坐标（r=1）
                    float3 sampleVec=tangentSample.x*tangent+tangentSample.y*bionormal+tangentSample.z*normal;
                    //从切线空间空间转换到世界空间的矩阵，列向量分别是(T,B,N)
                    irradiance+=texCUBE(_cube,sampleVec).rgb*cos(theta)*sin(theta);
                    sampleCount1++;
                }
            }
            float wight=PI/(sampleCount1);
            return float4(irradiance*wight,0);
        }
        ENDCG
        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment fragSampler
            ENDCG
        }
    }
}

从这个方法可以得出一个CubeMap的IrradianceMap的全景图形式，可以通过一些逻辑（或者是插件）生成对应的CubeMap，这里就不赘述了。初始图像的全景图和结果的全景图如下：

输入的CubeMap和输出的CubeMap结果分别如下：

使用以上的方法渲染IrradianceMap虽然逻辑简单，但是对于一个复杂光照的场景而言，在计算该场景中物体光照时，不仅需要存储场景光照的CubeMap，还需要多附带一个CubeMap存储Irradiance信息，对于一些轻量平台而言并不是一个好方法，所以PRT引入了基函数来表示低频的Irradiance光照情况。

利用球面谐波基函数预积分Diffuse

首先我们可以知道，由于场景中的光照环境比较复杂，引入了环境的球体即CubeMap来描述场景中环境的整体效果。从上文中的公式可以看出，如果要计算一个点受到环境光照的具体情况，需要预计算好该环境光照的积分然后实时采样这个积分结果，但是，如果当前场景是动态的，或者值发生了偏移，则需要预积分多张CubeMap才能满足需求。尤其是CubeMap发生旋转的情况，如果对要使用的环境光照每个角度都要Render一次，实在是一个很费的方法。所以PRT中，利用了基函数来代替原本的光照积分，低频的环境光照信息，物体的每个采样点对于仅需要保存一定数量的基函数即可，并且也支持随时旋转的环境光照信息。这里的基函数并不仅限于常见的球谐基函数，还有例如小波基函数或者球面高斯基函数等也在图形学中有应用。

在理解并实现球谐（球面谐波 Sphere Harmonics）函数的时候，并不需要摆出太多的数学公式去解构它，过多的引入一些数学概念和公式并不有益于我们理解球谐近似的实现。我们只需要知道，正如傅里叶变换那样，高频、复杂的函数可以用数个低频的，简单的基函数（经典三角函数sin和cos）的和近似表达，球谐基函数也正是从这一原理出发，它仅仅是一组定义在球面的基函数罢了，我们使用若干个球谐基函数与原函数得出这些基函数对应的权重系数，然后在实时计算时仅仅需要这些基函数乘以权重的累加，便可获得原函数的近似。

从球面谐波基函数这个名字就可以看出，它定义在球面上的一组基函数，那么它的输入值即为球面坐标θ和φ（或者是球面坐标转的三维坐标）。它的写法是 $Y_{m}^{l}$ ，其中 $l$ 代表该基函数所在的层数（频率系数），从0阶开始计数。 $m$ 代表该基函数是所在的阶 $l$ 的第几个系数，与 $l$ 存在 $-l \leq m \leq l$ 的关系，并且，每一层存在 $2l+1$ 个基函数，同时，对于n个层数而言，存在的球谐基函数的数量为 $n^{2}$ 个。用公式可以将球谐基函数 $Y_{m}^{l}$ 写为：

$Y_{l}^{m}(\theta,\phi)=K_{l}^{m}e^{im\phi}P_{l}^{|m|}(cos\theta)$

其中， $P_{l}^{m}$ 为关联勒让德多项式，而 $K_{l}^{m}$ 为归一化因子，它的值与当前基函数的 $l$ 和 $m$ 有关:

$K_{l}^{m}=\sqrt{\frac{(2l+1))}{4\pi}*\frac{(l-|m|)!}{(l+|m|)!}}$

通过简单的变换，球谐基函数可以根据 $m$ 划分为：

$Y_{l}^{m}(\theta,\phi)=\left\{\begin{matrix} \sqrt{2}K_{l}^{m}cos(m\phi)P_{l}^{m}(cos\theta) \;\; \; \; \; \; \; \; \; \; m>0 \\ \sqrt{2}K_{l}^{m}cos(-m\phi)P_{l}^{-m}(cos\theta) \;\; \; \; \; \; m<0 \\ K_{l}^{0}P_{l}^{0}(cos\theta) \;\; \; \; \; \; \; \; \; \; \; \; \ \; \; \; \; \ \; \; \; \; \ \; \; \; \; \; \; \; \;m=0 \end{matrix}\right.$

如何推导某一个 $l$ 和 $m$ 对应的球谐基函数并不是我们使用它的重点，由于它们内部计算方法已经定好，其值仅根据输入的θ和φ决定，我们可以从这里查询每一阶的球谐基函数的逻辑（维基百科中坐标系默认为右手坐标系），输入自己需要的值即可计算出任意基函数的结果。网络上，描述球谐基函数的图像都是如下的一张图：

在图像中，绿色为正值，红色为负值，并且离球中心越远的地方绝对值越大，我们可以理解为，球谐基函数往哪个方向突出，就是说明，该在球面这个方向有值，突出的程度代表值的大小。并且显而易见的是，随着阶数的升高，球谐的分布越来越复杂，方向也越来越多样。

例如，对于零阶的球谐基函数而言，即为一个纯颜色的球体（0层右上角那个纯色的绿圆球），这代表一阶在球面任何方向的值都是一致的，从实际的球谐值看（一阶的球谐值为 $\frac{1}{2}*\sqrt{\frac{1}{\pi}}$ ），零阶的球谐基函数的值也确实为定值。而对于一阶二阶以至于多阶而言，我们可以知道，每一阶内部多个基函数的值不同，朝向也不同。

循着上文中获得的球谐基函数的值，我们可以简单的写出前四层、16个球谐函数：

    List<double> BasisY(Vector3 pos)
    {
        List<double> Y = new List<double>(degree);
        Vector3 normal = Vector3.Normalize(pos);
    	float x = normal.x;
    	float y = normal.y;
    	float z = normal.z;

    	if (degree >= 1)
    	{
    		Y.Add(1.0f / 2.0f * Mathf.Sqrt(1.0f / Mathf.PI));
    	}
    	if (degree >= 4)
    	{
    		Y.Add(Mathf.Sqrt(3.0f / (4.0f * Mathf.PI)) * z);
    		Y.Add(Mathf.Sqrt(3.0f / (4.0f * Mathf.PI)) * y);
    		Y.Add(Mathf.Sqrt(3.0f / (4.0f * Mathf.PI)) * x);
    	}
    	if (degree >= 9)
    	{
    		Y.Add(1.0f / 2.0f * Mathf.Sqrt(15.0f / Mathf.PI) * x * z);
    		Y.Add(1.0f / 2.0f * Mathf.Sqrt(15.0f / Mathf.PI) * z * y);
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(5.0f / Mathf.PI) * (-x * x - z * z + 2 * y*y));
    		Y.Add(1.0f / 2.0f * Mathf.Sqrt(15.0f / Mathf.PI) * y * x);
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(15.0f / Mathf.PI) * (x * x - z * z));
    	}
    	if (degree >= 16)
    	{
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(35.0f / (2.0f * Mathf.PI)) * (3 * x * x - z * z) * z);
    		Y.Add(1.0f / 2.0f * Mathf.Sqrt(105.0f / Mathf.PI) * x * z * y);
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(21.0f / (2.0f * Mathf.PI)) * z * (4 * y * y - x * x - z * z));
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(7.0f / Mathf.PI)*y*(2 * y*y - 3 * x*x - 3 * z * z));
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(21.0f / (2.0f * Mathf.PI)) * x * (4 * y * y - x * x - z * z));
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(105.0f / Mathf.PI) * (x * x - z * z) * y);
    		Y.Add(1.0f / 4.0f * Mathf.Sqrt(35.0f / (2 * Mathf.PI)) * (x * x - 3 * z * z) * x);
    	}
        return Y;
    }

并且，球谐基函数存在两个非常重要的性质，我们在下文中就会应用它们：

旋转不变性：球谐基函数定义在球面，所以任意球谐基的旋转可以用同阶基函数的线性表示。并且，对于光照信息发生旋转的场景而言，旋转光照等于旋转球谐基函数。这使得场景中的光照在发生偏移时光照结果不会发生撕裂，混叠等异常现象，这也是实时渲染中引入球谐基函数的重要原因之一。例如一个向量s，它的球谐函数表示为f(s)，将输入的向量s旋转Q(vector)的角度与旋转球谐函数的作用是一样的有： $f(Q(s))=Q(f(s))$
正交完备性：球谐函数是互相正交的，两个不同的基函数乘积的积分都为0，仅当两个基函数相同时函数乘积的积分为1。（这里在闫令琪老师的课里有一个比喻，我们可以将每一层内部的基函数理解为类似于三维空间的基轴XYZ，这三个基轴仅投影到自身时才有值，而投影到其他轴上的时候由于互相垂直的原因，投影结果一定是0。）类似地认为是写成公式如下：

$\int_{\Omega}Y_{l}^{m}(\omega )*Y_{k}^{n}(\omega )=\left\{\begin{matrix} 1 \, \, \, \, \, \, \, \, \, \, \, \, \, m==n\, \, and \, \, k==l\\ 0 \, \, \, \, \, \, \, \, \, \, \, \, \,\, \, \, \, \, \, \, \, \ m!=n\, \, or \, \, k!=l \end{matrix}\right.$

同时，球谐基函数也可以写成一维的形式，仅仅是做一下写法上的替换罢了。有 $Y_{l}^{m}(\theta , \phi )=Y_{i}(\theta , \phi )$ ， $l$ 、 $m$ 和 $i$ 的关系是： $i=(l+1)*l+m$ 。在下文中，我们使用 $Y_{i}$ 的形式来更加简便地表示基函数。对于任意的一个函数F(x)（这个函数也是我们需要用基函数近似的函数，至于输入可以是θ和φ，也可以是它们转为直角坐标系的值x），可以用N个基函数Bi乘以各自对应的权重系数Ci得出：

$f(\theta,\phi)=\sum_{l=0}^{\infty } \sum _{m=-l}^{l }c_{l}^{m}*Y_{l}^{m}(\theta,\phi) =\sum_{i=1}^{n^{2} } c_{i}*Y_{i}(\theta,\phi)$

只要N的层数越多，越能接近F(x)的本来性质。基函数只需要按照输出的值利用对应的层数上定死的逻辑计算则可，反而计算每个基函数各自对应的权重才是计算量的大头，而对于球谐基函数的权重系数Ci而言，它与基函数和需要还原的任意函数F(x)的关系是：

$c_{i}=\int_{\Omega }^{ } f(x)*Y_{i}(x)$

将任意函数f(x)生成若干个基函数与权重系数线性组合过程，称为投影(Projection)。而相对应的是，将基函数乘以对应系数近似原函数的过程，这个的过程称为重建(Reconstruction)。从这个关系可以得知，对于第i个球谐基函数Bi对应的权重系数Ci而言，其值等于原函数乘以其对应的基函数在球面上的积分结果。这也是我们在利用球谐函数计算DiffuseIrradianceMap时的重点之一。

基于球谐函数的预计算光线传输（Precomputed Radiance Transfer.PRT）

        场景中，假设物体上的某一点不存在自发光，并且受到的环境光照无限远，受到的光照的值有入射光线、BRDF、该点可见性以及平衡项cosθ的积分：

                                                $L_{o}=\int_{\Omega}^{} L_{i}(\omega _{i}) V(\omega _{i})f_{r}(\omega _{i},\omega _{o}) cos\theta d\omega _{i}$

其中 $V(\omega _{i})$ 表示当前点在ωi方向上的可见性，对于物体的凹面需要这个函数来影响该点受到光线的情况，而对于物体的凸面则可以隐去该项。在PRT的思想里，将Lo的球面积分分为两个部分，一个是Li(ωi)，将其称之为Lighting，即光照项。另一个即为V，fr，cosθ的乘积，统称为lightTransport，即为光照传输项。首先处理Lighting项，将其利用球谐基函数表示，这里的Li即为上文中已知的任意函数f(x)，那么显然可以表示方向i的光照函数有：

                                                          $L_{i}\approx \sum _{i}l_{i}*B_{i}$

如果假设场景中仅有光照条件发生变化（即光源或者环境光照发生变化），场景本身的性质（例如物体材质以及位置，摄像机的坐标以及方向）不发生变化，显然LightTransPort项可以提前预计算出来。由于对于一个点的漫反射而言，其辐射度向球面四周均匀地扩散，不受到视角ViewDir的影响，所以可以将Diffuse的BRDF作为常数。同时，Lighting项的且基函数权重系数 $l_{i}$ 也是常数，我们可以把这两个值从积分中拉出来，原式变为：

                                          $L_{o}=fr_{diffuse}\sum_{i}l_{i} \int_{\Omega}^{} B_i(\omega _{i}) V(\omega _{i}) cos\theta d\omega _{i}$

这时我们可以看到，积分内部仅仅存在光照基函数Bi，可见性函数V，和一个cosθ，我们将V和cosθ视为剩下的LightTransPort视为一个函数，称其为F(x)，同样的，它可以利用基函数表达：

                                                 $f(x)=V(\omega_{i})cos\theta_{i}=\sum _{j}c_{j}*B_{j}(x)$

将这个基函数与系数的组合也代入到Lo的积分中，同样的，权重系数也可以提出积分，有如下表达形式：

                                                 $L_{o}=\sum_{i=0}l_{i}\sum_{j=0}c_{j}\int_{\Omega}B_{i}(\omega)B_{j}(\omega)d\omega$

        此时的积分内部恰好符合球谐基函数的正交完备性的定义，两个球谐基函数相乘在球面的积分，如果两个基函数并不是同层同阶即为0，同层同阶即为1，所以球谐基函数Bi和Bj的积分仅有0和1两种情况，所以出射辐射度Lo等于Lighting的基函数系数 $l_{i}$ 和LightTransport的基函数系数 $c_{i}$ 的乘积的累加：

   $L_{o_{diffuse}}\approx fr_{diffuse}*\sum_{i}l_{i}*c_{i}$

对于物体上的每个像素点而言，仅仅需要保存系数 $c_{i}$ 的Vector（PRT中称之为transfer vector），在实时渲染中与Lighting 的系数 $l_{i}$ 相乘累加然后乘以diffuse的BRDF系数即可得到Diffuse的环境光照结果。当然，为了得出这两个权重系数，还是要各自算一次积分的，即：

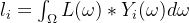
                  $l_{i}=\int_{\Omega}L(\omega)*Y_{i}(\omega)d\omega$    $c_{i}=\int_{\Omega}V(\omega)cos\theta*Y_{i}(\omega)d\omega$

计算Lighting积分光线直接从CubeMap采样即可，而计算LightTransPort的积分中的θ角为表面法线n与球面向量角ω的夹角，所以计算LightTransPort项的权重需要有两个循环，第一次遍历球面的法线normal，每个法线方向遍历一次球面立体角方向ω（即CubeMap像素所在的球面方向）。

        而对于Glossy而言，由于高光BRDF不仅与入射角ωi有关，还与出射角ωo有关，所以并不能简单的通过保存一组系数来预计算，每个点出射辐射度有：

                                                     $L_{o_{glossy}}\approx \sum_{i}l_{i}*T_{i}(o)$

其中Ti(o)为该点的LightTransPort，由于该值与入射出射两个系数相关，是一个二维的数据，需要使用一个矩阵Mp来表示它，并且并不能像Diffuse那样将BRDF提出到积分外部，例如Mp的第i行第j列的数据表示某一输入输出向量对应的球谐基函数的系数对结果的线性影响。所以，场景中的每个点都需要保存这样一个系数矩阵，然后在实时计算中使用该矩阵乘以 Lighting 的系数 $l_{i}$ ，获得最终正确的结果，利用球谐来近似Glossy现象的缺点是：每个点都要保存一个矩阵很消耗资源，并且，由于球谐函数的性质更合适于描述低频函数，利用球谐基函数生成高频图像需要阶数达到一定的量级才能得到比较优秀的近似结果，这进一步加大了矩阵的数量级，所以球谐基函数在近似Glossy效果上并不不是一个很好的方法。

以上Sloan在著名文章《Precomputed Radiance Transfer for Real-Time Rendering in Dynamic,Low-Frequency Lighting Enviroment》（简称PRT）中利用球谐函数预计算环境光照的Diffuse和Glossy的方法。在引擎实时渲染中，我们并不能像PRT的那样，仅仅计算两个系数的乘积即可。主要是LightTransPort需要提前获得物体表面法线，并且对于凹面还需要计算可见性函数，这并不适用于我们在引擎中使用球谐函数的情况。在实时渲染引擎中，仅仅完成了PRT中的第一步，即将利用基函数将图像在低频中重建。计算原本需要利用卷积算出来的Diffuse预积分的效果。即这个关系：

$L_{i}\approx \sum _{i}l_{i}*B_{i}$

对于CubeMap而言，其球面上的颜色可以抽象为与球面法线Normal相关的函数，那么基函数的输入即为球体法线normal(x,y,z)，而环境光照的原函数Li(x)即为CubeMap的表面法线normal对应的表面颜色。总的来说，即将CubeMap每个像素都视为一组光线入射，将每条入射光线都分解为一组球谐基函数中。

在这一点上同时需要知道的是，图像大部分的能量集中在球谐函数的前三阶（0,1,2）对应的9个球谐基函数上，对应到现实物体中，这个现象的体现就是空间中物体低频信息往往大于高频信息，所以较低阶的基函数就能恢复图像原本的性质。而在实际的计算中，重点则放在了如何计算这些球谐基函数的系数上，我们回顾上文说的球谐函数的概念可知，投影获得系数序列的过程需要在球面对每个原函数F(x)和对应这个球面向量的基函数积分，即：

$c_{i}=\int_{\Omega}L(\omega)Yi(\omega)d\omega=\sum_{j}L_{j}Y_{i}(j)$

且由于Li来自于CubeMap中，为受到分辨率制约的离散值，所以CubeMap采样得出的每个像素的颜色值都需要乘以该像素对应的立体角的“微元”面积。将CubeMap对应像素计算其对应立体角微元的方法的逻辑推导可以看这篇博客。所以上文的累加可以详细写为：

$c_{i}=\sum_{j}L_{j}Y_{i}(j)=\sum_{\omega}^{\Omega}Y_{i}(\omega)*texCube(\omega)*d\omega$

即对于CubeMap而言，遍历每个像素并获得其对应立体角，采样该立体角上的CubeMap颜色并乘以其立体角微元，同时计算出其球谐基函数，相乘并累加得到基函数的系数，在本文中，我们选择在C#脚本中完成全部操作（主要是在Shader中操作CubeMap有一丢丢麻烦），对于CubeMap，输入其六个面的图像，计算Ci，然后将Ci乘以对应的球谐基函数的结果放入六张新创建的图像里，保存到CubeMap中。

并且，为了计算基函数，需要将CubeMap的六面体的表面UV转为球面向量，我们假设六面体组成的正方形边长为2，直角坐标系轴（坐标轴为左手坐标系）轴心位于正方形中心。当计算某一面Face上的某一像素uv时，面所在的主轴固定，剩余两个边长的取值范围在[-1,1]之间（所以UV首先要映射到[0,1]之间，然后映射到[-1,1]之间）。例如，+X面对应的所有球面向量的X轴分量都是1，-Z面对应的所有球面向量的Z轴分量都是-1。同时需要注意的是，每个面UV都设定为左下角为原点（uv=(0,0)），自然右上角为uv结束的点（uv=(0,0)）。（需要注意的是，这里的左下角和右上角是从坐标轴轴心往这些方向去看的）。借用一些大佬博客的图片：

照着这个逻辑去匹配遍历的CubeMap六个面的像素，代码有：

UV2XYZ(int index,Vector2 uv)
    {
        float u = uv.x * (float)2 - 1.0f;
        float v = uv.y * (float)2 - 1.0f;
        switch(index)
        {
            case 0: return new Vector3( 1.0f,  v, -u ); // +x
	        case 1: return new Vector3( -1.0f,  v,  u); // -x
	        case 2: return new Vector3( u,  1.0f, -v ); // +y
	        case 3: return new Vector3( u, -1.0f,  v );	// -y
	        case 4: return new Vector3( u,  v,  1.0f ); // +z
	        case 5: return new Vector3( -u,  v, -1.0f);	// -z
        }
        return Vector3.zero;
    }

其中index为输入的面的序号，uv则是该面上图像的UV序号，取值范围为[0,width]和[0,height]。根据这样的方法我们可以得出六面体每个面的二维UV转为的三维坐标。然后我们就可以顺利的遍历六面体的所有坐标得出总的基函数系数了：

    Vector3[] evaluateCoefs(int width,int height)
    {
        Vector3[] coefs_m = new Vector3[degree];
        for (int t = 0; t < degree;t++)
        {
            coefs_m[t] = Vector3d.zero;
        }

        for (int k = 0; k < 6; k++)
        {
            for (int j = 0; j < height; j++)
            {
                for (int i = 0; i < width; i++)
                {
                    float px = (float)i + 0.5f;
                    float py = (float)j + 0.5f;
                    float u = 2.0f * (px / (float)width) - 1.0f;
                    float v = 2.0f * (py / (float)height) - 1.0f;
                    //将值的范围压缩到(-1,1)
                    float dx = 1.0f / (float)width;
                    float dy = 1.0f / (float)height;
                    //像素的一个阶

                    float x0 = u - dx;
                    float y0 = v - dx;
                    float x1 = u + dx;
                    float y1 = v + dx;
                    //设置uv周围以width的边界
                    //关于这里的逻辑的解释：https://www.rorydriscoll.com/2012/01/15/cubemap-texel-solid-angle/

                    float da = surfaceArea(x0, y0) - surfaceArea(x0, y1) - surfaceArea(x1, y0) + surfaceArea(x1, y1);

                    v = 1.0f - (float)j / ((float)height - 1.0f);
                    u = (float)i / ((float)width - 1.0f);

                    Vector3 pos = CubeUV2XYZ(k, new Vector2(u, v));

                    Color c = targetTexs[k].GetPixel(i, height-j);

                    Vector3 targetColor = new Vector3(c.r*da, c.g*da, c.b*da);
                    List<double> Y = BasisY(pos);

                    for (int t = 0; t < degree; t++)
                    {
                        coefs_m[t] += Y[t] * targetColor;
                    }
                }
            }
        }
        return coefs_m;
    }

由于CubeMap的特性，在粘贴图像的时候我发现CubeMap中图像的V轴为反，所以需要在GetPixel函数上取反方向height-j。对于整个CubeMap而言，球谐基函数系数的数组仅为9，这是由于其在积分上定义的性质而来的。得到这个系数数组以后，将每个像素所在的球面向量对应的基函数按序号乘以该系数数组，就可以得到原本图像的低频形态：


    Vector3d Render(Vector3 pos,Vector3[] coefs)
    {
        List<double> Y = BasisY(pos);
        Vector3 pixelCol = Vector3.zero;
        for (int i = 0; i < degree; i++)
        {
            pixelCol += Y[i] * coefs[i];
        }
        return pixelCol;
    }

    Texture2D[] RenderCubeMap(int width, int height,Texture2D[] imgs,Vector3[] coefs)
    {
        for (int k = 0; k < imgs.Length;k++)
        {
            for (int i = 0; i < width; i++)
            {
                for (int j = 0; j < height; j++)
                {
                    float v = 1.0f-(float)j / (height - 1.0f);
                    float u = (float)i / (width - 1.0f);
                    Vector3 pos = CubeUV2XYZ(k, new Vector2(u, v));
                    
                    Vector3 col = Render(pos, coefs);
                    imgs[k].SetPixel(i, j, new Color(col.x, col.y, col.z, 1.0f));
                }
            }
        }
        return imgs;
    }

然后将六个面依次进行计算，每次计算时乘以系数与对应的基函数，使用一个总的函数包装这些方法，然后将输入的六面图像的值保存到一张CubeMap当中去：


    public void spit2Cube()
    {
        degree = 9;
        int width = targetTexs[0].width;
        int height = targetTexs[0].height;
        Texture2D[] imgs = new Texture2D[6];
        for (int i = 0; i < 6;i++)
        {
            imgs[i] = new Texture2D(width, height, TextureFormat.RGBAFloat, true);
        }

        Vector3d[] coefs = evaluateCoefs(width, height);
        //计算九个球谐基函数的系数
        imgs = RenderCubeMap(width, height, imgs, coefs);
        //将系数乘以对应的基函数的方法

        newCube = new Cubemap(512, TextureFormat.ARGB32, true);
        CubemapFace face = CubemapFace.PositiveX;

        for (int i = 0; i < 6;i++)
        {
            newCube.SetPixels(imgs[i].GetPixels(), face);
            face += 1;
            newCube.Apply();
        }
        string fileName = ".../BRDF/SH&Probe/HaromoneySpherical" + x + ".cubemap";
        AssetDatabase.CreateAsset(newCube, fileName);
        x++;
    }

这里只是简单的将方法整合到了一个函数当中去，然后算出的结果保存为一张CubeMap。其中三阶球谐基函数（即9个基函数）的计算结果如下，如图，左边为Unity官方的StandardMaterial中Smooth=0.33的结果，右图为我们使用三阶球谐基函数的计算结果：

我们使用2阶球谐基函数，与上文中使用预积分方法得出的IrradianceMap（中）和StandardMaterial中Smooth=0.13的CubeMap进行比较，可以看到，球谐函数在还原IrradianceMap时细节比预积分方法要丰富一些：

那么。Unity中是如何运用球谐函数的呢，在UnityShader的UnityShaderVariables.cginc文件里，对球谐基函数以及它们的系数有如下定义：

    // SH lighting environment
    half4 unity_SHAr;
    half4 unity_SHAg;
    half4 unity_SHAb;
    half4 unity_SHBr;
    half4 unity_SHBg;
    half4 unity_SHBb;
    half4 unity_SHC;

这里保存的值可以理解为当前场景中的9个球谐基函数和对应的系数相乘的结果（并未代入当前法线方向）。这里定义了七个float4，共28个数，对于二阶（三层）的球谐函数存在9个的基函数，每个基函数对应的系数根据（r,g,b）的原则，乘起来正好是27个。例如以unity_SHAr为例，它的四个分量分别为：

$unitySHAr.x=(c_{1}^{-1}.r)Y_{1}^{-1}$
$unitySHAr.y=(c_{1}^{0}.g)Y_{1}^{0}$
$unitySHAr.z=(c_{1}^{1}.b)Y_{1}^{1}$
$unitySHAr.w=c_{0}^{0}.r$

由于对于球谐基函数来说，对于代入的值球面向量可以在计算时才代入，这里并没有代入具体的哪个球面向量，仅仅是球谐基函数前面的式子和系数的乘积。在Lighting.hlsl文件中的定义中，有如下对三层的球谐基函数的采样的方法：

这个函数定义在Lighting.hlsl中
// Samples SH L0, L1 and L2 terms
half3 SampleSH(half3 normalWS)
{
    // LPPV is not supported in Ligthweight Pipeline
    real4 SHCoefficients[7];
    SHCoefficients[0] = unity_SHAr;
    SHCoefficients[1] = unity_SHAg;
    SHCoefficients[2] = unity_SHAb;
    SHCoefficients[3] = unity_SHBr;
    SHCoefficients[4] = unity_SHBg;
    SHCoefficients[5] = unity_SHBb;
    SHCoefficients[6] = unity_SHC;

    return max(half3(0, 0, 0), SampleSH9(SHCoefficients, normalWS));
}

以下的函数定义在EntityLighting.hlsl中
float3 SampleSH9(float4 SHCoefficients[7], float3 N)
{
    float4 shAr = SHCoefficients[0];
    float4 shAg = SHCoefficients[1];
    float4 shAb = SHCoefficients[2];
    float4 shBr = SHCoefficients[3];
    float4 shBg = SHCoefficients[4];
    float4 shBb = SHCoefficients[5];
    float4 shCr = SHCoefficients[6];

    // Linear + constant polynomial terms
    float3 res = SHEvalLinearL0L1(N, shAr, shAg, shAb);

    // Quadratic polynomials
    res += SHEvalLinearL2(N, shBr, shBg, shBb, shCr);

#ifdef UNITY_COLORSPACE_GAMMA
    res = LinearToSRGB(res);
#endif

    return res;
}

// Ref: "Efficient Evaluation of Irradiance Environment Maps" from ShaderX 2
real3 SHEvalLinearL0L1(real3 N, real4 shAr, real4 shAg, real4 shAb)
{
    real4 vA = real4(N, 1.0);

    real3 x1;
    // Linear (L1) + constant (L0) polynomial terms
    x1.r = dot(shAr, vA);
    x1.g = dot(shAg, vA);
    x1.b = dot(shAb, vA);

    return x1;
}

real3 SHEvalLinearL2(real3 N, real4 shBr, real4 shBg, real4 shBb, real4 shC)
{
    real3 x2;
    // 4 of the quadratic (L2) polynomials
    real4 vB = N.xyzz * N.yzzx;
    x2.r = dot(shBr, vB);
    x2.g = dot(shBg, vB);
    x2.b = dot(shBb, vB);

    // Final (5th) quadratic (L2) polynomial
    real vC = N.x * N.x - N.y * N.y;
    real3 x3 = shC.rgb * vC;

    return x2 + x3;
}

SampleSH非常简单，获得七个存储球谐基函数的数值，然后将它们和输入的法线N一起传入SampleSH9中，SampleSH9首先拿到这些值，然后将前两阶和第三阶分开计算（因为第三阶设计一些N的分量互相的四则运算）。算好后根据是否需要进行Gamma矫正来进行色域上的操作。在我们实际在Shader中获得球谐函数近似的IrradianceMap图像时，使用UnityCG.cginc中的ShadeSH9函数，其实参是当前物体的世界空间法线向量。其内部逻辑如下：

half3 ShadeSH9 (half4 normal)
{
    // Linear + constant polynomial terms
    half3 res = SHEvalLinearL0L1 (normal);

    // Quadratic polynomials
    res += SHEvalLinearL2 (normal);

#   ifdef UNITY_COLORSPACE_GAMMA
        res = LinearToGammaSpace (res);
#   endif

    return res;
}

参考文献：

球谐函数部分：

https://zhuanlan.zhihu.com/p/452190320

https://blog.csdn.net/qq_33999892/article/details/83862583

球谐光照与PRT学习笔记（三）：球谐函数 - 知乎

https://en.wikipedia.org/wiki/Associated_Legendre_polynomials

【论文复现】Spherical Harmonic Lighting:The Gritty Details - 知乎

[Unity]IBL-使用预计算辐射照度图的漫反射 - 知乎

实时渲染｜Precomputation-Based Rendering ：PRT部分 - 知乎

GAMES202-高质量实时渲染_哔哩哔哩_bilibili

球谐光照——球谐函数 - 知乎

http://www.ppsloan.org/publications/StupidSH36.pdf