前言
老师讲这个方向的知识讲了几节课了,然而我都在划水中,所以想着要不再补补,我可能要寄了,所以有此篇
正文

首先咱们看一看大纲,这大纲都讲了些啥呢
- Modeling for Imaging Pipeline(成像管道建模):对摄像头的成像过程进行建模,包括光学畸变、相机内参和外参等因素。
- General Framework for the Camera Calibration Algorithm(摄像头标定算法的通用框架):摄像头标定算法的一般框架,包括校准板图像采集、特征提取、相机参数估计和误差优化等步骤。
- Initial Rough Estimation of Calibration Parameters(初始标定参数的粗略估计):对摄像头的内部和外部参数进行初步估计,以提供标定算法的初始值。
- Nonlinear Least-squares(非线性最小二乘法):一种常用的优化方法,用于通过最小化观测数据与模型之间的残差来估计摄像头的标定参数。
- Bird's-eye-view Generation(鸟瞰图生成):利用摄像头标定参数将摄像头图像转换为鸟瞰视图,以提供更全局的场景观察和测量。
- 摄像头标定(他喵的这是第一个我忘记加上去了)
总之先从摄像头标定开始说起吧
摄像头标定
摄像头标定是通过确定摄像头的内部和外部参数,使其能够准确测量和重建三维世界中的物体。摄像头标定对于计算机视觉和计算机图形学中的许多应用都是至关重要的,如目标检测、姿态估计、虚拟现实等。
摄像头标定的过程包括以下步骤:
1. 数据采集:在进行摄像头标定之前,需要采集一组已知的参考图像或视频。通常使用标定板或标定物体,其具有已知的几何形状和尺寸。
2. 特征提取:从采集到的图像中提取特征点,用于后续的摄像头参数估计。常用的特征点包括角点、线条或纹理等。
3. 内部参数估计:内部参数是指摄像头的光学特性和成像参数,如焦距、主点位置、像素尺寸等。通过对标定板图像中的特征点进行分析和计算,可以估计出这些内部参数。
4. 外部参数估计:外部参数是指摄像头相对于世界坐标系的位置和姿态,也称为摄像头的位姿。通过将标定板置于已知的位置和姿态下,结合摄像头图像中的特征点信息,可以估计出摄像头的外部参数。
5. 畸变校正:光学畸变是摄像头成像过程中的一种失真,会导致图像中的直线变形或形状扭曲。在摄像头标定中,通常也会对光学畸变进行建模和校正,以提高测量的准确性。
6. 误差优化:在进行摄像头标定时,通常会存在一些测量误差。为了提高标定的精度,可以采用非线性最小二乘法等优化方法,通过最小化观测数据与模型之间的残差来优化摄像头参数的估计结果。
完成上述步骤后,就可以得到摄像头的内部和外部参数,从而使摄像头能够准确测量和重建场景中的物体。这些参数可以用于计算机视觉和计算机图形学中的各种应用,例如目标检测、相机跟踪、三维重建等。
需要注意的是,摄像头标定的精度和准确性对于应用的成功与否至关重要。因此,在进行摄像头标定时,需要仔细选择标定物体、合理安排标定图像的采集,并进行适当的误差分析和校正,以确保标定结果的可靠性。
成像管道建模

这是PPT上的过程,展开来讲,就是为了对图像形成过程进行建模,需要使用四个坐标系来描述不同阶段的坐标转换和变换。这些坐标系包括:
1. 世界坐标系(World coordinate system):世界坐标系是三维空间中的坐标系,用于描述场景中物体的位置和姿态。在世界坐标系中,物体的位置和方向是相对于一个参考点或参考物体确定的。
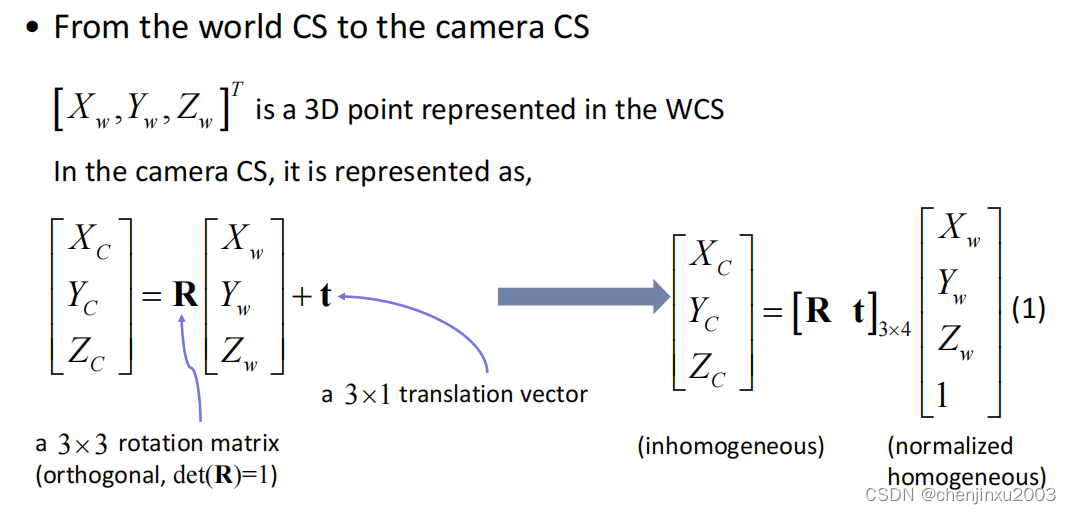
2. 摄像头坐标系(Camera coordinate system):摄像头坐标系是相机内部的坐标系,用于描述相机的位置和朝向。摄像头坐标系的原点通常位于相机的光心(光学中心),坐标轴与相机的光学轴对齐。
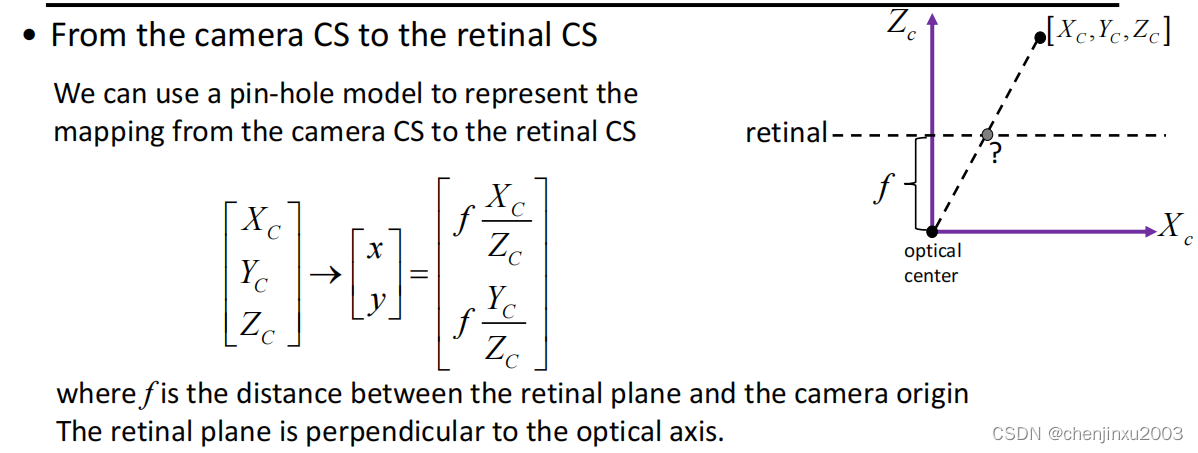
3. 视网膜坐标系(Retinal coordinate system):视网膜坐标系是相机传感器上的坐标系,用于描述相机传感器上的像素位置。视网膜坐标系的原点通常位于传感器的中心,坐标轴与传感器平面对齐。

4. 归一化视网膜坐标系(Normalized retinal coordinate system):归一化视网膜坐标系是视网膜坐标系的变换形式,通过将像素坐标归一化到范围 [0, 1] 内,方便进行图像处理和算法计算。
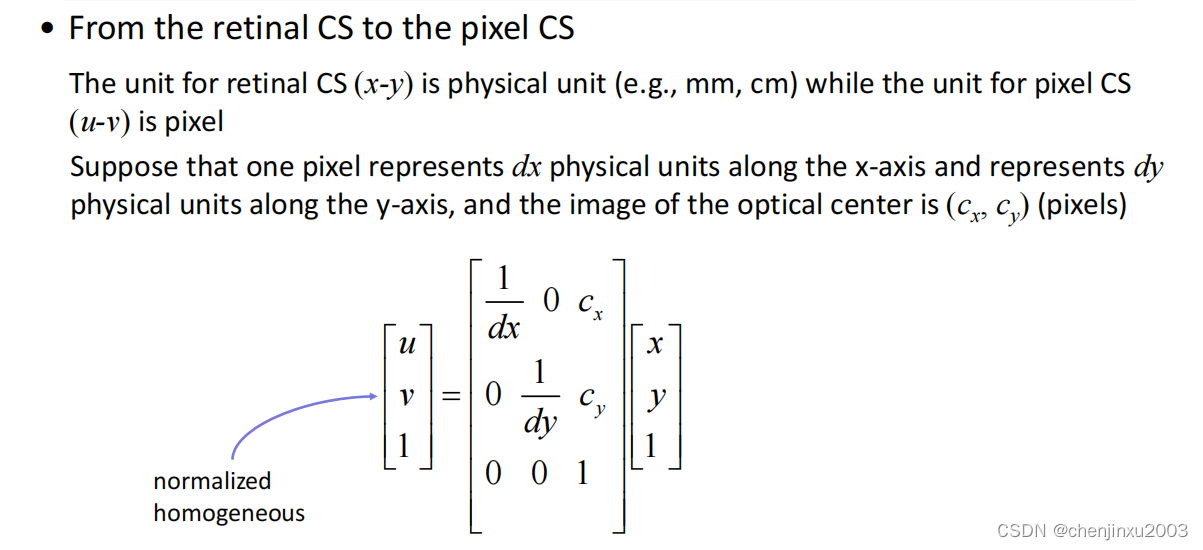
5. 像素坐标系(Pixel coordinate system):像素坐标系是最终图像上的坐标系,用于描述图像中像素的位置。在像素坐标系中,图像被划分为离散的像素格子,每个像素格子都有一个唯一的坐标。
综合一下上面的变换,咱们就有:

这些坐标系之间的转换和变换关系是成像管道中的关键步骤。例如,从世界坐标系到摄像头坐标系的转换涉及相机的外部参数(位置和姿态);从摄像头坐标系到视网膜坐标系的转换涉及相机的内部参数(焦距、主点位置等);从视网膜坐标系到像素坐标系的转换涉及图像分辨率和像素尺寸等。这些转换关系决定了物体在图像中的投影位置和姿态。
通过建立这些坐标系及其之间的转换关系,可以更好地理解和控制图像形成过程。这对于摄像头标定、姿态估计、虚拟现实等计算机视觉和图形学任务非常重要。
然后我们要解决切向失真的问题:

在摄像头成像过程中,常常会出现切向失真会影响图像的几何形状和视觉质量.
切向失真(Tangential distortion):切向失真是由于摄像头透镜与图像平面之间不平行引起的。它会导致图像中的直线看起来弯曲或倾斜。为了校正切向失真,通常需要进行摄像头的切向失真校正。这可以通过详细的光学模型和逆向几何变换来实现。就像是下图:

接下来是摄像头标定算法的通用框架
摄像头标定算法的通用框架

很重要的一张图....
这个优化问题描述了相机标定的过程,目标是通过最小化误差函数来优化相机的内部和外部参数。下面对其中的符号和步骤进行详细解释:
符号解释:
- M:校准板图像的数量。
- N:每个图像上的交叉点数量。
- i:图像的索引,取值范围为1到M。
- j:交叉点的索引,取值范围为1到N。
- Cij:图像中第i个交叉点的像素坐标(投影坐标)。
- Zi:图像中第i个交叉点的世界坐标(校准板上的物理坐标)。
- Θ:需要优化的参数向量。
步骤解释:
1. 根据相机的内部参数,构建相机的内参矩阵K。内参矩阵K包含了相机的焦距、主点位置和像素尺寸等信息。
2. 对于每个图像i和交叉点j,计算其在图像上的投影坐标Cij(像素坐标)。这个投影坐标可以通过相机的外部参数(旋转矩阵R和平移向量t)以及相机的内参矩阵K进行计算。具体而言,根据世界坐标Zi、旋转矩阵R和平移向量t,可以将世界坐标变换到相机坐标系,然后通过内参矩阵K将相机坐标变换到像素坐标。
3. 定义误差函数,即图像中所有交叉点的投影误差之和。这个误差函数衡量了标定参数的准确性,我们的目标是最小化这个误差函数。
4. 通过求解最小化误差函数的优化问题,得到最优的参数向量Θ。这可以通过不同的优化算法(如最小二乘法、非线性优化等)来实现。
在优化过程中,参数向量Θ包含了相机的内部参数(焦距、主点位置和像素尺寸)以及外部参数(旋转矩阵R和平移向量t)。通过优化这些参数,可以获得更准确的相机模型,从而提高相机标定的精度和稳定性。
需要注意的是,这个优化问题是一个非线性优化问题,通常需要使用迭代算法进行求解。在实际应用中,常常使用已知的校准板上的交叉点位置作为已知参数,然后通过优化算法来求解相机的内部和外部参数。这样可以得到一个准确的相机模型,用于后续的图像处理和计算机视觉任务。
初始标定参数的粗略估计
这一步的任务是-给我们一组M张平面校准板的图像,估计相机的内在(除了与失真有关的)和拍摄每张图像时相机姿态的外在
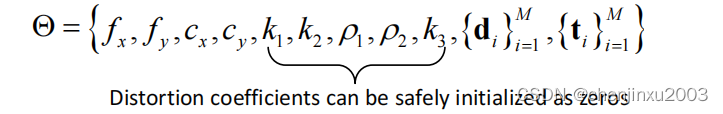
首先失真参数可以标成0,因此,在对其他参数的初始估计时,我们使用成像模型而不考虑畸变
在进行相机标定之前,通常需要对相机的内部参数和外部参数进行粗略的估计,以提供一个初始的起点。这些粗略估计可以通过以下方法获得:
1. 焦距估计:可以使用相机制造商提供的技术规格或文档中给出的焦距估计。如果没有相关信息可用,可以通过测量相机成像的物体尺寸来估计焦距。例如,将一个已知大小的物体放在已知距离处,然后测量物体在图像中的尺寸,通过物体实际尺寸与图像中的尺寸的比例,可以估计焦距。
2. 主点位置估计:主点是图像平面上的光学中心,通常位于图像的中心。可以通过将相机对准一个均匀背景并拍摄一张图像,然后通过计算图像中心位置来估计主点位置。

3. 像素尺寸估计:像素尺寸是图像平面上相邻像素之间的物理距离。可以通过相机制造商提供的技术规格或文档中给出的像素尺寸估计。如果没有相关信息可用,可以通过测量已知物体在图像上的像素距离,并除以物体的实际尺寸来估计像素尺寸。
4. 外部参数估计:外部参数包括相机的旋转矩阵R和平移向量t。可以通过使用惯性测量单元(Inertial Measurement Unit,IMU)或其他传感器来估计相机的姿态信息。这些传感器可以提供相机的旋转和平移信息,从而用于估计外部参数。
然后PPT就开始讲他的灭点了...话说灭点的作用到底是啥啊....
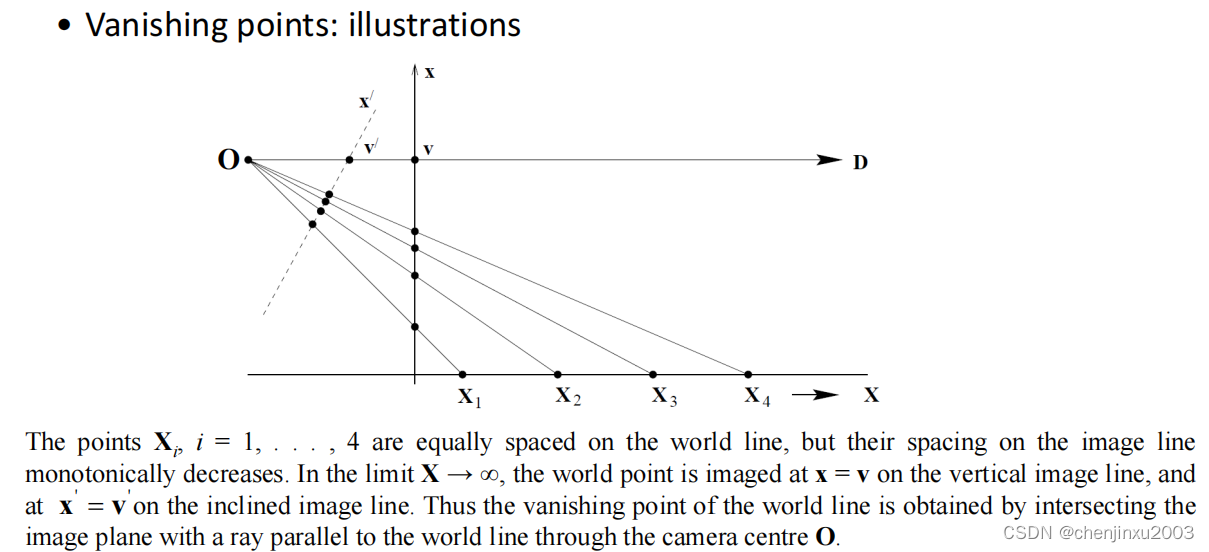
在透视投影中,一个重要的特征是无限远处的物体在图像中可以具有有限的范围。例如,一个无限远处的场景线会被成像为一条以消失点为终点的线。
平行的世界线,比如铁轨线,会被成像为会汇聚的线,并且它们的图像交点就是该铁轨方向的消失点。
消失点:世界线l的消失点可以通过将与l平行且通过相机光心的射线与成像平面相交来获得。换句话说,消失点是世界线l的无穷远点在成像平面上的投影。
另一种定义是,世界线l的消失点是l的无穷远点在成像平面上的投影。
消失点是透视投影中的重要概念,它们提供了关于场景的深度和空间结构的信息。通过在图像中识别和分析消失点,我们可以推断出场景中的平行线、平面和空间方向。这对于计算机视觉中的许多应用非常有用,比如图像校正、物体检测和三维重建等。
需要注意的是,消失点的数量取决于场景中平行线的数量和方向。对于具有多个平行线方向的场景,可能会存在多个消失点。消失点的位置可以通过几何计算或使用计算机视觉算法来确定。
两条平行的世界线应该有相同的无穷点;对于每条线,它的消失点是其无穷点的图像;因此,两条平行世界线的图像会收敛到相同的消失点

然后是如果我们有M个校准板图像,我们最终可以有2个M个这样的方程,在这里我们能解出来fx和fy

需要注意的是,这些粗略估计只是一个初始的起点,可能存在一定的误差。在进行相机标定时,这些估计值将作为初始参数,然后通过优化算法进行迭代优化,以得到更准确的相机内部和外部参数。标定板上已知的交叉点位置也提供了一些准确的信息,有助于提高标定的精度。
此外,还可以使用多个不同角度和距离下的图片进行标定,以增加估计参数的准确性。通过使用多个图片,可以获得更多的约束条件,从而提高标定结果的精度和稳定性。
非线性最小二乘法
这位更是重量级,老师专门分了一篇PPT来讲...
与他相关的东西太多了,也正常
首先讲一下基本概念:
最小二乘法是一种常用的参数估计方法,用于拟合数据并找到最佳拟合曲线。它的目标是通过最小化观测值与拟合值之间的残差平方和,来寻找一个最优的参数组合。
在最小二乘法中,我们假设观测值与拟合值之间存在一个线性关系。假设我们有一组观测数据,其中每个观测值由自变量(通常表示为 x)和因变量(通常表示为 y)组成。我们希望通过拟合一条直线(或更一般的曲线),来描述自变量与因变量之间的关系。
最小二乘法的基本思想是,通过调整直线(或曲线)的斜率和截距,使得拟合值与观测值之间的残差平方和最小化。残差是观测值与拟合值之间的差异,在最小二乘法中通常用误差平方和来度量。通过最小化误差平方和,我们可以得到最佳的拟合曲线,使得观测值与拟合值的差异最小。
最小二乘法的求解通常涉及到求解一个最小化目标函数的优化问题。对于线性回归问题,最小二乘法可以直接求解出最优的参数估计值。对于非线性回归问题,最小二乘法通常需要使用迭代算法(如梯度下降法)来逐步优化参数估计值。
最小二乘法在统计学、经济学、工程学等领域广泛应用,用于拟合数据、回归分析、参数估计等。它是一种简单而强大的方法,可以从数据中提取有关变量之间关系的信息,并用于预测和推断。

首先咱们知道,最小二乘法的一个作用就是求一个函数的局部最小值,然后咱们又知道,计算机视觉里很多情况(不如说所有情况下)咱们都是使用的矩阵,所以咱们这个部分就涉及矩阵的求导了:
我们考虑一个函数 F(x) ,其中 x 是一个 n 维向量。假设 F(x) 是可微的(即具有一阶偏导数)且足够光滑,我们可以使用泰勒展开来逼近函数 F(x)。
泰勒展开是将一个函数在某个点附近用多项式来逼近的方法。对于 F(x) ,我们可以使用泰勒展开来近似表示为:
F(x + h) ≈ F(x) + ∇F(x)⋅h + 1/2 hᵀH(x)h
其中 ∇F(x) 是 F(x) 的梯度向量, H(x) 是 F(x) 的 Hessian 矩阵, h 是一个 n 维向量。
在上述展开式中,第一项 F(x) 是函数在点 x 处的值,第二项 ∇F(x)⋅h 是函数在点 x 处的梯度与向量 h 之间的点积,第三项 1/2 hᵀH(x)h 是函数在点 x 处的 Hessian 矩阵与向量 h 之间的二次型。
这个泰勒展开式的目的是通过将函数 F(x) 近似为一个多项式,以便在给定的点附近进行分析和计算。展开式中的高阶项可以提供更多关于函数的曲率和变化率的信息。
在实际应用中,泰勒展开经常被用于优化问题中的局部近似和数值计算。根据需要,我们可以截取展开式中的一部分,例如只保留一阶项(线性近似)或二阶项(二次近似),以获得更简单或更准确的近似结果。如下图:

这就是所谓的梯度矩阵(一阶),和海森矩阵(二阶)(Hessian 矩阵的第 (i, j) 个元素是函数 F(x) 对变量 xᵢ 和 xⱼ 的二阶偏导数)

这里讲的东西实际上很简单,上面是想说,如果x是一个极小值点,那么这个点的一阶导为0,下面就是想说一阶导为0的地方是函数的驻点,需要注意的是,驻点并不一定是极值点,它也可能是函数的鞍点或其他类型的驻点。要确定一个驻点是否为极值点,通常需要进一步分析 Hessian 矩阵的性质,如特征值的符号(什么高中问题)
然后我们就能得出第二个结论:

定理2:局部极小值的充分条件
假设 xs 是一个驻点,并且 F''(xs) 是正定的,那么 xs 是一个局部极小值点。
如果 F''(xs) 是负定的,那么 xs 是一个局部极大值点。
如果 F''(xs) 是不定的(即同时存在正负特征值),那么 xs 是一个鞍点。
根据定理2的充分条件,当在一个驻点 xs 处,Hessian 矩阵 F''(xs) 的性质满足特定条件时,我们可以确定 xs 是一个局部极小值点、局部极大值点或鞍点。
如果 Hessian 矩阵 F''(xs) 是正定的,意味着它的所有特征值都是正的,那么 xs 是一个局部极小值点。在这种情况下,函数 F 在 xs 处的二阶导数是正的,表明函数曲率向上,函数在 xs 附近呈现凹形状,因此 xs 是一个局部极小值点。
如果 Hessian 矩阵 F''(xs) 是负定的,意味着它的所有特征值都是负的,那么 xs 是一个局部极大值点。在这种情况下,函数 F 在 xs 处的二阶导数是负的,表明函数曲率向下,函数在 xs 附近呈现凸形状,因此 xs 是一个局部极大值点。
如果 Hessian 矩阵 F''(xs) 是不定的,即它既有正特征值又有负特征值,那么 xs 是一个鞍点。在这种情况下,函数 F 在 xs 处的二阶导数既有正值又有负值,表明函数在不同方向上呈现凹凸不一致的形状,因此 xs 是一个鞍点。
这里做一个小tips吧:"
在线性代数中,正定和负定是用来描述矩阵的特征值的性质的术语。
1. 正定矩阵:一个对称矩阵 A 被称为正定的,如果对于任意非零向量 x,都有 x^T A x > 0,其中 x^T 表示向量 x 的转置。换句话说,正定矩阵的所有特征值都是正的。
2. 负定矩阵:一个对称矩阵 A 被称为负定的,如果对于任意非零向量 x,都有 x^T A x < 0。换句话说,负定矩阵的所有特征值都是负的。
正定和负定的概念可以推广到非对称矩阵的情况,但在定理中通常提到的是对称矩阵的情况,因为 Hessian 矩阵是对称矩阵。
在定理2中,当 Hessian 矩阵 F''(xs) 是正定的时候,意味着它的所有特征值都是正的,这表明函数在 xs 处呈现凹形状,从而 xs 是一个局部极小值点。相反,当 Hessian 矩阵是负定的时候,它的所有特征值都是负的,这表明函数在 xs 处呈现凸形状,从而 xs 是一个局部极大值点。
需要注意的是,正定和负定都是关于二次型的性质,它们与函数的凹凸性质相关。在优化问题中,正定和负定的 Hessian 矩阵通常被用作判断局部极值点的条件。
"
那么我们该如何得到这些神奇的点呢?这里我们就要用到各种下降法了:


天哪我们似乎有第三个定义了,那就是经典的梯度下降(),最快下降方向
然后是我们具体的几种办法,有两步的有一步的:

2-阶段方法(Two-phase methods)是一种通用的算法框架,下面是一个名为“2-阶段下降法”(2-phase Descent Method)的算法框架的示例:

通过这个通用框架,可以实现不同的2-阶段下降方法。具体来说,第一阶段通常用于确定一个合适的下降方向,而第二阶段则用于迭代下降至最优解。
那么要讲的第一种办法就是最速梯度下降法:

需要注意的是,最速梯度下降算法框架中并没有明确的终止准则,因此在实际应用中,可以根据需要添加合适的终止条件,例如达到一定的误差精度或迭代次数的上限。此外,还可以根据问题的特点进行一些改进,如使用动态步长调整策略、加入正则化项等。
第二种办法就是牛顿法:
牛顿法(Newton's Method)是一种用于求解优化问题或方程根的迭代算法。它利用函数的二阶导数信息来逼近函数的局部特性,以更快地收敛到最优解或方程的根。
下面是牛顿法的详细步骤:
输入: 初始解 x0, 终止准则, 最大迭代次数
1. 设置迭代计数器 k = 0,解 x = x0
2. 在迭代次数未达到最大次数且未满足终止准则之前,重复以下步骤:
2.1 计算当前解的函数值 f(x) 和一阶导数值 g(x):f(xk) 和 gk = ∇f(xk)
2.2 计算当前解的二阶导数值 H(x):Hk = ∇²f(xk)
2.3 解线性方程系统 Hk * dk = -gk,其中 dk 是牛顿方向
2.4 更新解:x = x + dk
2.5 增加迭代计数器:k = k + 1
2.6 检查终止准则,如果满足则停止迭代;否则返回步骤2继续迭代
3. 返回最终解 x
牛顿法的核心思想是使用当前解的二阶导数(Hessian 矩阵)来近似函数的局部特性,并求解线性方程系统来得到下降方向。由于牛顿法利用了二阶导数信息,因此通常能够更快地收敛到最优解。然而,牛顿法也有一些限制,例如计算和存储二阶导数的成本较高,并且在某些情况下可能会出现数值稳定性问题。
在实际应用中,牛顿法可以用于优化问题的最小化,其中目标是最小化一个可微函数。此外,牛顿法也可以用于求解非线性方程的根,其中目标是找到函数的零点。
需要注意的是,在实际应用中,为了提高数值稳定性和收敛性,通常会采用牛顿法的变种,如改进的牛顿法(如拟牛顿法)或牛顿法的截断版本(如LM算法)。这些变种方法在牛顿法的基础上进行了改进和优化,以克服一些潜在的问题。
然后是一步的方法,实际上就是阻尼法和最信任模型法:
阻尼法(Damped Methods)和信任模型法(Trust Region Methods)是两种常用的优化算法,用于解决非线性优化问题。它们都基于近似模型来进行优化,但采用了不同的策略来控制迭代步长和更新方向。
1. 阻尼法(Damped Methods):
阻尼法通过引入阻尼因子(damping factor)来限制每次迭代的步长,以避免迭代过程中出现过大的步长导致算法不稳定。阻尼因子可以是一个固定的常数或根据迭代过程中的条件动态调整。
具体步骤如下:
- 计算当前解的函数值 f(x) 和一阶导数值 g(x)。
- 计算近似模型 L(x+h)。
- 根据近似模型 L(x+h) 和当前解的函数值 f(x) 进行比较,确定是否接受更新。
- 如果接受更新,更新解:x = x + h;否则,调整阻尼因子,并重新计算近似模型 L(x+h),然后继续迭代。
阻尼法的优点是相对简单且易于实现,但可能会导致收敛速度较慢。
2. 信任模型法(Trust Region Methods):
信任模型法通过在每次迭代中定义一个信任域(trust region)来限制迭代步长,并根据信任域内的模型质量来决定是否接受更新。信任域是一个在当前解附近定义的区域,其中模型与真实函数的行为相对一致。
具体步骤如下:
- 计算当前解的函数值 f(x) 和一阶导数值 g(x)。
- 构建近似模型 L(x+h)。
- 在信任域内解决子问题,确定在信任域范围内的最优更新步长。
- 根据子问题的解和信任域范围来更新解。
- 根据实际更新和近似模型的改进情况,调整信任域的大小。
信任模型法的优点是可以更灵活地控制迭代步长,并在每次迭代中根据近似模型的质量进行自适应调整。然而,信任域的定义和调整可能需要更多的计算和参数调整。
需要注意的是,具体的阻尼法和信任模型法的实现和细节取决于具体的优化算法和问题要求。这些方法可以根据具体情况进行调整和改进,以获得更好的收敛性和性能。
讲完了这些之后就是:

解决非线性方法的几个小概念:
非线性最小二乘问题(Non-linear Least Squares Problems)是指形式为最小化残差平方和的优化问题,其中残差是一个非线性函数关于未知参数的函数。这类问题在许多实际应用中广泛存在,如曲线拟合、参数估计等。
下面是对这些问题中常用的优化方法的简要介绍:
1. 高斯-牛顿法(Gauss-Newton Method):
高斯-牛顿法(Gauss-Newton Method)是一种迭代算法,用于解决非线性最小二乘问题。该算法通过线性化残差函数来近似原始问题,并使用线性最小二乘方法求解线性化问题的近似解。然后,通过迭代更新未知参数,直到满足收敛准则。
下面是高斯-牛顿法的详细步骤:
1. 初始化参数:选择初始参数估计值,例如将参数设置为零向量或根据先验知识进行估计。
2. 迭代过程:
a. 计算残差向量:根据当前的参数估计值计算残差向量,表示观测值与模型预测值之间的差异。
b. 计算雅可比矩阵:计算残差函数关于参数的雅可比矩阵,该矩阵描述了残差对于参数的偏导数。
c. 构建线性方程组:根据雅可比矩阵,构建线性方程组,其中残差向量为右侧的目标向量。
d. 求解线性方程组:使用线性最小二乘方法求解线性方程组,得到参数更新的增量向量。
e. 更新参数:将参数估计值更新为当前参数估计值加上增量向量。
f. 检查收敛准则:检查参数增量的大小是否满足收敛准则。如果满足,则停止迭代;否则,返回步骤(a)继续迭代。
高斯-牛顿法的核心思想是通过线性化残差函数来近似原始问题,将非线性最小二乘问题转化为线性最小二乘问题。在每次迭代中,它使用雅可比矩阵来描述残差对于参数的变化率,并根据线性方程组的解来更新参数估计值。通过迭代更新参数,高斯-牛顿法逐步优化参数,使得残差逐渐减小,从而达到最小化残差平方和的目标。
需要注意的是,高斯-牛顿法对于初始参数的选择非常敏感,不同的初始值可能会导致不同的结果。此外,当参数估计值离最优解较远时,线性化可能会引入较大的误差,从而导致算法无法收敛或收敛到局部最优解。因此,在实际应用中,需要谨慎选择初始参数,并进行适当的收敛准则判断,以获得可靠的结果。
2. 莱文贝格-马夸尔特方法(Levenberg-Marquardt Method):
莱文贝格-马夸尔特方法(Levenberg-Marquardt Method)是一种用于求解非线性最小二乘问题的迭代算法。它综合了高斯-牛顿法和最小化信赖域方法的思想,旨在平衡这两种方法的优点,并提高算法的稳定性。
下面是莱文贝格-马夸尔特方法的详细步骤:
1. 初始化参数:选择初始参数估计值,例如将参数设置为零向量或根据先验知识进行估计。
2. 设置初始阻尼因子:选择一个较小的正数作为初始阻尼因子,用于控制参数更新的步长。通常,初始阻尼因子可以设置为较小的值,例如0.01。
3. 迭代过程:
a. 计算残差向量:根据当前的参数估计值计算残差向量,表示观测值与模型预测值之间的差异。
b. 计算雅可比矩阵:计算残差函数关于参数的雅可比矩阵,该矩阵描述了残差对于参数的偏导数。
c. 构建增广矩阵:根据雅可比矩阵和残差向量构建增广矩阵,其中残差向量为右侧的目标向量。
d. 调整阻尼因子:根据当前的阻尼因子和增广矩阵,计算调整后的阻尼因子。这个调整过程旨在平衡高斯-牛顿法和最小化信赖域方法之间的权衡。如果增广矩阵在数值上近似为正定,可以保持较小的阻尼因子;否则,可以增加阻尼因子的值。
e. 解线性方程组:使用调整后的阻尼因子,求解增广矩阵的线性方程组,得到参数更新的增量向量。
f. 更新参数:将参数估计值更新为当前参数估计值加上增量向量。
g. 检查收敛准则:检查参数增量的大小是否满足收敛准则。如果满足,则停止迭代;否则,返回步骤(a)继续迭代。
莱文贝格-马夸尔特方法通过引入阻尼因子来控制参数更新的步长,并根据增广矩阵的特性动态调整阻尼因子的大小。当增广矩阵近似为正定时,可以保持较小的阻尼因子,使得算法更接近高斯-牛顿法;而当增广矩阵不是正定时,增加阻尼因子的值可以提高算法的稳定性,使其更接近最小化信赖域方法。
莱文贝格-马夸尔特方法相对于高斯-牛顿法的优点是在参数估计值离最优解较远时仍能保持较好的收敛性。它能够处理参数更新步长较大的情况,并且对于初始参数的选择不太敏感。然而,莱文贝格-马夸尔特方法的计算开销较高,因为需要求解增广矩阵的线性方程组。
在实际应用中,莱文贝格-马夸尔特方法常用于非线性最小二乘问题的求解,特别是在参数估计值较远离最优解、存在较大的残差或存在较大的噪声的情况下。它在许多科学和工程领域中都有广泛的应用,例如计算机视觉、机器学习、信号处理和优化问题等。
3. 鲍威尔的狗腿方法(Powell's Dog Leg Method):
鲍威尔的狗腿方法(Powell's Dog Leg Method)是一种用于求解无约束优化问题的迭代算法。它是由鲍威尔(Powell)在1964年提出的,旨在寻找函数的局部最小值。
下面是鲍威尔的狗腿方法的详细步骤:
1. 初始化参数:选择初始参数估计值,例如将参数设置为零向量或根据先验知识进行估计。
2. 迭代过程:
a. 计算负梯度:计算当前参数估计值处的负梯度向量,表示函数在该点的下降方向。
b. 计算海森矩阵:计算当前参数估计值处的海森矩阵,用于描述函数的二阶导数信息。
c. 判断步长:根据负梯度和海森矩阵,判断是否可以通过沿负梯度方向一步到达最优解。如果可以,则计算最优步长并更新参数估计值;否则,进行下一步。
d. 计算狗腿步长:当无法通过沿负梯度方向一步到达最优解时,计算狗腿步长。狗腿步长是一个介于最速下降法步长和牛顿法步长之间的步长,旨在综合两者的优点。
e. 更新参数:根据计算得到的狗腿步长,更新参数估计值。
f. 检查收敛准则:检查参数的变化是否满足收敛准则。如果满足,则停止迭代;否则,返回步骤(a)继续迭代。
鲍威尔的狗腿方法结合了最速下降法和牛顿法的思想。当负梯度方向可以直接指向最优解时,使用最速下降法的步长;当负梯度方向不再适用时,使用牛顿法的步长。通过综合利用这两种步长,狗腿方法在迭代过程中能够更快地接近最优解。
需要注意的是,鲍威尔的狗腿方法需要计算海森矩阵,而海森矩阵的计算成本较高,特别是在参数较多的情况下。因此,在实际应用中,为了降低计算复杂度,通常采用近似的海森矩阵或其他替代方法来估计步长。
鲍威尔的狗腿方法在无约束优化问题中具有较好的收敛性和全局收敛性。它被广泛应用于优化问题,特别是在需要求解高维问题或具有复杂非线性结构的问题时。
好的又到了我们的小tip时间:"
到底啥是残差向量残差函数呢?
在数学和优化问题中,残差函数是指描述实际观测值与模型预测值之间差异的函数。在最小二乘问题中,残差函数通常是指观测值与模型预测值之间的差异的平方和。
假设我们有一组观测数据,其中每个观测数据由自变量和因变量组成。我们使用一个模型来预测因变量的值。残差函数衡量了每个观测值的预测值与实际观测值之间的差异。
残差函数的残差向量是一个向量,其中的每个元素表示对应观测值的残差。假设有 n 个观测数据,那么残差向量的长度为 n。
以最小二乘问题为例,假设有 n 个观测数据 (x_i, y_i),其中 x_i 是自变量,y_i 是因变量。我们使用一个模型来预测因变量的值,表示为 f(x_i;θ),其中 θ 是模型的参数。那么残差函数可以定义为:
R(θ) = [y_1 - f(x_1;θ), y_2 - f(x_2;θ), ..., y_n - f(x_n;θ)]
这里的 R(θ) 表示残差向量,其中的每个元素是对应观测值的残差。我们的目标是通过调整参数 θ 来最小化残差向量的范数(通常是平方和)。
在最小二乘问题中,我们希望找到一个最优的参数估计值 θ*,使得残差向量的范数最小:
θ* = argmin ||R(θ)||^2
通过最小化残差向量的平方和,我们能够找到最优的参数估计值,使得模型的预测值与观测值之间的差异最小。
残差函数和残差向量在许多优化和拟合问题中都有广泛的应用,例如非线性最小二乘拟合、回归分析和机器学习中的损失函数等。
"
这些方法都是针对非线性最小二乘问题的特定优化方法,用于求解参数估计、曲线拟合等应用。每种方法都有其独特的优点和适用范围,具体选择哪种方法取决于问题的性质和要求。在实际应用中,还可以根据具体情况对这些方法进行优化和改进,以提高收敛性和性能。
鸟瞰图生成
好像老师还没讲...之后再更新吧