一、介绍
泰勒级数是数学中的一个基本概念,在机器学习领域有着重要的应用。本文将探讨泰勒级数的基础知识、它在机器学习中的相关性以及一些具体应用。

揭开复杂性:利用泰勒级数增强机器学习应用的理解和效率。
二、理解泰勒级数
在数学中,泰勒级数或函数的 a> 广泛使用了这种特殊情况18世纪中叶的泰勒级数。 Colin Maclaurin 当 0 是考虑导数的点时,麦克劳林级数命名,他于 1715 年提出了泰勒级数。泰勒级数也称为布鲁克·泰勒。对于大多数常见函数,该函数及其泰勒级数之和在该点附近相等。泰勒级数以表示的项的无限总和以函数在单个点的导数是一个 泰勒展开式
由第一个 n + 形成的 部分和 1 泰勒级数的项是 多项式 次数 n。这意味着该函数在区间(或圆盘)的每个点都是解析的。 x)包含复平面 开盘(或开区间。即使函数的泰勒级数是收敛的,函数也可能与其泰勒级数之和不同。如果函数等于其泰勒级数在某些无限序列 泰勒多项式的极限,则其和为收敛给出了对使用此类近似所引入的误差的定量估计。如果函数的泰勒级数泰勒定理 的增加而变得更加准确。 n 的功能。泰勒多项式是函数的近似值,通常随着 泰勒多项式第 n 称为
泰勒级数是将函数表示为根据单点导数值计算得出的无穷项之和。它是数学分析中的强大工具,有助于用多项式逼近复杂函数。最简单的形式是,对于函数 f(x),关于点 a 的泰勒级数由下式给出:
f(x)=f)3+…a−x)(a′′′(f)2+3 !a−x′(< /span>a′′(f)+2!a −x)(af)+a(
三、机器学习中的泰勒级数
在机器学习中,泰勒级数用于多种目的,例如优化算法、逼近函数和理解模型的行为。
3.1. 优化
泰勒级数在机器学习中最常见的应用之一是优化问题。许多机器学习算法,尤其是深度学习算法,都涉及优化成本函数以找到最佳模型参数。泰勒级数可用于近似这些函数,从而更容易计算梯度和执行优化,例如在梯度下降算法中。
3.2. 函数逼近
机器学习通常涉及根据给定数据估计未知函数。泰勒级数可以使用更简单的多项式形式来近似复杂函数,这在回归分析等算法中特别有用。
3.3. 理解模型行为
泰勒级数还可用于理解和解释机器学习模型的行为。通过围绕一个点扩展模型的功能,我们可以深入了解输入的变化如何影响输出,这对于特征重要性分析和调试模型等任务至关重要。

四、具体应用
- 神经网络训练:在训练神经网络时,反向传播算法经常使用泰勒级数来计算权重梯度。
- 正则化技术:机器学习中的一些正则化技术(例如 Tikhonov 正则化)可以使用泰勒级数展开来理解和导出。
- 非线性模型:对于非线性模型,泰勒级数提供了一种围绕点对模型进行线性化的方法,这对于分析和优化非常有用。
- 算法开发:高级机器学习算法(例如高斯过程和一些集成方法)有时会使用泰勒级数进行开发和细化。
五、代码
创建一个完整的 Python 示例来演示泰勒级数在机器学习中的使用可能非常有启发性。对于此示例,让我们创建一个合成数据集,将泰勒级数近似应用于函数,并使用绘图可视化结果。
我们将:
- 生成合成数据集。
- 定义一个非线性函数,我们将使用泰勒级数对其进行近似。
- 对此函数应用泰勒级数近似。
- 可视化原始函数及其泰勒级数近似值。
让我们从编写 Python 代码开始:
import numpy as np
import matplotlib.pyplot as plt
# 1. Generate a synthetic dataset
np.random.seed(0)
x = np.linspace(-2, 2, 100)
y = np.sin(x) + np.random.normal(0, 0.1, x.shape) # Using sine function with some noise
# 2. Define the non-linear function (e.g., sine function)
def original_function(x):
return np.sin(x)
# 3. Apply Taylor Series approximation (up to 3rd degree for simplicity)
def taylor_series_approximation(x, a=0, n=3):
approximation = 0
for i in range(n+1):
term = (np.math.factorial(i))**-1 * np.sin(a) * (x - a)**i
approximation += term
return approximation
# Taylor Series approximation around 0
taylor_approx = taylor_series_approximation(x, a=0, n=3)
# 4. Visualize the original function and its Taylor approximation
plt.figure(figsize=(10, 6))
plt.scatter(x, y, color='blue', label='Synthetic Data')
plt.plot(x, original_function(x), label='Original Function', color='green')
plt.plot(x, taylor_approx, label='Taylor Series Approximation', color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Original Function vs. Taylor Series Approximation')
plt.legend()
plt.show()在此代码中:
- 我们使用添加高斯噪声的正弦函数创建一个合成数据集。
original_function是我们将近似的正弦函数。taylor_series_approximation函数计算正弦函数的泰勒级数近似值。- 最后,我们绘制原始函数、近似值和合成数据点。
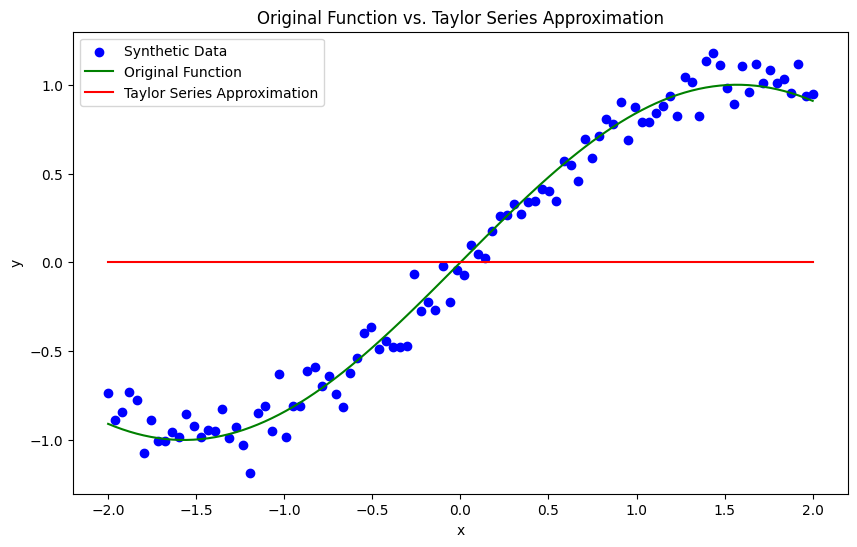
您可以在安装了 numpy 和 matplotlib 的 Python 环境中运行此代码来查看可视化效果。此示例演示了泰勒级数在类似机器学习的环境中的基本应用,其中我们近似函数并将其与实际数据进行比较。
六、结论
泰勒级数是机器学习领域的多功能且强大的工具。它有助于简化复杂函数、优化算法和理解模型行为。其将函数表示为多项式的能力使其在从神经网络训练到算法开发和模型解释的各种机器学习任务中具有无价的价值。随着机器学习的不断发展,泰勒级数仍然是数据科学家和研究人员工具包中的重要组成部分。