理解DCT与DST【二】：离散余弦变换

本文主要是将先前的博客 离散傅里叶变换DFT、离散余弦变换DCT、离散正弦变换DST，原理与公式推导 从图片修改为 Markdown 脚本，方便读者浏览，同时增加了部分内容。但由于文章字符过多，无法全部放在一篇博客上，所以将之前的文章拆分为三部分，可通过以下链接查看其它部分。

• 理解DCT与DST【一】：离散傅里叶变换
• 理解DCT与DST【三】：离散正弦变换

2 离散余弦变换（Discrete Cosine Transform, DCT）

由 1.5.5 节内容可知，对于有限长对称实序列，其 DFT 序列同样是有限长对称实序列。更重要的是，有限长对称实序列的 DFT 的计算只需要用到序列的一半采样点数据，而且可以转化为只涉及余弦函数的实数运算，简化了 DFT 的计算，这就是离散余弦变换的出发点。

实际上，离散余弦变换对应着非对称有限长实序列的对称延拓序列的离散傅里叶变换的非冗余部分，不同的延拓方式对应着不同的延拓序列长度以及不同的离散傅里叶变换系数，因此也就对应着不同的离散余弦变换系数。根据 1.5.6 节的分析，离散傅里叶变换系数中的非冗余部分即独立分量的个数与原序列中的独立分量个数是一致的，因此离散余弦变换系数的个数也就对应着延拓序列中独立分量的个数。

数学上离散余弦变换总共定义了 8 种形式，对应着 8 种有限长非对称实序列的对称延拓方式，分别用 DCT-I ~ DCT-VIII 来表示。在 H.266 视频编解码标准中，主要用到了 DCT-II 和 DCT-VIII，下面主要对这两种 DCT 进行推导和分析，其他类型的 DCT 只给出相应的延拓方式和对应的公式定义。

作为示例，假设有长度 $N=3$ 的有限长非对称实序列 $x[n]:4,1,3;n=0,1,2$，如图 2-1 所示，后面的分析都将基于该序列进行展开。

图 2-1 原始有限长实序列

2.1 DCT-II

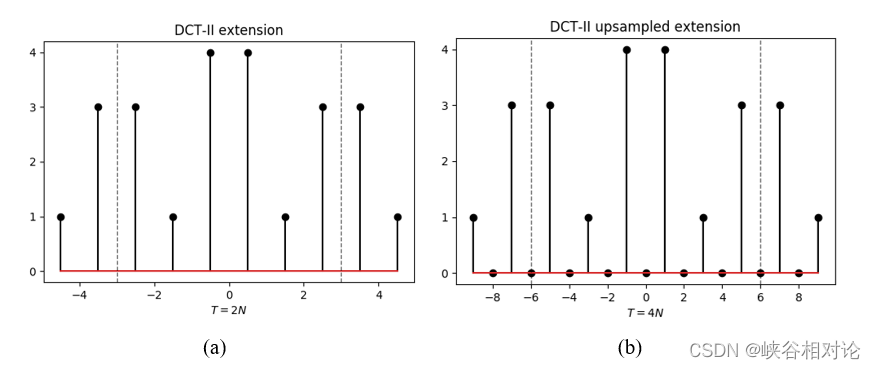
图 2-1 所示的有限长非对称实序列 $x[n]$ 的 DCT-II 对称及周期延拓如图 2-2(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，而离散序列在计算机内都是以整数索引存储的，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 2-2(b) 所示。准确来说，延拓序列的公式化定义如式（2-1）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。

$$\tilde{y}[m+4kN]=\tilde{x}\left[\frac{|m|-1}{2}\right],m=-2N,-2N+1,...,2N-1.\text{\hspace{1em}(2-1)}$$

那么有限长对称实序列 $y[m]$ 的长度为 $4N$，而独立分量只有 $N$ 个，可以预见对应 DFT 的独立分量也只有 $N$ 个。

图 2-2 DCT-II 延拓（a）及其插零上采样（b）
图 2-3 DCT-II 延拓序列的 DFT 序列

根据前面的内容，可以得到 $y[m]$ 的 $4N$ 点 DFT 为

$$\begin{array}{rl}\tilde{Y}[l]& =\sum _{m=-2N}^{2N-1}\tilde{y}[m]e^{-j\frac{2\pi lm}{4N}}=\sum _{m=1}^{2N-1}y[m]\left[e^{-j\frac{\pi lm}{2N}}+e^{j\frac{\pi lm}{2N}}\right]\\ & =2\sum _{m=0}^{2N-1}y[m]\cos \left[\frac{\pi lm}{2N}\right]=2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(2n+1\right)}{2N}\right]\end{array}\text{\hspace{1em}(2-2)}$$

进一步，我们可以得到以下性质，

$$\begin{array}{rl}\tilde{Y}[l+2N]& =2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(l+2N\right)\left(2n+1\right)}{2N}\right]\\ & =2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(2n+1\right)}{2N}+\pi \left(2n+1\right)\right]\\ & =-2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(2n+1\right)}{2N}\right]=-\tilde{Y}[l]\end{array}\text{\hspace{1em}(2-3)}$$

$$\begin{array}{c}\tilde{Y}[l]=\tilde{Y}[-l]\\ \tilde{Y}[2N-l]=\tilde{Y}[l-2N]=\tilde{Y}[l+2N]=-\tilde{Y}[l]\\ \tilde{Y}[N]=\tilde{Y}[2N-N]=-\tilde{Y}[N]\Rightarrow \tilde{Y}[N]=0\end{array}\text{\hspace{1em}(2-4)}$$

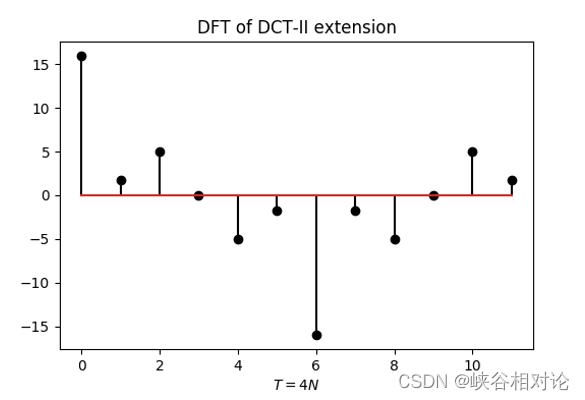
因此，有限长对称实序列 $y[m]$ 的$4N$ 点 DFT 中的独立分量确实只有 $N$ 个。作为示例，图 2-2(b) 中定义的延拓序列的 DFT 如图 2-3 所示。根据以上性质，可以得到其逆变换为

$$\begin{array}{rl}y[m]& =\frac{1}{4N}\sum _{l=0}^{4N-1}Y[l]e^{j\frac{2\pi lm}{4N}}=\frac{1}{4N}\sum _{l=0}^{2N-1}Y[l]\left[e^{j\frac{2\pi lm}{4N}}-e^{j\frac{2\pi \left(2N+l\right)m}{4N}}\right]\\ & =\frac{1}{4N}\left[1-{\left(-1\right)}^m\right]\cdot \sum _{l=0}^{2N-1}Y[l]e^{j\frac{\pi lm}{2N}}\\ & =\frac{1}{4N}\left[1-{\left(-1\right)}^m\right]\cdot \left\{\sum _{l=1}^{N-1}Y[l]\left[e^{j\frac{\pi lm}{2N}}-e^{j\frac{\pi \left(2N-l\right)m}{2N}}\right]+Y[0]\right\}\\ & =\frac{1}{4N}\left[1-{\left(-1\right)}^m\right]\cdot \left\{\sum _{l=1}^{N-1}Y[l]\left[e^{j\frac{\pi lm}{2N}}-{\left(-1\right)}^m{e}^{-j\frac{\pi lm}{2N}}\right]+Y[0]\right\}\\ & =\frac{1}{4N}\left[1-{\left(-1\right)}^m\right]\cdot \left[\sum _{l=1}^{N-1}Y[l]\left(e^{j\frac{\pi lm}{2N}}+e^{-j\frac{\pi lm}{2N}}\right)+Y[0]\right]\\ & =\frac{1}{2N}\left[1-{\left(-1\right)}^m\right]\cdot \sum _{l=0}^{N-1}{\epsilon }_{l}Y[l]\cos \left(\frac{\pi lm}{2N}\right)\end{array}\text{\hspace{1em}(2-5)}$$

其中

$${\epsilon }_l=\{\begin{array}{cc}\frac{1}{2},& l=0\\ 1,& l\ne 0\end{array}.$$

由此，定义 DCT-II 的计算公式如下，

$$\begin{array}{c}X[k]=DC{T}_2\left[x[n]\right]=Y[k]=2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi k\left(2n+1\right)}{2N}\right]\\ x[n]=IDC{T}_2\left[X[k]\right]=y[2n+1]=\frac{1}{N}\sum _{k=0}^{N-1}{\epsilon }_{k}X[k]\cos \left[\frac{\pi k\left(2n+1\right)}{2N}\right]\\ wheren,k=0,1,...,N-1\end{array}\text{\hspace{1em}(2-6)}$$

可以看到，DCT-II 与由式（2-1）所定义延拓序列的 DFT 是对应的，但只包含了部分分量。为了公式的一致性，将式（2-6）的系数平均分配到两边，则有

$$\begin{array}{c}X[k]=DC{T}_2\left[x[n]\right]=\sqrt{\frac{2}{N}}{\epsilon }_k\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi k\left(2n+1\right)}{2N}\right]\\ x[n]=IDC{T}_2\left[X[k]\right]=\sqrt{\frac{2}{N}}{\epsilon }_k\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi k\left(2n+1\right)}{2N}\right]\\ wheren,k=0,1,...,N-1\end{array}\text{\hspace{1em}(2-7)}$$

逆变换这里 ${\epsilon }_k$ 写在了求和符号前面，主要是为了表达与正变换公式的一致性，严谨的话应该放在求和符号里面。注意此时

$${\epsilon }_k=\{\begin{array}{cc}\frac{1}{\sqrt{2}},& k=0\\ 1,& k\ne 0\end{array}.$$

写成矩阵形式，则有

$$\begin{array}{c}\mathbf{X}=\mathbf{Ax},\mathbf{x}={\mathbf{A}}^T\mathbf{X}\Rightarrow \mathbf{X}=\mathbf{A}{\mathbf{A}}^T\mathbf{X}\Rightarrow \mathbf{A}{\mathbf{A}}^T=\mathbf{I}\Rightarrow {\mathbf{A}}^T={\mathbf{A}}^{-1}\\ \mathbf{A}\in {\mathbb{R}}^{N\times N},A_{kn}=\sqrt{\frac{2}{N}}{\epsilon }_k\cos \left[\frac{\pi k\left(2n+1\right)}{2N}\right]\end{array}\text{\hspace{1em}(2-8)}$$

这意味着变换矩阵 $\mathbf{A}$ 是正交矩阵，也就是说式（2-7）定义的离散余弦变换与逆变换属于正交变换。那么，矩阵 $\mathbf{A}$ 的每一行或者每一列都是线性无关的，时域或空域的离散信号序列 $\mathbf{x}$ 可以表示为矩阵 $\mathbf{A}$ 行向量的转置 ${\mathbf{a}}_n$ 关于离线余弦变换系数 $X[k]$ 的线性组合，如式（2-9）所示，这些向量 ${\mathbf{a}}_n$ 组成了一个规范正交基，每个基向量代表着信号不同的变化频率，例如 $k=0$ 时代表了直流分量，$k$ 越大，信号变化的频率越快，这时称为交流分量，这与傅里叶变换的分析是类似的。

$$\begin{array}{c}{\mathbf{a}}_k={\left[\begin{array}{cccc}{A}_{k0}& A_{k1}& \cdots & A_{k\left(N-1\right)}\end{array}\right]}^T\\ \mathbf{x}={\mathbf{A}}^T\mathbf{X}=\left[\begin{array}{cccc}{\mathbf{a}}_0& {\mathbf{a}}_1& \cdots & {\mathbf{a}}_{N-1}\end{array}\right]\left[\begin{array}{c}{X}_0\\ X_0\\ ⋮\\ X_{N-1}\end{array}\right]=X_0{\mathbf{a}}_0+X_1{\mathbf{a}}_1+\cdots +X_{N-1}{\mathbf{a}}_{N-1}\end{array}\text{\hspace{1em}(2-9)}$$

拓展到二维信号例如常见的图像信号，在 1.7 节我们证明了二维离散傅里叶变换是可分离的，因此容易证明二维离散余弦变换同样是可分离的，这里不赘述。假设有宽高为 $M\times N$ 的二维信号 $x[m,n]$，令 $\mathbf{P}$，$\mathbf{Q}$ 分别为大小为 $M\times M$ 和 $N\times N$ 的变换矩阵，由 1.7 节内容及前面的分析知，

$$\begin{array}{c}\mathbf{X}={\left(\mathbf{P}{\left(\mathbf{Qx}\right)}^T\right)}^T=\mathbf{Qx}{\mathbf{P}}^T\Rightarrow \mathbf{x}={\mathbf{Q}}^T\mathbf{Qx}{\mathbf{P}}^T\mathbf{P}={\mathbf{Q}}^T\mathbf{XP}\\ \mathbf{x}=\left[\begin{array}{cccc}{\mathbf{q}}_0& {\mathbf{q}}_1& \cdots & {\mathbf{q}}_{N-1}\end{array}\right]\mathbf{X}\left[\begin{array}{c}{\mathbf{p}}_0^T\\ {\mathbf{p}}_1^T\\ ⋮\\ {\mathbf{p}}_{M-1}^T\end{array}\right]=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}X[m,n]{\mathbf{q}}_n{\mathbf{p}}_m^T\\ where\mathbf{P}\in {\mathbb{R}}^{M\times M},\mathbf{Q}\in {\mathbb{R}}^{N\times N}\end{array}\text{\hspace{1em}(2-10)}$$

这时，我们将每个大小 $N\times M$ 的 ${\mathbf{q}}_n{\mathbf{p}}_m^T$ 矩阵称为二维离散余弦变换的基图像，其中 ${\mathbf{p}}_m$ 和 ${\mathbf{q}}_n$ 分别反映了信号水平和垂直的变化频率。那么二维信号 $\mathbf{x}$ 可以表示为这些基图像的线性组合，其权值即为离散余弦变换的系数。而离散余弦变换的各个系数是通过基图像与信号之间的內积求得的，因此刚好又代表了信号与各个基图像之间的相关性或者相似度，即信号与某个基图像越相似，则该基图像对应的离散余弦变换系数就会越大，反之则越小。因此，离散余弦变换是否能把信号的信息尽量压缩到少数几个系数上，关键在于是否能通过少数几个基图像的线性组合来尽可能准确地还原原始的信号。

图 2-4 展示了 $8\times 8$ 的二维 DCT-II 的 64 个基图像。可以看到，左上角的基图像代表了信号的直流分量，此时信号在空间上没有任何变化；而在最上边一行（最左边的一列），其反映了信号在水平（垂直）方向上强度周期变化的特点，且越往右（下）边，信号变化的频率越来越高，从而组成了从宽粗到窄细、从稀疏到密集的各种垂直（水平）线条，而这种模式（pattern）刚好与图像中的纹理细节十分的相像；而在右下角，信号变化的频率越来越高，基图像也越来越表现得像马赛克，相邻像素之间的相关性也越来越低，这种模式又十分符合同分布随机噪声（比如高斯白噪声）的分布特性。因为我们一般关注的是图像的整体亮度以及细节纹理，这恰好使得图像的信息能够大致通过图 2-4 中左上角少数几个基图像的线性组合来表示，所以图 2-4 所代表的 DCT-II 也被广泛应用于图像视频压缩以及降噪当中。但要注意，不同类型的 DCT 由于变换公式不一样，它们所产生的基图像也各不相同，并不是所有类型的 DCT 都能产生如图 2-4 中这种比较规则变化的图形，因此也不是所有类型的 DCT 都能与 DCT-II 相提并论。但相比于 DCT-II，在某些应用场景中，某些 DCT 以及后面会讲述的 DST 类型也会产生一些比 DCT-II 更加符合信号分布的基图像组合。比如在 H.266 中，DCT-VIII 和 DST-VII 在某些情况下相比于 DCT-II 可获得更优的残差变换压缩性能。在文章的末尾，我会给出各种 DCT 类型的基图像给大家作为参考。

根据图 2-4 可以知道，对于水平方向缓慢变化的信号，其 DCT 系数将主要集中在左边垂直方向；而对于垂直方向缓慢变化的信号，其 DCT 系数将主要集中在上边水平方向。在基于预测的图像编码中，例如 H.266，不同的角度预测模式会产生不同的残差分布。例如对于水平预测，水平方向的残差通常会呈现从左到右基本相同或者逐渐逐渐增大的特性，而垂直方向由于各行彼此参考的像素各不相关，从而表现出随机变化的特性，因此对残差进行离散余弦变换后，其 DCT 系数通常会集中在左侧的少数几列，这时配合垂直方向的系数扫描，可以使得系数更加集中，利于后续的熵编码操作。同理，对于其他的预测模式，我们也可以相应采用 Zigzag 扫描或者水平扫描，从而获得更好的压缩特性。

图 2-4 8×8 大小的 DCT-II 基图像

2.2 DCT-VIII

图 2-1 所示的有限长非对称实序列 $x[n]$ 的 DCT-VIII 对称及周期延拓如图 2-5(a) 所示。类似于 DCT-II 延拓，由于序列右移了 1/2，所有采样点都处于非整数索引位置，而离散序列在计算机内都是以整数索引存储的，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 2-5(b) 所示。准确来说，延拓序列的公式化定义如式（2-11）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。

$$\begin{array}{c}\tilde{y}\left[m+k\left(8N+4\right)\right]=\{\begin{array}{lc}\tilde{x}\left[\frac{|m|-1}{2}\right],& \left|m\right|⩽2N\\ 0,& \left|m\right|=2N+1\\ -\tilde{x}\left[\frac{4N+1-|m|}{2}\right],& \left|m\right|⩾2N+2\end{array}\\ wherem=-4N-2,-4N-1,...,4N+1.\end{array}\text{\hspace{1em}(2-11)}$$

图 2-5 DCT-VIII 延拓（a）及其插零上采样（b）
图 2-6 DCT-VIII 延拓序列的 DFT 序列

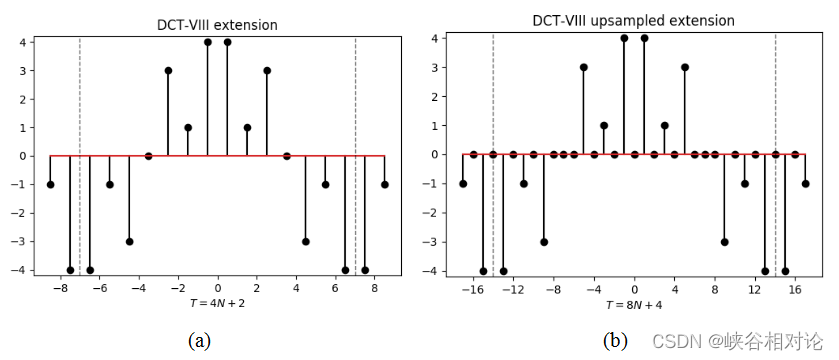
那么，有限长对称实序列 $y[m]$ 的长度为 $8N+4$，而独立分量只有 $N$ 个，因此可以预见其 DFT 的独立分量也只有 $N$ 个。根据前面的内容可得，

$$\begin{array}{rl}\tilde{Y}[l]& =\sum _{m=-4N-2}^{4N+1}\tilde{y}[m]e^{-j\frac{2\pi lm}{8N+4}}\\ & =\sum _{m=1}^{4N+1}y[m]\left(e^{-j\frac{\pi lm}{4N+2}}+e^{j\frac{\pi lm}{4N+2}}\right)\\ & =2\sum _{m=1}^{4N+1}y[m]\cos \left(\frac{\pi lm}{4N+2}\right)\\ & =2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(2n+1\right)}{4N+2}\right]-2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(4N+2-2n-1\right)}{4N+2}\right]\\ & =2\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(2n+1\right)}{4N+2}\right]-2\sum _{n=0}^{N-1}x[n]\cos \left[\pi l-\frac{\pi l\left(2n+1\right)}{4N+2}\right]\\ & =2\left[1-{\left(-1\right)}^l\right]\cdot \sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi l\left(2n+1\right)}{4N+2}\right]\end{array}\text{\hspace{1em}(2-12)}$$

因此，我们可以得到以下性质，

$$\begin{array}{c}\tilde{Y}[2l]=0,\tilde{Y}[l]=\tilde{Y}[-l]\\ \tilde{Y}[l+4N+2]=-\tilde{Y}[l]\\ \tilde{Y}[4N+2-l]=\tilde{Y}[l-4N-2+8N+4]=\tilde{Y}[l+4N+2]=-Y[l]\\ \tilde{Y}[2N+1]=-\tilde{Y}[4N+2-2N-1]=-\tilde{Y}[2N+1]=0\end{array}\text{\hspace{1em}(2-13)}$$

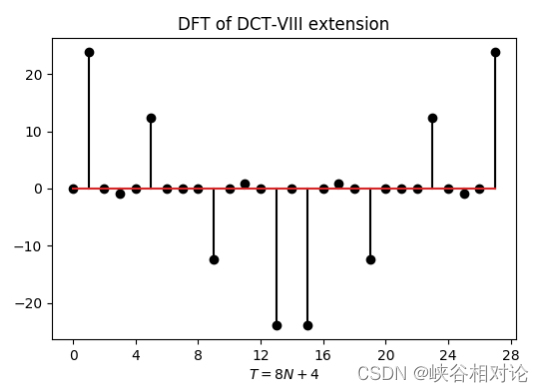
所以，有限长对称实序列 $y[m]$ 的 $8N+4$ 点 DFT 中的独立分量确实只有 $N$ 个。作为示例，图 2-5(b) 中定义的延拓序列的 DFT 如图 2-6 所示。根据以上性质，可以得到其逆变换为

$$\begin{array}{rl}y[m]& =\frac{1}{8N+4}\sum _{l=0}^{8N+3}Y[l]e^{j\frac{2\pi lm}{8N+4}}\\ & =\frac{1}{8N+4}\sum _{l=0}^{4N+1}Y[l]\left[e^{j\frac{2\pi lm}{8N+4}}-e^{j\frac{2\pi \left(4N+2+l\right)m}{8N+4}}\right]\\ & =\frac{1}{8N+4}\left[1-{\left(-1\right)}^m\right]\cdot \sum _{l=0}^{4N+1}Y[l]e^{j\frac{\pi lm}{4N+2}}\\ & =\frac{1}{8N+4}\left[1-{\left(-1\right)}^m\right]\cdot \sum _{l=0}^{N-1}Y[2l+1]\left[e^{j\frac{\pi \left(2l+1\right)m}{4N+2}}-e^{j\frac{\pi \left(4N+2-2l-1\right)m}{4N+2}}\right]\\ & =\frac{1}{8N+4}\left[1-{\left(-1\right)}^m\right]\cdot \sum _{l=0}^{N-1}Y[2l+1]\left[e^{j\frac{\pi \left(2l+1\right)m}{4N+2}}+e^{-j\frac{\pi \left(2l+1\right)m}{4N+2}}\right]\\ & =\frac{1}{4N+2}\left[1-{\left(-1\right)}^m\right]\cdot \sum _{l=0}^{N-1}Y[2l+1]\cos \left[\frac{\pi \left(2l+1\right)m}{4N+2}\right]\end{array}\text{\hspace{1em}(2-14)}$$

由此，定义 DCT-VIII 的计算公式如下，

$$\begin{array}{c}X[k]=DC{T}_8\left[x[n]\right]=4\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N+2}\right]\\ x[n]=IDC{T}_8\left[X[k]\right]=\frac{1}{2N+1}\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N+2}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-15)}$$

为了公式的一致性，将式（2-15）的系数平均分配到两边，则有

$$\begin{array}{c}X[k]=DC{T}_8\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N+2}\right]\\ x[n]=IDC{T}_8\left[X[k]\right]=\frac{2}{\sqrt{2N+1}}\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N+2}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-16)}$$

容易证明，类似于 DCT-II，式（2-16）所定义的离散余弦变换同样属于正交变换，在此不再赘述。

2.3 DCT-I

DCT-I 延拓的公式化表示如下，

$$\tilde{y}\left[m+k\left(2N-2\right)\right]=\tilde{x}\left[\left|m\right|\right],m=-N+1,-N+1,...,N-2.\text{\hspace{1em}(2-17)}$$

作为示例，图 2-1 所定义的有限长非对称实序列的 DCT-I 对称及周期延拓如图 2-7 所示，其对应的离散傅里叶变换序列如图 2-8 所示。

图 2-7 DCT-I 延拓 图 2-8 DCT-I 延拓序列的 DFT 序列

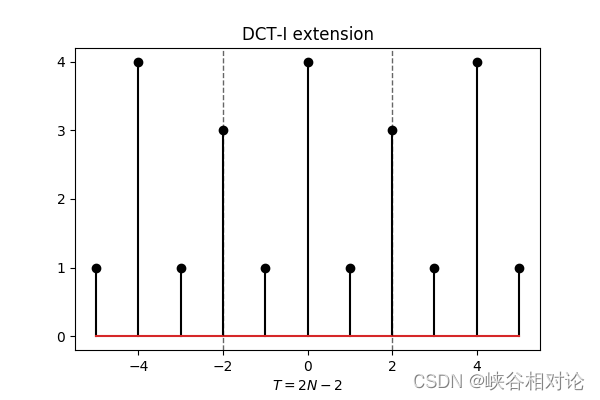
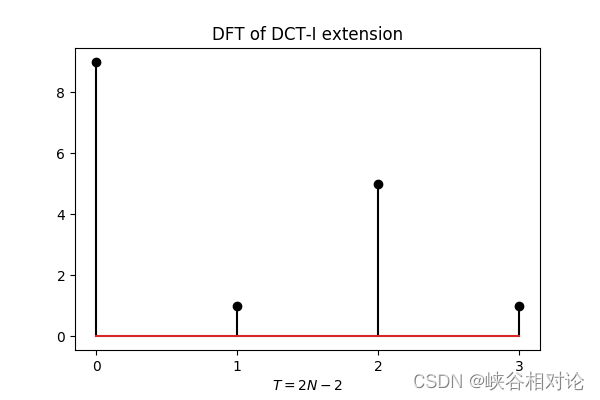
容易得到 DCT-I 对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DC{T}_1\left[x[n]\right]=\sqrt{\frac{2}{N-1}}{\gamma }_k{\gamma }_n\sum _{n=0}^{N-1}x[n]\cos \left(\frac{\pi kn}{N-1}\right)\\ x[n]=IDC{T}_1\left[X[k]\right]=\sqrt{\frac{2}{N-1}}{\gamma }_k{\gamma }_n\sum _{k=0}^{N-1}X[k]\cos \left(\frac{\pi kn}{N-1}\right)\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-18)}$$

其中

$${\gamma }_p=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& p=0orp=N-1\\ 1,& others\end{array}.$$

2.4 DCT-III

DCT-III 延拓的公式化表示如下，

$$\begin{array}{c}\tilde{y}[m+4kN]=\{\begin{array}{lc}\tilde{x}\left[\left|m\right|\right],& \left|m\right|⩽N-1\\ 0,& \left|m\right|=N\\ -\tilde{x}\left[2N-\left|m\right|\right],& \left|m\right|⩾N+1\end{array}\\ wherem=-2N,-2N+1,...,2N-1.\end{array}\text{\hspace{1em}(2-19)}$$

作为示例，图 2-1 所定义的有限长非对称实序列的 DCT-III 对称及周期延拓如图 2-9 所示，其对应的离散傅里叶变换序列如图 2-10 所示。

图 2-9 DCT-III 延拓 图 2-10 DCT-III 延拓序列的 DFT 序列

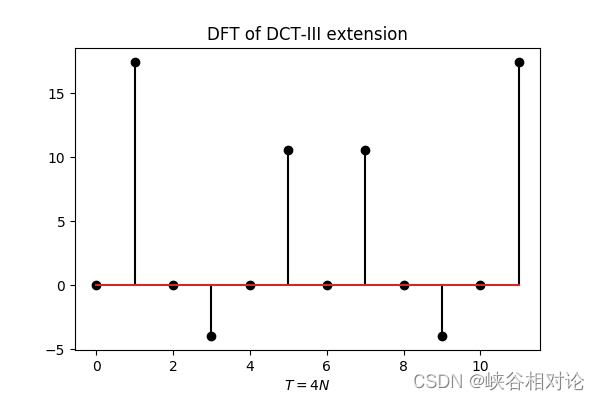
容易得到 DCT-III 对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DC{T}_3\left[x[n]\right]=\sqrt{\frac{2}{N}}{\epsilon }_n\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)n}{2N}\right]\\ x[n]=IDC{T}_3\left[X[k]\right]=\sqrt{\frac{2}{N}}{\epsilon }_n\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi \left(2k+1\right)n}{2N}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-20)}$$

其中

$${\epsilon }_n=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& n=0\\ 1,& n\ne 0\end{array}$$

2.5 DCT-IV

图 2-1 所示有限长非对称实序列 $x[n]$ 的 DCT-IV 对称及周期延拓如图 2-11(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 2-12(b) 所示。准确来说，延拓序列的公式化定义如式（2-21）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。

$$\begin{array}{c}\tilde{y}\left[m+8kN\right]=\{\begin{array}{lc}\tilde{x}\left[\frac{|m|-1}{2}\right],& \left|m\right|⩽2N-1\\ -\tilde{x}\left[\frac{4N-1-|m|}{2}\right],& \left|m\right|⩾2N\end{array}\\ wherem=-4N,-4N+1,...,4N-1.\end{array}\text{\hspace{1em}(2-21)}$$

图 2-11(b) 所示延拓序列的 DFT 序列如图 2-12 所示。

图 2-11 DCT-IV 延拓（a）及其插零上采样（b） 图 2-12 DCT-IV 延拓序列的 DFT 序列

容易可得 DCT-IV 对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DC{T}_4\left[x[n]\right]=\sqrt{\frac{2}{N}}\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N}\right]\\ x[n]=IDC{T}_4\left[X[k]\right]=\sqrt{\frac{2}{N}}\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N}\right]\\ wheren,k=0,1,...,N-1\end{array}\text{\hspace{1em}(2-22)}$$

2.6 DCT-V

DCT-V 延拓的公式化表示如下，

$$\tilde{y}\left[m+k\left(2N-1\right)\right]=\tilde{x}\left[\left|m\right|\right],m=-N+1,-N+2,...,N-1.\text{\hspace{1em}(2-23)}$$

作为示例，图 2-1 所定义的有限长非对称实序列的 DCT-V 对称及周期延拓如图 2-13 所示，其对应的离散傅里叶变换序列如图 2-14 所示。

图 2-13 DCT-V 延拓 图 2-14 DCT-V 延拓序列的 DFT 序列

容易得到DCT-V对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DC{T}_5\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\epsilon }_k{\epsilon }_n\sum _{n=0}^{N-1}x[n]\cos \left(\frac{2\pi kn}{2N-1}\right)\\ x[n]=IDC{T}_5\left[X[k]\right]=\frac{2}{\sqrt{2N-1}}{\epsilon }_k{\epsilon }_n\sum _{k=0}^{N-1}X[k]\cos \left(\frac{2\pi kn}{2N-1}\right)\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-24)}$$

其中

$${\epsilon }_p=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& p=0\\ 1,& p\ne 0\end{array}.$$

2.7 DCT-VI

图 2-1 所示有限长非对称实序列 $x[n]$ 的 DCT-VI 对称及周期延拓如图 2-15(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 2-15(b) 所示。准确来说，延拓序列的公式化定义如式（2-25）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。

$$\tilde{y}\left[m+k\left(4N-2\right)\right]=\tilde{x}\left[\frac{\left|m\right|-1}{2}\right],m=-2N+1,-2N+2,...,2N-2.\text{\hspace{1em}(2-25)}$$

图 2-15(b) 所示延拓序列的 DFT 序列如图 2-16 所示。

图 2-15 DCT-VI 延拓（a）及其插零上采样（b） 图 2-16 DCT-VI 延拓序列的 DFT 序列

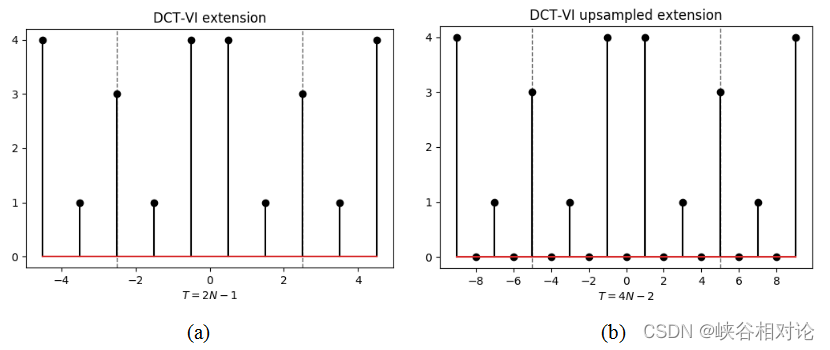
容易可得 DCT-VI 对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DC{T}_6\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\epsilon }_k{\eta }_n\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi k\left(2n+1\right)}{2N-1}\right]\\ x[n]=IDC{T}_6\left[X[k]\right]=\frac{2}{\sqrt{2N-1}}{\epsilon }_k{\eta }_n\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi k\left(2n+1\right)}{2N-1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-26)}$$

其中，

$${\epsilon }_k=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& k=0\\ 1,& k\ne 0\end{array},{\eta }_n=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& n=N-1\\ 1,& n\ne N-1\end{array}.$$

2.8 DCT-VII

DCT-VII 延拓的公式化表示如下，

$$\begin{array}{c}\tilde{y}\left[m+k\left(4N-2\right)\right]=\{\begin{array}{lc}\tilde{x}\left[\left|m\right|\right],& \left|m\right|⩽N-1\\ -\tilde{x}\left[2N-1-\left|m\right|\right],& \left|m\right|⩾N\end{array}\\ m=-2N+1,-2N+2,...,2N-2.\end{array}\text{\hspace{1em}(2-27)}$$

作为示例，图 2-1 所定义的有限长非对称实序列的 DCT-VII 对称及周期延拓如图 2-17 所示，其对应的离散傅里叶变换序列如图 2-18 所示。

图 2-17 DCT-VII 延拓 图 2-18 DCT-VII 延拓序列的 DFT 序列

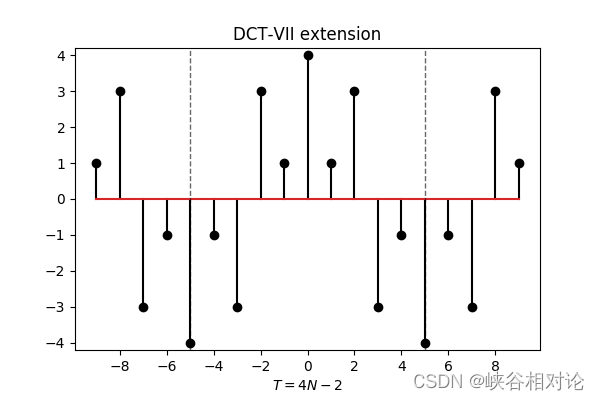
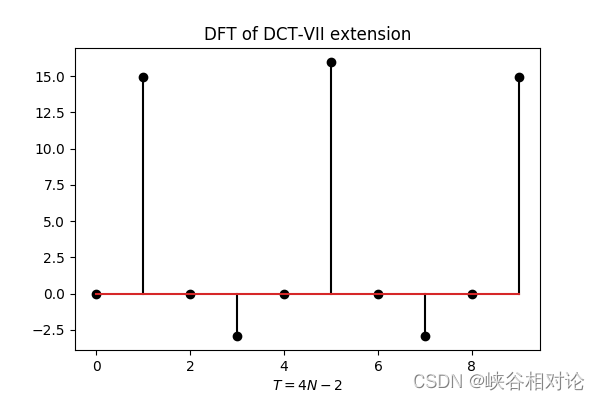
容易可得 DCT-VII 对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DC{T}_7\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\eta }_k{\epsilon }_n\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)n}{2N-1}\right]\\ x[n]=IDC{T}_7\left[X[k]\right]=\frac{2}{\sqrt{2N-1}}{\eta }_k{\epsilon }_n\sum _{k=0}^{N-1}X[k]\cos \left[\frac{\pi \left(2k+1\right)n}{2N-1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(2-28)}$$

其中，

$${\eta }_k=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& k=N-1\\ 1,& k\ne N-1\end{array},{\epsilon }_n=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& n=0\\ 1,& n\ne 0\end{array}.$$

附录

附录 A DCT 的 8 种延拓方式

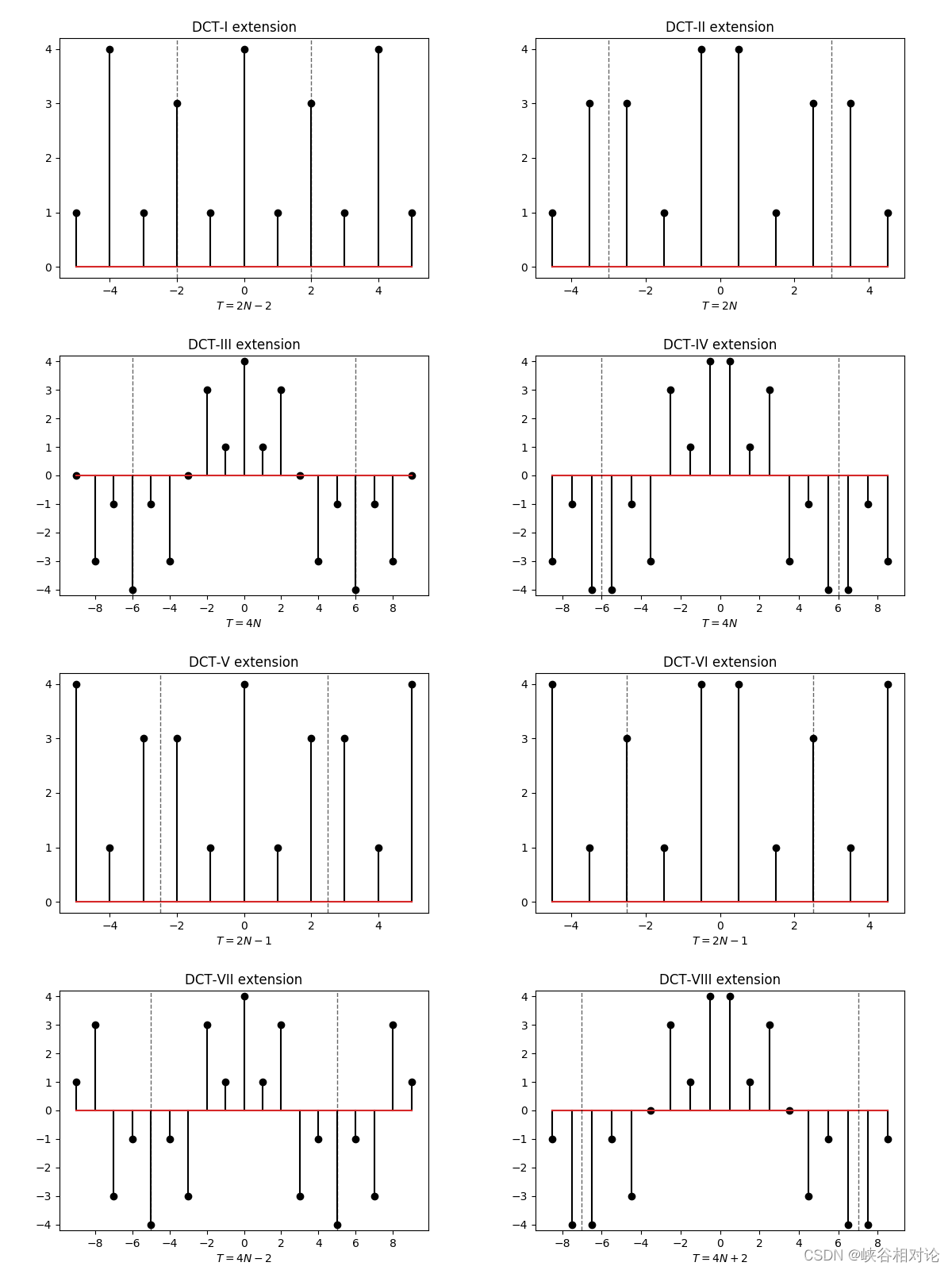
附录 B DCT 的 8 种变换公式

DCT-I

$$X[k]=DC{T}_1\left[x[n]\right]=\sqrt{\frac{2}{N-1}}{\gamma }_k{\gamma }_n\sum _{n=0}^{N-1}x[n]\cos \left(\frac{\pi kn}{N-1}\right).$$

DCT-II

$$X[k]=DC{T}_2\left[x[n]\right]=\sqrt{\frac{2}{N}}{\epsilon }_k\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi k\left(2n+1\right)}{2N}\right].$$

DCT-III

$$X[k]=DC{T}_3\left[x[n]\right]=\sqrt{\frac{2}{N}}{\epsilon }_n\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)n}{2N}\right].$$

DCT-IV

$$X[k]=DC{T}_4\left[x[n]\right]=\sqrt{\frac{2}{N}}\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N}\right].$$

DCT-V

$$X[k]=DC{T}_5\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\epsilon }_k{\epsilon }_n\sum _{n=0}^{N-1}x[n]\cos \left(\frac{2\pi kn}{2N-1}\right).$$

DCT-VI

$$X[k]=DC{T}_6\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\epsilon }_k{\eta }_n\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi k\left(2n+1\right)}{2N-1}\right].$$

DCT-VII

$$X[k]=DC{T}_7\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\eta }_k{\epsilon }_n\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)n}{2N-1}\right].$$

DCT-VIII

$$X[k]=DC{T}_8\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\cos \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N+2}\right].$$

$$\begin{array}{rl}{\epsilon }_p& =\{\begin{array}{cc}\frac{1}{\sqrt{2}},& p=0\\ 1,& p\ne 0\end{array},\\ {\eta }_p& =\{\begin{array}{cc}\frac{1}{\sqrt{2}},& p=N-1\\ 1,& p\ne N-1\end{array},\\ {\gamma }_p& =\{\begin{array}{cc}\frac{1}{\sqrt{2}},& p=0orp=N-1\\ 1,& others\end{array},\\ k,n,p& =0,1,...,N-1.\end{array}$$

附录 C DCT 的 8 种变换对应的基图像

DCT 基图像生成脚本

# -*- coding: utf-8 -*-
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt

def dct1_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k, :] = np.cos(np.pi * k * np.arange(N) / (N - 1))
    x[:,  0] /= np.sqrt(2)
    x[:, -1] /= np.sqrt(2)
    x[0,  :] /= np.sqrt(2)
    x[-1, :] /= np.sqrt(2)
    
    x *= np.sqrt(2. / (N - 1))
    return x

def dct2_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k, :] = np.cos(np.pi * k * (2 * np.arange(N) + 1) / (2 * N))
    x[0, :] /= np.sqrt(2)
    x *= np.sqrt(2. / N)
    return x
    
def dct3_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.cos(np.pi * (2 * k + 1) * np.arange(N) / (2 * N))
    x[:, 0] /= np.sqrt(2)
    x *= np.sqrt(2. / N)
    return x

def dct4_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.cos(np.pi * (2 * k + 1) * (2 * np.arange(N) + 1) / (4 * N))
    x *= np.sqrt(2. / N)
    return x

def dct5_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.cos(2 * np.pi * k * np.arange(N) / (2 * N - 1))
    x[:, 0] /= np.sqrt(2)
    x[0, :] /= np.sqrt(2)
    x *= np.sqrt(4. / (2 * N - 1))
    return x

def dct6_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.cos(np.pi * k * (2 * np.arange(N) + 1) / (2 * N - 1))
    x[:, -1] /= np.sqrt(2)
    x[0,  :] /= np.sqrt(2)
    x *= np.sqrt(4. / (2 * N - 1))
    return x

def dct7_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.cos(np.pi * (2 * k + 1) * np.arange(N) / (2 * N - 1))
    x[:,  0] /= np.sqrt(2)
    x[-1, :] /= np.sqrt(2)
    x *= np.sqrt(4. / (2 * N - 1))
    return x

def dct8_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.cos(np.pi * (2 * k + 1) * (2 * np.arange(N) + 1) / (4 * N + 2))
    x *= np.sqrt(4. / (2 * N + 1))
    return x

if __name__ == '__main__':
    path = 'dct_img/basis/'
    num = ['I', 'II', 'III', 'IV', 'V', 'VI', 'VII', 'VIII']
    
    for n in range(1, 9):
        kern = globals().get('dct{}_kern'.format(n))(8)
        '''
        把变换矩阵按行分块，记第k行的转置为ak，那么 h=[a1.T, a2.T, ..., a8.T]，
        用矩阵分块的知识得到 v.dot(h) 的每一个子块是 ai.dot(aj.T)，
        这样一次性就可以得到64个基图像拼起来的64x64的总图像了。
        '''
        h = kern.reshape([1, -1])
        v = h.T
        img = v.dot(h)
        
        plt.figure(figsize=(8, 8))
        plt.imshow(img, 'gray')
        plt.savefig(path+'/dct8x8_{}_all.png'.format(n), dpi='figure')
        
        imgs = []
        for i in range(8):
            for j in range(8):
                imgs.append(img[8*i:8*i+8, 8*j:8*j+8])
                #imgs.append(kern[[i], :].T.dot(kern[[j], :])) # 这种方法就是基图像一个一个地求

        imgs = np.stack(imgs)
        vmin, vmax = np.min(imgs), np.max(imgs)
        
        plt.figure(figsize=(32, 33))
        for i in range(8):
            for j in range(8):
                plt.subplot(8, 8, i*8+j+1)
                plt.imshow(imgs[i*8+j], 'gray', vmin=vmin, vmax=vmax)
                plt.axis('off')
                plt.tight_layout()
        plt.subplots_adjust(0.02, 0.02, 0.98, 0.95, 0.1, 0.1)
        plt.suptitle('DCT-'+num[n-1]+' basis', fontsize=48)
        plt.savefig(path+'/dct8x8_{}.png'.format(n), dpi=32)