理解DCT与DST【三】：离散正弦变换

本文主要是将先前的博客 离散傅里叶变换DFT、离散余弦变换DCT、离散正弦变换DST，原理与公式推导 从图片修改为 Markdown 脚本，方便读者浏览，同时增加了部分内容。但由于文章字符过多，无法全部放在一篇博客上，所以将之前的文章拆分为三部分，可通过以下链接查看其它部分。

• 理解DCT与DST【一】：离散傅里叶变换
• 理解DCT与DST【二】：离散余弦变换

3 离散正弦变换（Discrete Sine Transform, DST）

离散正弦变换类似于离散余弦变换，只是不同于离散余弦变换将有限长非对称实序列延拓为有限长对称实序列，离散正弦变换将有限长非对称实序列延拓为有限长反对称实序列。

由 1.5.5 节内容可知，对于一个有限长反对称实序列，其 DFT 序列乘上虚数单位 j 后同样是一个有限长反对称实序列。类似于有限长对称实序列，有限长反对称实序列的 DFT 的计算只需要用到序列的一半采样点数据，而且可以转化为只涉及正弦函数的实数运算，因此与离散余弦变换具有相似的计算复杂度。同样，离散正弦变换对应着非对称有限长实序列的反对称延拓序列的离散傅里叶变换的非冗余部分，不同的延拓方式对应着不同的延拓序列长度以及不同的离散傅里叶变换系数，因此也就对应着不同的离散正弦变换系数。根据 1.5.6 节的分析，离散傅里叶变换系数中的非冗余部分即独立分量的个数与原序列中的独立分量个数是一致的，因此离散正弦变换系数的个数也就对应着延拓序列中独立分量的个数。

数学上离散正弦变换总共定义了 8 种形式，且刚好与离散余弦变换的延拓方式相反，即将对称的地方改成反对称，将反对称的地方改成对称，从而对应着 8 种有限长非对称实序列的反对称延拓方式，分别用 DST-I ~ DST-VIII 来表示。在 H.266 视频编解码标准中，主要用到了 DST-VII，下面主要对其进行推导和分析，其他类型的 DST 只给出相应的延拓方式和对应的公式定义。

3.1 DST-VII

图 2-1 所示的有限长非对称实序列 $x[n]$ 的 DST-VII 反对称及周期延拓如图 3-1 所示。准确来说，延拓序列的公式化定义如式（3-1）所示，其中波浪线代表相应有限长序列的周期延拓。那么，有限长反对称实序列 $y[m]$ 的长度为 $4N+2$，而独立分量只有 $N$ 个，因此可以预见其 DFT 的独立分量也只有 $N$ 个。

$$\begin{array}{c}\tilde{y}\left[m+k\left(4N+2\right)\right]=\mathrm{sign}(m)\cdot \{\begin{array}{lc}\tilde{x}\left[\left|m\right|-1\right],& \left|m\right|⩽N\\ \tilde{x}\left[2N-\left|m\right|\right],& N+1⩽\left|m\right|⩽2N\\ 0,& \left|m\right|=2N+1\end{array}\\ wherem=-2N-1,-2N,...,2N.\end{array}\text{\hspace{1em}(3-1)}$$

图 3-1 DST-VII 延拓 图 3-2 DST-VII 延拓序列的 DFT 序列

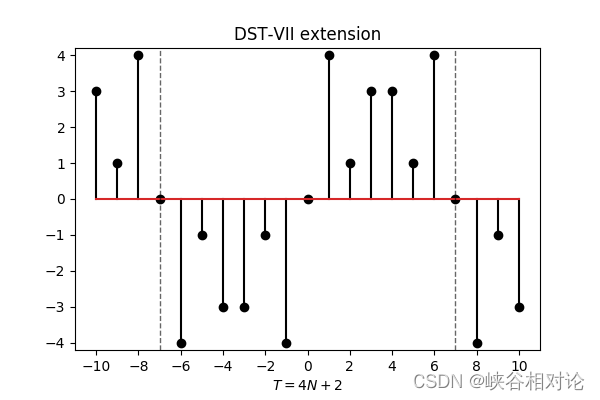
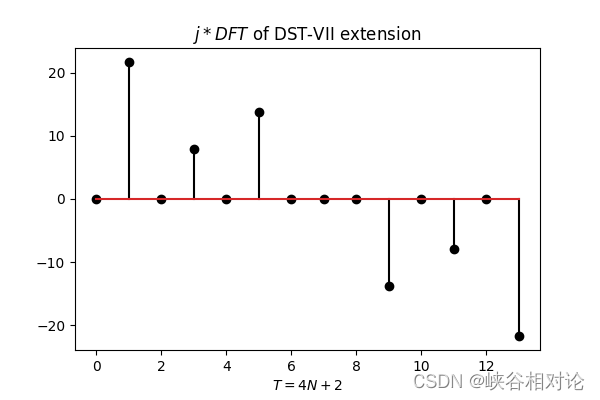
根据前面的内容，有

$$\begin{array}{rl}j\tilde{Y}[l]& =j\sum _{m=-2N-1}^{2N}\tilde{y}[m]e^{-j\frac{2\pi lm}{4N+2}}=j\sum _{m=1}^{2N-2}y[m]\left(e^{-j\frac{\pi lm}{2N+1}}-e^{j\frac{\pi lm}{2N+1}}\right)\\ & =2\sum _{m=1}^{2N}y[m]\sin \left(\frac{\pi lm}{2N+1}\right)\\ & =2\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi l\left(n+1\right)}{2N+1}\right]+2\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi l\left(2N+1-n-1\right)}{2N+1}\right]\\ & =2\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi l\left(n+1\right)}{2N+1}\right]+2\sum _{n=0}^{N-1}x[n]\sin \left[\pi l-\frac{\pi l\left(n+1\right)}{2N+1}\right]\\ & =2\cdot \left[1-{\left(-1\right)}^l\right]\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi l\left(n+1\right)}{2N+1}\right]\end{array}\text{\hspace{1em}(3-2)}$$

可得到以下性质，

$$\begin{array}{c}j\tilde{Y}[2l]=0,j\tilde{Y}[l]=-j\tilde{Y}[-l]\\ j\tilde{Y}[4N+2-l]=-j\tilde{Y}[l]\\ j\tilde{Y}[2N+1]=-j\tilde{Y}[4N+2-2N-1]=-j\tilde{Y}[2N+1]=0\end{array}\text{\hspace{1em}(3-3)}$$

所以，有限长反对称实序列 $y[m]$ 的 $4N+2$ 点 DFT 中的独立分量确实只有 $N$ 个。作为示例，图 3-1 中定义的延拓序列的 DFT 如图 3-2 所示。

根据以上性质，可以得到其逆变换为

$$\begin{array}{rl}y[m]& =\frac{1}{4N+2}\sum _{l=0}^{4N+1}Y[l]e^{j\frac{2\pi lm}{4N+2}}=\frac{-j}{4N+2}\sum _{l=0}^{4N+1}jY[l]e^{j\frac{2\pi lm}{4N+2}}\\ & =\frac{-j}{4N+2}\sum _{l=0}^{N-1}jY[2l+1]\left[e^{j\frac{2\pi \left(2l+1\right)m}{4N+2}}-e^{j\frac{2\pi \left(4N+2-2l-1\right)m}{4N+2}}\right]\\ & =\frac{-j}{4N+2}\sum _{l=0}^{N-1}jY[2l+1]\left[e^{j\frac{\pi \left(2l+1\right)m}{2N+1}}-e^{-j\frac{\pi \left(2l+1\right)m}{2N+1}}\right]\\ & =\frac{1}{2N+1}\sum _{l=0}^{N-1}jY[2l+1]\sin \left[\frac{\pi \left(2l+1\right)m}{2N+1}\right]\end{array}\text{\hspace{1em}(3-4)}$$

由此，定义 DST-VII 的计算公式如下，

$$\begin{array}{c}X[k]=DS{T}_7\left[x[n]\right]=jY[2k+1]=4\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N+1}\right]\\ x[n]=IDS{T}_7\left[X[k]\right]=y[n+1]=\frac{1}{2N+1}\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N+1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-5)}$$

为了公式的一致性，将式（3-5）的系数平均分配到两边，则有

$$\begin{array}{c}X[k]=DS{T}_7\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N+1}\right]\\ x[n]=IDS{T}_7\left[X[k]\right]=\frac{2}{\sqrt{2N+1}}\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N+1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-6)}$$

容易证明，类似于离散余弦变换，式（3-6）所定义的离散正弦变换同样属于正交变换，在此不再赘述。

3.2 DST-I

DST-I 延拓的公式化表示如下，

$$\begin{array}{c}\tilde{y}\left[m+k\left(2N+2\right)\right]=\mathrm{sign}\left(m\right)\cdot \{\begin{array}{lc}\tilde{x}\left[\left|m\right|-1\right],& \left|m\right|⩽N\\ 0,& m=-N-1\end{array}\\ wherem=-N-1,-N,...,N.\end{array}\text{\hspace{1em}(3-7)}$$

作为示例，图 2-1 所定义的有限长非对称实序列的 DST-I 反对称及周期延拓如图 3-3 所示，其对应的离散傅里叶变换序列如图 3-4 所示。

图 3-3 DST-I 延拓 图 3-4 DST-I 延拓序列的 DFT 序列

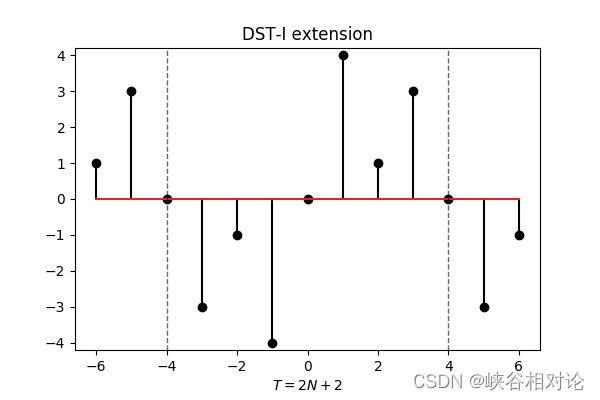
容易得到 DST-I 对应的离散正弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_1\left[x[n]\right]=\sqrt{\frac{2}{N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(k+1\right)\left(n+1\right)}{N+1}\right]\\ x[n]=IDS{T}_1\left[X[k]\right]=\sqrt{\frac{2}{N+1}}\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(k+1\right)\left(n+1\right)}{N+1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-8)}$$

3.3 DST-II

图 2-1 所示有限长非对称实序列 $x[n]$的 DST-II 反对称及周期延拓如图 3-5(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 3-5(b) 所示。准确来说，延拓序列的公式化定义如式（3-9）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。图 3-5(b) 所示延拓序列的 DFT 序列如图 3-6 所示。

$$\tilde{y}\left[m+4kN\right]=\mathrm{sign}\left(m\right)\cdot \tilde{x}\left[\frac{\left|m\right|-1}{2}\right],m=-2N,-2N+1,...,2N-1.\text{\hspace{1em}(3-9)}$$

图 3-5 DST-II 延拓（a）及其插零上采样（b） 图 3-6 DST-II 延拓序列的 DFT 序列

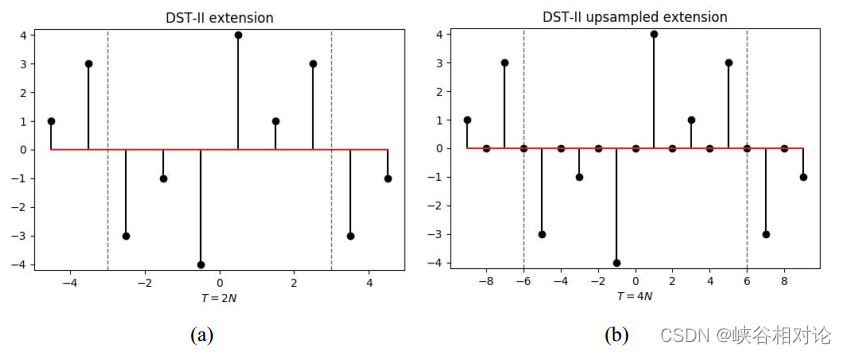
容易可得 DST-II 对应的离散正弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_2\left[x[n]\right]=\sqrt{\frac{2}{N}}{\eta }_k\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(k+1\right)\left(2n+1\right)}{2N}\right]\\ x[n]=IDS{T}_2\left[X[k]\right]=\sqrt{\frac{2}{N}}{\eta }_k\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(k+1\right)\left(2n+1\right)}{2N}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-10)}$$

其中

$${\eta }_k=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& k=N-1\\ 1,& k\ne N-1\end{array}.$$

3.4 DST-III

DST-III 延拓的公式化表示如下，

$$\begin{array}{c}\tilde{y}[m+4kN]=\mathrm{sign}\left(m\right)\cdot \{\begin{array}{lc}x\left[\left|m\right|-1\right],& \left|m\right|⩽N\\ x\left[2N-1-\left|m\right|\right],& N⩽\left|m\right|⩽2N-1\\ 0,& \left|m\right|=2N\end{array}\\ wherem=-2N,-2N+1,...,2N-1.\end{array}\text{\hspace{1em}(3-11)}$$

作为示例，图 2-1 所定义的有限长非对称实序列的 DST-III 反对称及周期延拓如图 3-7 所示，其对应的离散傅里叶变换序列如图 3-8 所示。

图 3-7 DST-III 延拓 图 3-8 DST-III 延拓序列的 DFT 序列

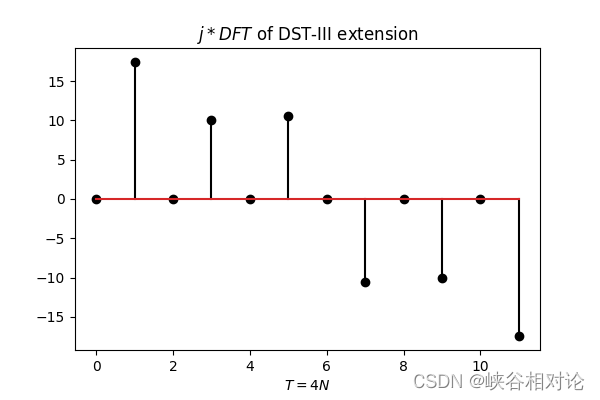
容易得到 DST-III 对应的离散正弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_3\left[x[n]\right]=\sqrt{\frac{2}{N}}{\eta }_n\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N}\right]\\ x[n]=IDS{T}_3\left[X[k]\right]=\sqrt{\frac{2}{N}}{\eta }_n\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-12)}$$

其中

$${\eta }_n=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& n=N-1\\ 1,& n\ne N-1\end{array}.$$

3.5 DST-IV

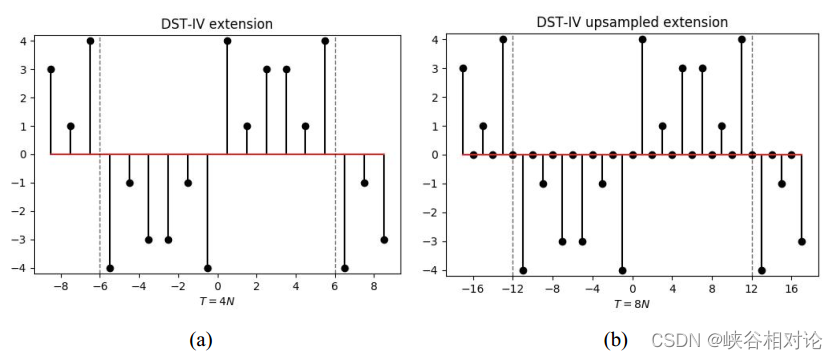
图 2-1 所示有限长非对称实序列 $x[n]$ 的 DST-IV 反对称及周期延拓如图 3-9(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 3-9(b) 所示。准确来说，延拓序列的公式化定义如式（3-13）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。图 3-9(b) 所示延拓序列的 DFT 序列如图 3-10 所示。

$$\begin{array}{c}\tilde{y}\left[m+8kN\right]=\mathrm{sign}\left(m\right)\cdot \{\begin{array}{lc}\tilde{x}\left[\frac{|m|-1}{2}\right],& \left|m\right|⩽2N-1\\ \tilde{x}\left[\frac{4N-1-|m|}{2}\right],& \left|m\right|⩾2N\end{array}\\ wherem=-4N,-4N+1,...,4N-1.\end{array}\text{\hspace{1em}(3-13)}$$

图 3-9 DST-IV 延拓（a）及其插零上采样（b） 图 3-10 DST-IV 延拓序列的 DFT 序列

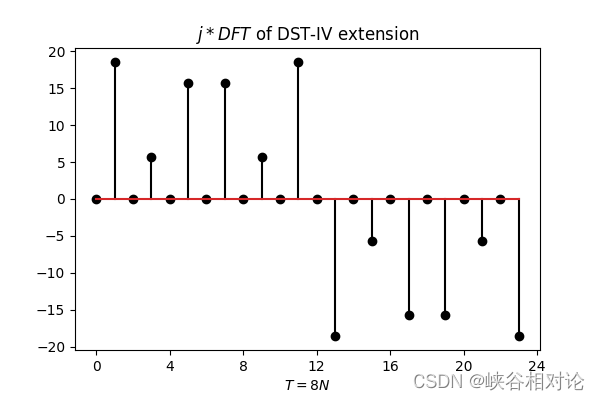
容易可得 DST-IV 对应的离散正弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_4\left[x[n]\right]=\sqrt{\frac{2}{N}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N}\right]\\ x[n]=IDS{T}_4\left[X[k]\right]=\sqrt{\frac{2}{N}}\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-14)}$$

3.6 DST-V

DST-V 延拓的公式化表示如下，

$$\tilde{y}\left[m+k\left(2N+1\right)\right]=\mathrm{sign}\left(m\right)\cdot \tilde{x}\left[\left|m\right|-1\right],m=-N,-N+1,...,N.\text{\hspace{1em}(3-15)}$$

作为示例，图 2-1 定义的有限长非对称实序列的 DST-V 反对称及周期延拓如图 3-11 所示，其对应的离散傅里叶变换序列如图 3-12 所示。

图 3-11 DST-V 延拓 图 3-12 DST-V 延拓序列的 DFT 序列

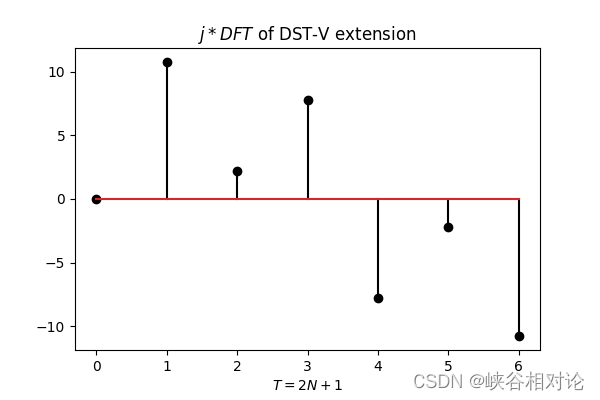
容易得到 DST-V 对应的离散正弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_5\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{2\pi \left(k+1\right)\left(n+1\right)}{2N+1}\right]\\ x[n]=IDS{T}_5\left[X[k]\right]=\frac{2}{\sqrt{2N+1}}\sum _{k=0}^{N-1}X[k]\sin \left[\frac{2\pi \left(k+1\right)\left(n+1\right)}{2N+1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-16)}$$

3.7 DST-VI

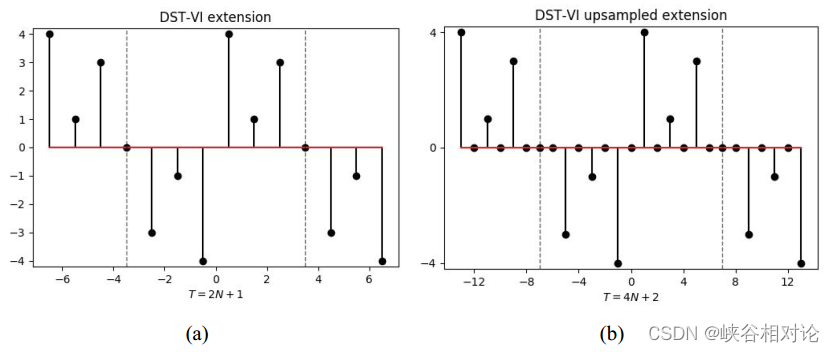
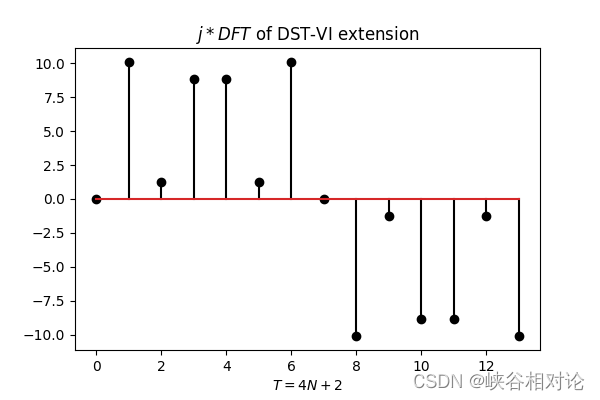
图 2-1 的有限长非对称实序列 $x[n]$ 的 DST-VI 反对称及周期延拓如图 3-13(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，因此需要对该序列进行 2 倍插零上采样，得到离散序列如图 3-13(b) 所示。准确来说，延拓序列的公式化定义如式（3-17）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。图 3-13(b) 所示延拓序列的 DFT 序列如图 3-14 所示。

$$\begin{array}{c}\tilde{y}\left[m+k\left(4N+2\right)\right]=\mathrm{sign}\left(m\right)\cdot \{\begin{array}{lc}\tilde{x}\left[\frac{|m|-1}{2}\right],& \left|m\right|⩽2N\\ 0,& \left|m\right|=2N+1\end{array}\\ wherem=-2N-1,-2N,...,2N.\end{array}\text{\hspace{1em}(3-17)}$$

容易可得 DST-VI 对应的离散余弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_6\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(k+1\right)\left(2n+1\right)}{2N+1}\right]\\ x[n]=IDS{T}_6\left[X[k]\right]=\frac{2}{\sqrt{2N+1}}\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(k+1\right)\left(2n+1\right)}{2N+1}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-18)}$$

图 3-13 DST-VI 延拓（a）及其插零上采样（b） 图 3-14 DST-VI 延拓序列的 DFT 序列

3.8 DST-VIII

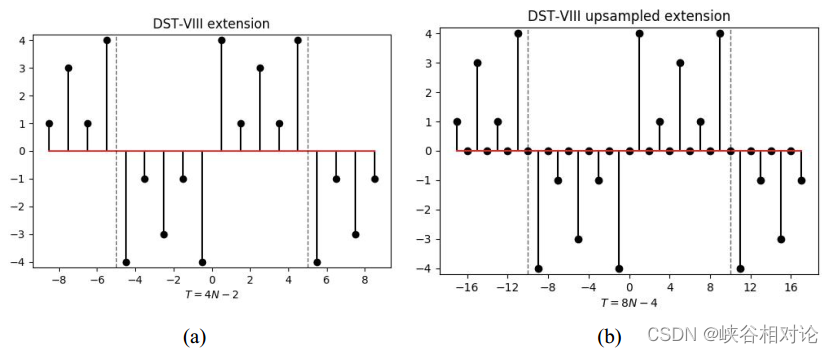
图 2-1 的有限长非对称实序列 $x[n]$ 的 DST-VIII 反对称及周期延拓如图 3-15(a) 所示。由于序列右移了 1/2，所有采样点都处于非整数索引位置，因此需要对该序列进行 2 倍的插零上采样，得到离散序列如图 3-15(b) 所示。准确来说，延拓序列的公式化定义如式（3-19）所示，其中波浪线代表相应有限长序列的周期延拓，非整数索引位置默认为 0。图 3-15(b) 所示延拓序列的 DFT 序列如图 3-16 所示。

$$\begin{array}{c}\tilde{y}\left[m+k\left(8N-4\right)\right]=\mathrm{sign}\left(m\right)\cdot \{\begin{array}{lc}\tilde{x}\left[\frac{|m|-1}{2}\right],& \left|m\right|⩽2N-1\\ \tilde{x}\left[\frac{4N-3-|m|}{2}\right],& \left|m\right|⩾2N\end{array}\\ wherem=-4N+2,-4N+3,...,4N-3.\end{array}\text{\hspace{1em}(3-19)}$$

图 3-15 DST-VIII 延拓（a）及其插零上采样（b） 图 3-16 DST-VIII 延拓序列的 DFT 序列

容易可得 DST-VIII 对应的离散正弦变换公式如下，

$$\begin{array}{c}X[k]=DS{T}_8\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\eta }_k{\eta }_n\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N-2}\right]\\ x[n]=IDS{T}_8\left[X[k]\right]=\frac{2}{\sqrt{2N-1}}{\eta }_k{\eta }_n\sum _{k=0}^{N-1}X[k]\sin \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N-2}\right]\\ wheren,k=0,1,...,N-1.\end{array}\text{\hspace{1em}(3-20)}$$

其中，

$${\eta }_p=\{\begin{array}{lc}\frac{1}{\sqrt{2}},& p=N-1\\ 1,& p\ne N-1\end{array}.$$

附录 A DST的 8 种延拓方式

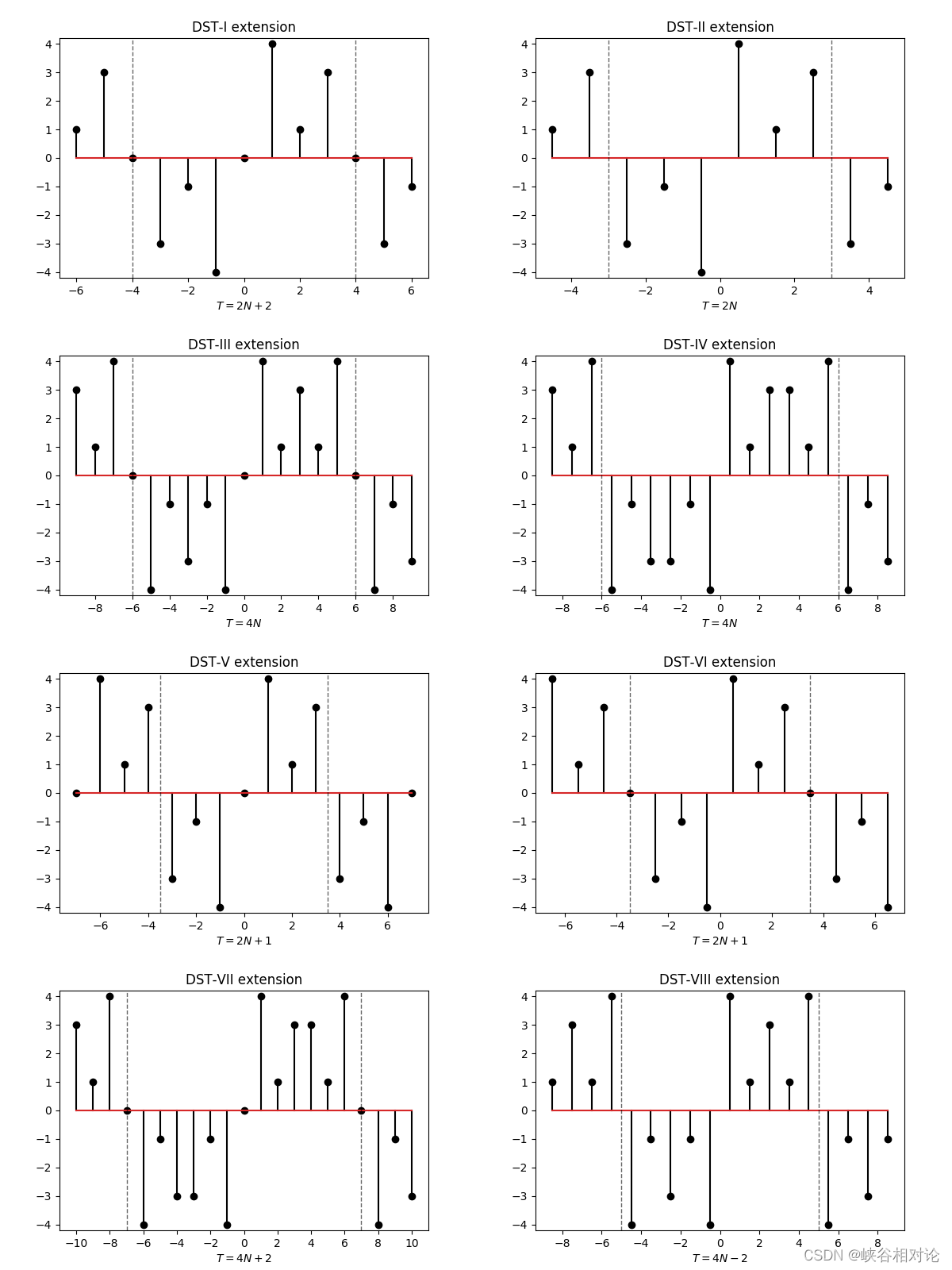
附录 B DST 的 8 种变换公式

DST-I

$$X[k]=DS{T}_1\left[x[n]\right]=\sqrt{\frac{2}{N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(k+1\right)\left(n+1\right)}{N+1}\right].$$

DST-II

$$X[k]=DS{T}_2\left[x[n]\right]=\sqrt{\frac{2}{N}}{\eta }_k\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(k+1\right)\left(2n+1\right)}{2N}\right].$$

DST-III

$$X[k]=DS{T}_3\left[x[n]\right]=\sqrt{\frac{2}{N}}{\eta }_n\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N}\right].$$

DST-IV

$$X[k]=DS{T}_4\left[x[n]\right]=\sqrt{\frac{2}{N}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N}\right].$$

DST-V

$$X[k]=DS{T}_5\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{2\pi \left(k+1\right)\left(n+1\right)}{2N+1}\right].$$
DST-VI

$$X[k]=DS{T}_6\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(k+1\right)\left(2n+1\right)}{2N+1}\right].$$

DST-VII

$$X[k]=DS{T}_7\left[x[n]\right]=\frac{2}{\sqrt{2N+1}}\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(n+1\right)}{2N+1}\right].$$

DST-VIII

$$X[k]=DS{T}_8\left[x[n]\right]=\frac{2}{\sqrt{2N-1}}{\eta }_k{\eta }_n\sum _{n=0}^{N-1}x[n]\sin \left[\frac{\pi \left(2k+1\right)\left(2n+1\right)}{4N-2}\right].$$

$${\eta }_p=\{\begin{array}{cc}\frac{1}{\sqrt{2}},& p=N-1\\ 1,& p\ne N-1\end{array},k,n,p=0,1,...,N-1.$$

附录 C DST 的 8 种变换对应的基图像

DST 基图像生成脚本

# -*- coding: utf-8 -*-
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt

def dst1_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k, :] = np.sin(np.pi * (k + 1) * (np.arange(N) + 1) / (N + 1))
    x *= np.sqrt(2. / (N + 1))
    return x

def dst2_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k, :] = np.sin(np.pi * (k + 1) * (2 * np.arange(N) + 1) / (2 * N))
    x[-1, :] /= np.sqrt(2)
    x *= np.sqrt(2. / N)
    return x
    
def dst3_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.sin(np.pi * (2 * k + 1) * (np.arange(N) + 1) / (2 * N))
    x[:, -1] /= np.sqrt(2)
    x *= np.sqrt(2. / N)
    return x

def dst4_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.sin(np.pi * (2 * k + 1) * (2 * np.arange(N) + 1) / (4 * N))
    x *= np.sqrt(2. / N)
    return x

def dst5_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.sin(2 * np.pi * (k + 1) * (np.arange(N) + 1) / (2 * N + 1))
    x *= np.sqrt(4. / (2 * N + 1))
    return x

def dst6_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.sin(np.pi * (k + 1) * (2 * np.arange(N) + 1) / (2 * N + 1))
    x *= np.sqrt(4. / (2 * N + 1))
    return x

def dst7_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.sin(np.pi * (2 * k + 1) * (np.arange(N) + 1) / (2 * N + 1))
    x *= np.sqrt(4. / (2 * N + 1))
    return x

def dst8_kern(N):
    x = np.zeros([N, N])
    for k in range(N):
        x[k] = np.sin(np.pi * (2 * k + 1) * (2 * np.arange(N) + 1) / (4 * N - 2))
    x[:, -1] /= np.sqrt(2)
    x[-1, :] /= np.sqrt(2)
    x *= np.sqrt(4. / (2 * N - 1))
    return x

if __name__ == '__main__':
    path = 'dst_img/basis/'
    num = ['I', 'II', 'III', 'IV', 'V', 'VI', 'VII', 'VIII']
    
    for n in range(1, 9):
        kern = globals().get('dst{}_kern'.format(n))(8)
        '''
        把变换矩阵按行分块，记第k行的转置为ak，那么 h=[a1.T, a2.T, ..., a8.T]，
        用矩阵分块的知识得到 v.dot(h) 的每一个子块是 ai.dot(aj.T)，
        这样一次性就可以得到64个基图像拼起来的64x64的总图像了。
        '''
        h = kern.reshape([1, -1])
        v = h.T
        img = v.dot(h)
        
        plt.figure(figsize=(8, 8))
        plt.imshow(img, 'gray')
        plt.savefig(path+'/dst8x8_{}_all.png'.format(n), dpi='figure')
        
        imgs = []
        for i in range(8):
            for j in range(8):
                imgs.append(img[8*i:8*i+8, 8*j:8*j+8])
                #imgs.append(kern[[i], :].T.dot(kern[[j], :])) # 这种方法就是基图像一个一个地求

        imgs = np.stack(imgs)
        vmin, vmax = np.min(imgs), np.max(imgs)
        
        plt.figure(figsize=(32, 33))
        for i in range(8):
            for j in range(8):
                plt.subplot(8, 8, i*8+j+1)
                plt.imshow(imgs[i*8+j], 'gray', vmin=vmin, vmax=vmax)
                plt.axis('off')
                plt.tight_layout()
        plt.subplots_adjust(0.02, 0.02, 0.98, 0.95, 0.1, 0.1)
        plt.suptitle('DST-'+num[n-1]+' basis', fontsize=48)
        plt.savefig(path+'/dst8x8_{}.png'.format(n), dpi=32)