机器学习需要认识的概率

概率基本概念

$P(E)=\frac{n(E)}{n(S)}$

n(E)：特定事件集合

n(S)：样本空间

概率的范围如下所示：

$0\leq P\leq 1$

P=0，表示事件不存在或不可能发生，如果P=1，表示事件一定会发生。

使用随机数函数randint(min,max),min=1,max=6,然后执行1000次，最后列出产生5的次数与概率。

import random           # 导入模块random

min = 1
max = 6
target = 5
n = 10000
counter = 0
for i in range(n):
    if target == random.randint(min, max):
        counter += 1
print('经过 {} 次, 得到 {} 次 {}'.format(n, counter, target))
P = counter / n
print('机率 P = {}'.format(P))

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
经过 10000 次, 得到 1638 次 5
机率 P = 0.1638

[Done] exited with code=0 in 0.367 seconds

使用随机数产生10000次1、2、3、4、5、6的随机数，最后将结果建立直方图，同时列出每个点数的产生次数。

import matplotlib.pyplot as plt
from random import randint

min = 1
max = 6                                         # 骰子有几面
times = 10000                                   # 掷骰子次数

dice = [0] * 7                                  # 建立掷骰子的列表
for i in range(times):
    data = randint(min, max)
    dice[data] += 1
    
del dice[0]                                     # 删除索引0数据
    
for i, c in enumerate(dice, 1):
    print('{} = {} 次'.format(i, c))
    
x = [i for i in range(1, max+1)]                # 直方图x轴坐标
width = 0.35                                    # 直方图宽度
plt.bar(x, dice, width, color='g')              # 绘制直方图
plt.ylabel('Frequency')
plt.title('Test 10000 times')
plt.show()

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
1 = 1659 次
2 = 1688 次
3 = 1672 次
4 = 1679 次
5 = 1674 次
6 = 1628 次

[Done] exited with code=0 in 12.478 seconds

数学概率与统计概率

统计概率使用下列公式表达：

$P(E)=\frac{E}{S}$

事件概率名称

事件：

在样本中每个子集合，称事件。

必然事件：

在概率事件中一定会发生的事件称必然事件。

$P(\Omega )=1$

掷骰子的样本空间是{1，2，3，4，5，6}，所掷的骰子点数一定是在1~6，所有这就是必然事件。

不可能事件：

在概率事件中一定不会发生的事件称不可能事件，也就是不可能发生的样本空间内的事件。不可能事件可以用 $\varnothing$ 表示，所以得到下列结果。

$P(\varnothing )=0$ #所有不在样本空间内的事件，事件发生概率是0

掷骰子的样本空间是{1，2，3，4，5，6}，所掷的骰子一定不会是0，所以这就是不可能事件。

余事件：

在掷骰子事件中，出现5的概率是 $\frac{1}{6}$ ，所谓余事件就是出现非5的其他事件，此时得到出现非5的概率是 $\frac{5}{6}$ 。

互斥事件：

如果事件A与事件B产生下列情况，称A与B为互斥事件。

$A\cap B=\varnothing$

事件概率规则

不发生概率

其实这和余事件概念相同，假设事件A的发生概率是P(A)，则事件A的不发生概率是：

$P(\bar{A})=1-P(A)$

相率相加

两个事件不会同时发生，或者说这两件事是独立事件。可将概率相加称和事件。

$P=P(A)+P(B)$

掷骰子时，如果要计算产生偶数{2,4,6}的概率，可以使用下列公式：

$P=P(2)+P(4)+P(6)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{3}{6}=\frac{1}{2}$

概率相乘

掷骰子时，连续出现5的概率是多少？

使用概率相乘就可以算出连续2次出现5的概率，参考下列公式：

$P=\frac{1}{6}*\frac{1}{6}=\frac{1}{36}$

常见的陷阱

省略

抽奖的概率：加法与乘法综合应用

公司要举办员工欧州旅游抽奖，有7支签，其中2支签是公司补助全额旅费。

第1位：中奖 $\frac{2}{7}$ 无 $\frac{5}{7}$

第2位：中奖 $\frac{1}{6}$ 无 $\frac{5}{6}$ 中奖 $\frac{2}{6}$ 无 $\frac{4}{6}$

如果第1位员工中奖，第2位员工也中奖，概率计算方式是使用概率相乘：

$\frac{2}{7}*\frac{1}{6}=\frac{2}{42}$

如果第1位员工没中奖，第2位员工中奖，概率计算方式也是使用概率相乘：

$\frac{5}{7}*\frac{2}{6}=\frac{10}{42}$

由于上述事件不会同时发生，所以执行加法运算：

$\frac{2}{42}+\frac{10}{42}=\frac{12}{42}=\frac{2}{7}$

Python内有fractions模块，可以执行分数的运算。

计算第2位员工的中奖概率。

from fractions import Fraction

x = Fraction(2, 7) * Fraction(1, 6)
y = Fraction(5, 7) * Fraction(2, 6)
p = x + y
print('第 1 位抽签的中奖机率 {}'.format(Fraction(2, 7)))
print('第 2 位抽签的中奖机率 {}'.format(p))

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
第 1 位抽签的中奖机率 2/7
第 2 位抽签的中奖机率 2/7

[Done] exited with code=0 in 0.239 seconds

余事件与乘法的综合应用

连掷3次骰子，请问至少出现一次点数5的概率是多少？

（1）掷骰子不出现5的概率是 $\frac{5}{6}$ 。

（2）连掷3次骰子不出现5的概率是 $\frac{5}{6}*\frac{5}{6}*\frac{5}{6}=\frac{125}{216}=0.5787$ 。

（3）连掷3次至少出现1次5的概率计算方式是采用余事件，概念如下：

P（至少出现1次5的概率）=1-P（不出现5的概率）

p=1-0.5787=0.4213

所以可以得到连掷3次骰子，至少出现一次点数5的概率是0.4213。

计算连掷3次骰子，至少出现一次点数5的概率。

from fractions import Fraction

x = Fraction(5, 6)
p = 1 - (x**3)
print('连掷骰子不出现 5 的机率 {}'.format(p))
print('连掷骰子不出现 5 的机率 {}'.format(float(p)))

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
连掷骰子不出现 5 的机率 91/216
连掷骰子不出现 5 的机率 0.4212962962962963

[Done] exited with code=0 in 0.723 seconds

条件概率

P（A事件发生的概率）=P（A）

P（B事件发生的概率）=P（B）

P（A事件与B事件同时出现的概率）=P(A $\cap$ B)

P（已知A事件下，B事件出现的概率）=P(B|A)

P（已知B事件下，A事件出现的概率）=P(A|B)

当掷一颗六面骰子，样本空间是{1,2,3,4,5,6}，假设情况如下：

A={5,6} #点数大于4的事件

B={1,3,5} #点数是奇数的事件

P(A|B)是在发生骰子点数是奇数时，出现点数大于4的概率；

P(B|A)是骰子点数大于4时，出现奇数的概率。

$P(A|B)=\frac{P(A\cap B))}{P(B)}=\frac{P(5)}{P(B)}=\frac{\frac{1}{6}}{\frac{3}{6}}=\frac{1}{3}$

$P(B|A)=\frac{P(B\cap A))}{P(A)}=\frac{P(5)}{P(A)}=\frac{\frac{1}{6}}{\frac{2}{6}}=\frac{1}{2}$

贝氏定理

基本概念

在条件概率的应用中有一个重要的定义称贝叶斯定理（Bayes' theorem）,这是描述在已知条件下，某一事件发生的概率。基本概念是已知事件A的条件下发生事件B的概率，与已知事件B的条件下发生事件A的概率不一样，但是两者有关联，贝叶斯定理就是描述这个关系。 $P(A|B)=\frac{P(A\cap B))}{P(B)}$

$P(B|A)=\frac{P(B\cap A))}{P(A)}$

$P(A|B)P(B)=P(A\cap B)=P(B|A)P(A)$

$P(A|B)P(B)=P(B|A)P(A)$

$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

用实例验证贝叶斯定理

$P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{\frac{1}{2}*\frac{2}{6}}{\frac{3}{6}}=\frac{1}{3}$

$P(B|A)=\frac{P(A|B)P(B)}{P(A)}=\frac{\frac{1}{3}*\frac{3}{6}}{\frac{2}{6}}=\frac{1}{2}$

贝叶斯定理的运用：COVID-19的全民普筛准确性预估

省略

使用贝叶斯定理筛选垃圾电子邮件

省略

蒙地卡罗模拟

用蒙地卡罗模拟随机数计算Pi值，这个程序会产生100万个随机点。

import random

trials = 1000000
Hits = 0
for i in range(trials):
    x = random.random() * 2 - 1     # x轴坐标
    y = random.random() * 2 - 1     # y轴坐标
    if x * x + y * y <= 1:          # 判断是否在圆内
        Hits += 1
PI = 4 * Hits / trials

print("PI = ", PI)

运行结果如下：

[Running] python -u "c:\Users\a-xiaobodou\OneDrive - Microsoft\Projects\tempCodeRunnerFile.py"
PI =  3.142084

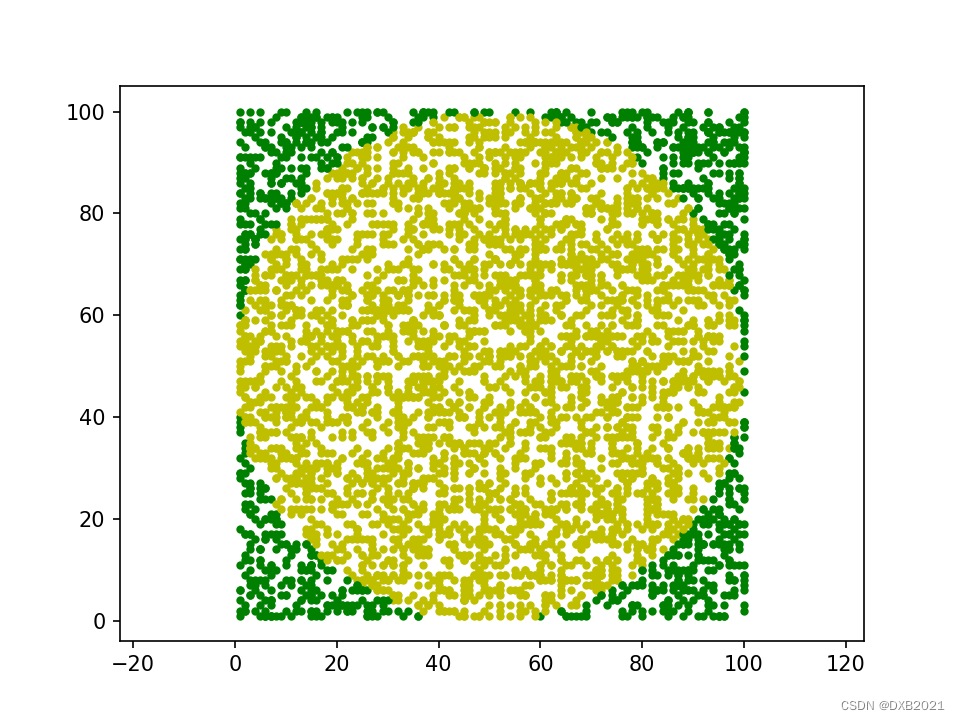
[Done] exited with code=0 in 1.489 seconds

使用matplotlib模块，如果点落在圆内绘黄色点，如果落在圆外绘绿色点，直接使用randint()方法产生随机数，同时将所绘制的图落在x=0~100，y=0~100的范围内。由于绘图会需要比较多时间，所以测试5000次。

import random
import math
import matplotlib.pyplot as plt

trials = 5000
Hits = 0
radius = 50
for i in range(trials):
    x = random.randint(1, 100)                      # x轴坐标
    y = random.randint(1, 100)                      # y轴坐标
    if math.sqrt((x-50)**2 + (y-50)**2) < radius:   # 在圆内
        plt.scatter(x, y, marker='.', c='y')
        Hits += 1
    else:
        plt.scatter(x, y, marker='.', c='g')    
plt.axis('equal')
plt.show()

运行结果如下：