文章目录
- 1:master公式的用法
- 2:实际例子
-
- 2-1:用分治法解决一个规模为N的问题。若每步将问题分成规模均为N/3的8个子问题,且治而得到解的步骤耗时O(N^2logN),则整个算法的时间复杂度为
- 2-2:用分治法解决一个规模为N的问题。下列哪种方法是最慢的?
- 2-3:给定程序时间复杂度的递推公式:T(1)=1,T(N)=2T(N/2)+ N。则对该程序时间复杂度最接近的描述是:
- 2-4:用分治法解决一个规模为N的问题时,若每步将问题划分为4个规模为N/2的子问题,并且用O(N^2logN)的时间执行治。则下列哪项最接近于整体时间复杂度?
- 2-5:给定两个n × n的矩阵A和B。考虑下列计算矩阵乘积C= A·B的分治法。将每个矩阵划分为如下四个 n 2 × n 2 \frac{n}{2}×\frac{n}{2} 2n×2n的子矩阵:
- 2-6:假如需要计算以下6个矩阵的依次连乘:
1:master公式的用法
T(N) = a * T(N / b) + f(N) (f(N) 为多项式 Nd …)
(1)log(b, a) > d ==> 时间复杂度为O(Nlog(b,a))
(2)log(b, a) = d ==> 时间复杂度为O(Nd * log(N))
(3)log(b, a) < d ==> 时间复杂度为f(N)
2:实际例子
2-1:用分治法解决一个规模为N的问题。若每步将问题分成规模均为N/3的8个子问题,且治而得到解的步骤耗时O(N^2logN),则整个算法的时间复杂度为
解析:T(N) = 8(N / 3) + (N2)
可得:a = 8, b = 3, d = 2
log(3, 8) < 2 ==> 时间复杂度为O(N2logN)
A. O(N2logN)
B. O(N2log2N)
C.O(N3logN)
D.O(Nlog8/log3)
2-2:用分治法解决一个规模为N的问题。下列哪种方法是最慢的?
A.每步将问题分成规模均为N/3的2个子问题,且治的步骤耗时O(N)
解析:T(N) = 2(N / 3) + N
可得:a = 2, b = 3, d = 1
log(3, 2) < 1 ==> 时间复杂度为O(N)
B.每步将问题分成规模均为N/3的2个子问题,且治的步骤耗时O(NlogN)
解析:T(N) = 2(N / 3) + N
可得:a = 2, b = 3, d = 1
log(3, 2) < 1 ==> 时间复杂度为O(NlogN)
C.每步将问题分成规模均为N/2的3个子问题,且治的步骤耗时O(N)
解析:T(N) = 3(N / 2) + N
可得:a = 3, b = 2, d = 1
log(2, 3) > 1 ==> 时间复杂度为O(Nlog(2,3))
D.每步将问题分成规模均为N/3的3个子问题,且治的步骤耗时O(NlogN)
解析:T(N) = 3(N / 3) + N
可得:a = 3, b = 3, d = 1
log(3, 3) == 1 ==> 时间复杂度为O(NlogN)
2-3:给定程序时间复杂度的递推公式:T(1)=1,T(N)=2T(N/2)+ N。则对该程序时间复杂度最接近的描述是:
解析:T(N) = 2(N / 2) + N
可得:a = 2, b = 2, d = 1
log(2, 2) == 1 ==> 时间复杂度为O(NlogN)
A. O(logN)
B. O(N)
C. O(NlogN)
D. O(N2)
2-4:用分治法解决一个规模为N的问题时,若每步将问题划分为4个规模为N/2的子问题,并且用O(N^2logN)的时间执行治。则下列哪项最接近于整体时间复杂度?
解析:T(N) = 4(N / 2) + N2
可得:a = 4, b = 2, d = 2
log(2, 4) == 2 ==> 时间复杂度为O(N2) * logN * logN == O(N2 log2N)
A. O(N2logN)
B. O(N2)
C. O(N3logN)
D. O(N2log2N)
2-5:给定两个n × n的矩阵A和B。考虑下列计算矩阵乘积C= A·B的分治法。将每个矩阵划分为如下四个 n 2 × n 2 \frac{n}{2}×\frac{n}{2} 2n×2n的子矩阵:
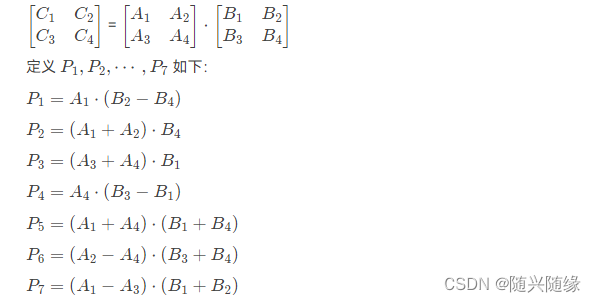
这里所有的矩阵乘法都是递归完成的。矩阵 C 的每一块都可以利用 P1,P2 ,⋯,P7通过加减运算得到。
以下哪一项最接近实际的算法时间复杂度?
解析:此问题可以看成7个(N / 2)的子问题
即:a = 2, b = 7
所以为:O ( n l o g 2 7 n^{log_{2}7} nlog27)
A.O( n 2 l o g 2 n n^{2}log_{2}n n2log2n)
B. O(ne)
C.O ( n l o g 2 7 n^{log_{2}7} nlog27)
D. o( n 3 n^{3} n3)
2-6:假如需要计算以下6个矩阵的依次连乘:

求解最优乘法次数的递推计算得到如下递推矩阵m[i][j]:
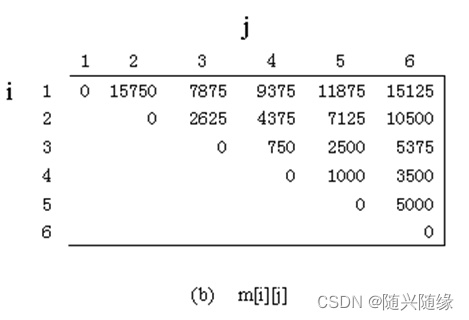
那么,A2到A5的子问题最少的乘法次数是多少次?
解析:根据动态规划算法的性质,最次得到的结果都为当前最优解,所以直接查表即可
A. 5000
B.2500
C.4375
D.7125
持续更新中…