1 神经网络介绍
定义
- 人工神经网络(Artificial Neural Networks ),简称神经网络
- 人脑神经系统启发、早期神经科学家构造了一种模仿人脑神经系统的数学模型
- 机器学习领域的神经网络:由很多人工神经元构成的网络结构模型、人工神经元之间的连接强度是科学系的参数----学习
神经网络组成结构
- 神经元:人工神经网络中最小也是最重要的单元
- 一个生物神经元具有多个树突和一个轴突。树突用来接收信息,轴突用来发送信息。当神经元所获得的输入信号积累超过某个阈值时,处于兴奋状态,产生电脉冲。轴突尾端有许多末梢可以与其他神经元的树突产生连接,并将电脉冲信号传递给其他神经元
- 与生物神经系统类似,人工神经元也互相连接并具有强大的处理能力
- 人工神经网络试图复现真实大脑的行为和过程,他们的结构是基于生物学观察而建模的
- 人造神经元也是一样的,它的结构令人想起真正的神经元结构
- 神经元结构
- 1943年生物神经元结构 → \rightarrow →简单的神经元模型:MP神经元
- 每一个神经元由一个线性拟合和一个非线性激活函数组成
- 神经元都有输入连接和输出连接 → \rightarrow →这些连接模拟大脑中突触的行为。
- 与大脑中突触传递信号的方式相同:信号从一个神经元传递到另一个神经元,这些连接也在人造神经元之间传递信息
- 每一个连接都有权重 → \rightarrow →这种模式是从大脑突触得到的启发,权重实际上模拟了生物神经元之间传递的神经物质的数量
2 FNN
- 多层感知机
- 1.单隐层感知机
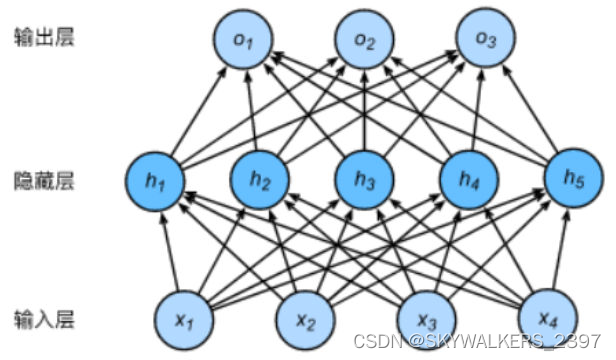
- 感知机:只有一个隐藏层,该层中有5个隐藏单元
- 隐藏层和输出层均是全连接层
- 学习过程:根据训练数据来调整神经元之间的链接权重以及每个功能神经元的阈值
- 2.多层感知机(MLP),也称前馈神经网络
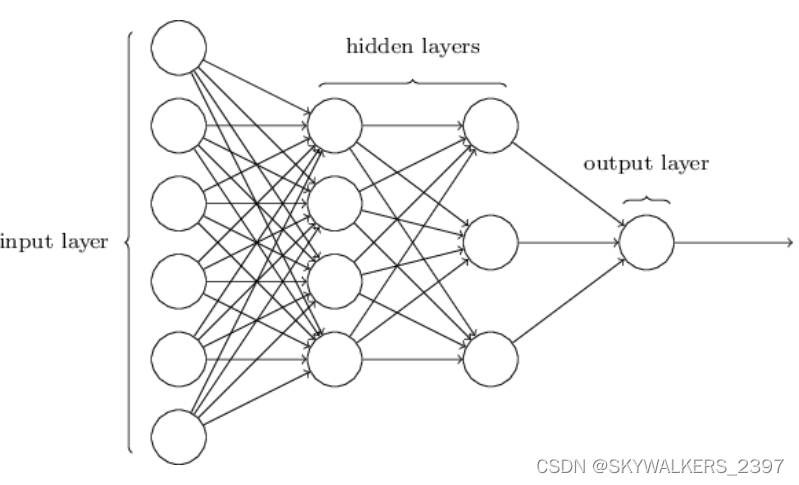
- MLP可分为3个部分:输入层(最左边),隐藏层(中间两层),和输出层(最右边)
- 隐藏层可以一层或者多层,每一层都有若干神经元组成,每个神经元承担计算功能包括线性加权和非线性变换
- 各层之间通过权值建立联系,后一层每个神经元与前一层每个神经元产生连接
- 1.单隐层感知机
3 激活函数
- 激活函数
- 激活函数是神经网络中一个至关重要的部分、其非线性使得神经网络几乎可以逼近任何非线性函数。不使用激活函数,无论神经网络多少层、其每一层输出都是上一层线性组合、即神经网络为线性模型,表达能力有限。
- 激活函数选择基本要求:连续可导、可以允许少数点上不可导。
- S型激活函数和ReLU及其变种等
- S型激活函数:Sigmoid和Tanh(饱和激活函数)
- 特点:有界、且输入绝对值越大,对应梯度就越小,越趋近于0
- sigmoid 函数是一个logistic 函数,意思就是说:不管输入是什么,得到的输出都在0 到1 之间。也就是说,你输入的每个神经元、节点或激活都会被缩放为一个介于0到1之间的值
f ( x ) = 1 1 + e − x f(x) = \frac 1{1 + e^{-x}} f(x)=1+e−x1
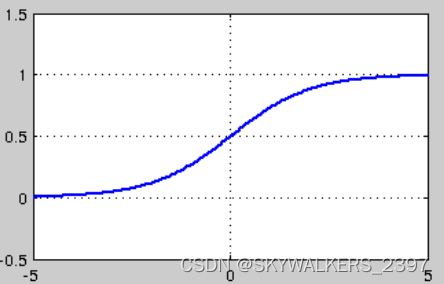
- sigmoid也有其自身的缺陷,最明显的就是饱和性(软饱和激活函数)。从上图可以看到,其两侧导数逐渐趋近于0 (梯度消失)
- sigmoid函数的输出均大于0,使得输出不是0均值,这称为偏移现象,这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入
- sigmoid函数连续,光滑,严格单调,以(0,0.5)中心对称,是一个非常良好的阈值函数
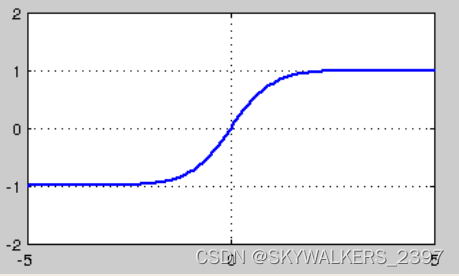
- tanh也是一种非常常见的激活函数。与sigmoid相比,它的输出均值是0,使得其收敛速度要比sigmoid快,减少迭代次数。然而,从途中可以看出,tanh一样具有软饱和性,从而造成梯度消失
- sigmoid 函数是一个logistic 函数,意思就是说:不管输入是什么,得到的输出都在0 到1 之间。也就是说,你输入的每个神经元、节点或激活都会被缩放为一个介于0到1之间的值
f ( x ) = 1 − e − 2 x 1 + e − 2 x f(x) = \frac {1 - e^{-2x}}{1 + e^{-2x}} f(x)=1+e−2x1−e−2x
2.ReLu及其变种(非饱和激活函数)
- ReLu:ReLU的全称是Rectified Linear Units,是目前深度学习模型中经常使用的激活函数
f ( x ) = { x , i f x ⩾ 0 0 , i f x < 0 f ( x ) = max ( 0 , x ) f(x) = \left\{ \begin{matrix} x,if ~~~x \geqslant0 \\ 0,if ~~~x<0 \end{matrix} \right.\\f(x) = \max(0,x) f(x)={ x,if x⩾00,if x<0f(x)=max(0,x)
- 当x<0时,输出为0,而当x>0时,则保持x不变进行输出,这个特性称:单侧抑制。所以,ReLU能够在x>0时保持梯度不衰减,从而缓解梯度消失问题
- 单侧抑制在某些情况下可能导致某个神经元“死亡”,如果某个神经元始终输出为负、则反向传播时相应梯度为0,导致无法进行有效更新 → \rightarrow →ReLU变种
- ReLU是将所有的负值都设为零,相反,Leaky ReLU是给所有负值赋予一个非零斜率(允许一定信息通过)
y i = { x i , i f x ⩾ 0 x i a i , i f x < 0 , a i 是( 1 , + ∞ ) 区间内的固定参数 y_i = \left\{ \begin{matrix} x_i,if ~~~x \geqslant0 \\ \frac {x_i}{a_i},if ~~~x<0 \end{matrix} \right.,a_i是(1,+\infty)区间内的固定参数 yi={ xi,if x⩾0aixi,if x<0,ai是(1,+∞)区间内的固定参数 - PReLU可以看作是Leaky ReLU的一个变体。在PReLU中,负值部分的斜率是根据数据来定的,而非预先定义的PReLU中的ai是根据数据变化的;Leaky
ReLU中的ai是固定的 - ELU不同于LeakyReLU和PReLU输入为负时,进行线性压缩,指数线性单元在输入为负时、进行非线性变换
f ( x ) = { x , i f x ⩾ 0 α ( e x − 1 ) , i f x < 0 f(x) = \left\{ \begin{matrix} x,~~~~~~~~~~~~~~if ~~~x \geqslant0 \\ \alpha(e^x - 1),if ~~~x<0 \end{matrix} \right. f(x)={ x, if x⩾0α(ex−1),if x<0- α> 0是一个超参数,具有调节激活值均值为0的功能,可加速神经网络收敛
- 计算量稍大,类似于Leaky ReLU,理论上虽然好于ReLU,但在实际使用中目前并没有好的证据ELU总是优于ReLU
4 训练神经网络—反向传播方法
- 神经网络的运行分三步:
- 前向传播:给定输入和参数,逐层向前进行计算,最后输出预测结果
- 反向传播:基于前向传播得到的预测结果,使用损失函数得到损失值,然后计算相关参数梯度,该计算方法称为:反向传播
- 参数更新:使用梯度下降算法对参数进行更新,重复上述过程,逐步迭代,直到模型收敛
前向传播过程:
- 通过公式层层计算网络的激活值,最终能够根据输入X得到相应的输出Y
反向传播过程:
- 以二次损失函数为例: C = 1 2 n ∑ x ∣ ∣ y ( x ) − a L ( x ) ∣ ∣ 2 C = \frac 1{2n}\sum_x||y(x) - a^L(x)||^2 C=2n1∑x∣∣y(x)−aL(x)∣∣2
- 其中n为训练样本x的总数, y = y ( x ) y = y(x) y=y(x)为期望的输出,L为网络的层数, a L ( x ) a^L(x) aL(x)为网络的输出向量
- 反向传播过程中要计算 ∂ C ∂ ω \frac {\partial C}{\partial \omega} ∂ω∂C和 ∂ C ∂ b \frac {\partial C}{\partial b} ∂b∂C
优化困境:
- 梯度消失:
- 当层数增加,最后一层误差将在前面层中快速衰减,使得靠近输入层的梯度值非常小,参数几乎无法进行有效更新,在下一次前向传播时,由于前面层的参数无法有效从数据中获得有价值信息供后面层使用,模型难以有效训练
- 局部最优与鞍点:
- 损失函数与参数之间关系为非凸,深度神经网络具有非常多的局部最优。不过往往这些局部最优都可以保证模型效果。
- 由于维度过高,神经网络模型常存在很多鞍点(梯度为0、但不是最大或最小值),影响模型收敛、陷入局部最优假象