数学建模——公交调度优化

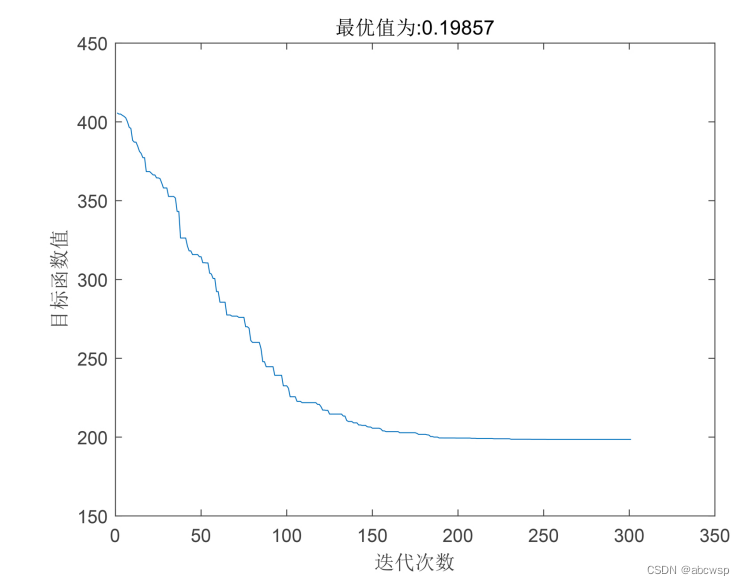
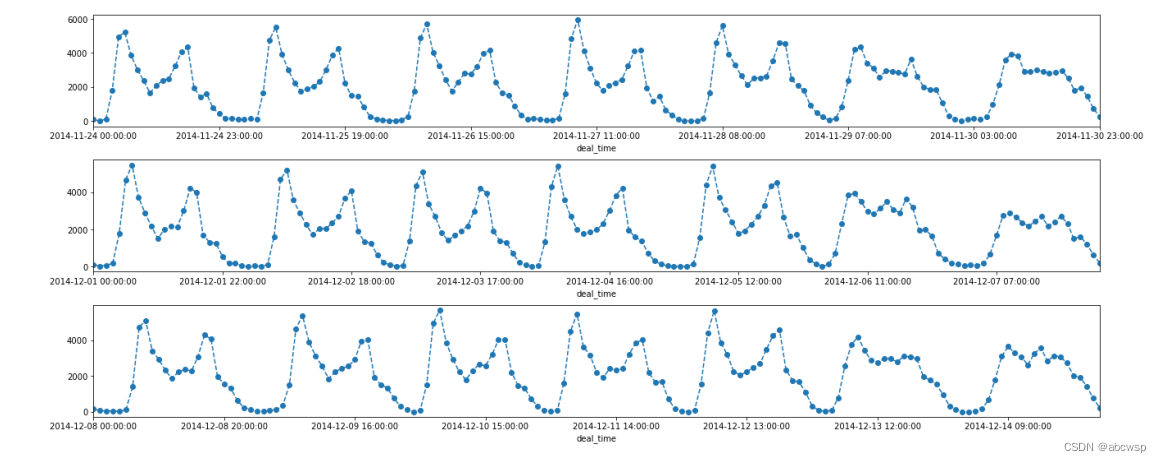
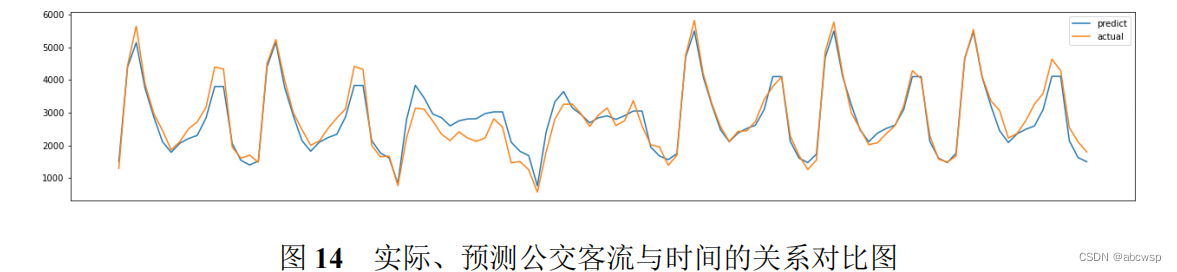
本文通过建立利润阈值模型鉴定高平峰期，综合考虑公交线路资源配置与乘客候车时间，建立多目标优化模型，通过人工免疫算法算法对公交调度方案进行优化，通过建立梯度提升树模型预测客流量，从而预测“高峰”和“平峰”时期。

考虑到市民出行并不是“均匀”的，“高峰”需要表征指的是乘客较多的时段，为了方便处理，我们将一段时间$\Delta T$内的运营总收入与运营总成本之差不小于某一个给定的“阈值”的时段。而问题的关键在于如何去建立时间与运营收入与成本的关系以及阈值的选择，本组通过建立净利润阈值模型，引进交通指数概念作为阈值选择的依据，从而合理定义了“高峰”与“平峰”的划分依据。\par

净利润阈值模型

考虑到运营公交车的成本有诸多因素，包括一段时间内可变成本$\tilde{C}$——耗油量、磨损因度等，以及固定成本$\overline{C}$——司机工资以及购车费用，这里我们考虑为了判别高峰期或平峰期，本组首先将发车时间划分为若干紧密区间，对每个划分区间进行观测其净利润是否达到阈值：
$$\Omega =\left[T_0,T_1\right]\cup \left[T_1,T_2\right]\cup \cdots \cup \left[T_{N-1},T_N\right]$$
其中划分区间长度为：$\Delta T=T_n-T_{n-1}$
设第$i$班次行驶时间记为:$[t_i,t_i+t_{total}]$，因而每一班次在抽样划分区域$\left[T_n,T_{n+1}\right]$上消耗的费用为$c_n^i$：
$$c_n^i=\{\begin{array}{l}\left[\min \left(T_{n+1},t_{i+1}\right)-\max \left(T_n,t_i\right)\right]\cdot v\cdot f{T}_n⩽t_{i+1}and{T}_{n+1}⩾t_i\\ 0T_n>t_{i+1}or{T}_{n+1}<t_i\end{array}$$
其中，第$i$班次的公交起始时刻为$t_i$：
$$t_i=T_0+\left(i-1\right)\Delta t_{i-1}$$
则抽样划分区域$\left[T_n,T_{n+1}\right]$上消耗的可变成本总费用为：
$$\Delta {\tilde{C}}_N=\sum _{i=1}^M{c}_N^i$$

因此，抽样划分区域 $[T_n,T_{n+1}]$上消耗的总费用 $C$ 为：
$$\Delta C=\Delta \tilde{C}+\Delta \overline{C}$$
考虑到收入的影响因素为乘客的到达率，设第$j$个站点乘客随时间的变化的到达率为$r_j$，假设$r_j$服从均匀分布(人/分钟)，则抽样划分区域$ \left[ T_{n},T_{n+1} \right]$上的总收入为：
$$\Delta I=P\cdot \sum _{\Delta t}\Delta t\cdot r_j$$

问题2的模型建立

假设乘客到达率服从均匀分布即：
$$r_j\sim U\left(t_{j-1},t_j\right)$$
乘客的平均等车时间为：
$$\bar{t}=\frac{t_i-t_{i-1}}{2}$$
设第$i$辆车发车时间为$T_i$，第$i$辆车到达（或离开）第$j$站的时刻为：$T_i^j$则:
$$T_i^j=\{\begin{array}{l}{T}_i+{\sum }_{n=2}^j{d}_{n}j>1\\ T_{i}j=1\end{array}$$
考虑到顾客的时间利益、服务满意程度，引进候车超时率$WT$表现客户端的方便程度:
$$WT=\frac{\text{候车时间超过}15\text{分钟的总人数}}{\text{调度期内上车总人数}}$$
即为：
$$WT=\frac{\sum _{T_i^j}\sum _{h=1}^{h_{ij}}\left\{W_i^j\left(h\right)|W{T}_{ij}\left(h\right)⩾15\right\}}{\sum _{T_i^j}{P}_i\left(T_i^j\right)}$$
式中$W_i^j(h)$表现第$i$辆车到达第$j$站时，该站上已经等待过$h$辆车，却仍未上车的人数，设这些人已经等待时间为:
$$W{T}_i^j\left(h\right)=T_i^j-T_{i-h}^j,W_i^j\left(0\right)=U_{ij}$$
式中$U_i^j$表示在$T_{i-1}^j$到$T_i^j$时间段内，新来到车站等车的人数:
$$W{W}_i^j\left(0\right)={\int }_{T_{i-1}^j}^{T_i^j}{u}_i\left(t\right)dt$$
设$h_{ij}$表示第$k$辆车到达$j$站时，该站上等待最久乘客的候车辆数，则第$i$辆车离开第$j$站时车上的乘客数可表示为：
$$P_i\left(T_i^j\right)=\{\begin{array}{ll}{a}_{ij}+{\sum }_{r=0}^{h_{ij}}{W}_i^j\left(r\right),& h_{ij}^{\ast }=0,\\ M,& h_{ij}^{\ast }>0.\end{array}$$
其中$a_{ij}$为第$i$辆车到达第$j$站后，等乘客下车后，车上的剩余乘客数:
$$a_{ij}=\max \left\{\left(P_k\left(T_i^{j-1}\right)-D_j\right)\text{，}0\right\}$$
式中$D_j$为在第$j$站下车的乘客数。
设$M$为车辆最大承载人数，则此时可容纳的上车人数记为：
$$b_{ij}=M-a_{ij}$$
基于先到先上车的排队原则，在第$k+1$辆车到达第$j$站站时，仍然要等候车辆的最大等待次数$h_{ij}^{\ast }$:
$$h_{ij}^{\ast }=\max \left\{h|\sum _{r=0}^{h_{ij}}{W}_{ij}\left(r\right)⩽b_{ij}\right\},$$