【GNN】谱域图卷积

谱域图卷积

1. 谱域卷积的背景知识

1.1 谱域图卷积实现思路

$$f_1(t)\star f_2(t)=F^{-1}[F_1(w)F_2(w)]$$

1.2 如何定义图上的傅里叶变换

经典傅里叶变换：
$$x(t)=\frac{1}{n}\sum _{w=0}^{n-1}{e}^{i\frac{2\pi }{n}tw}X(w)$$
图傅里叶变换：
$$x(\dot{i})=\sum _{l=1}^n\hat{x}({\lambda }_l)u_l(\dot{i})$$

1.3 拉普拉斯矩阵

$$L=D-W$$
拉普拉斯矩阵是对称半正定矩阵， 对称半正定矩阵具有以下性质：

• n阶对称矩阵一定有n个线性无关的特征向量
• 对称矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。
• 实对称矩阵的特征向量一定是实向量
• 半正定矩阵的特征值一定是非负的

$$L=U\Lambda U^{-1}=U\Lambda U^{\top }$$

1. 4 图的拉普拉斯算子

$$\begin{array}{rl}\Delta f_i=& \sum _{(i,j)\in e}{W}_{ij}(f_i-f_j)\\ =& \sum _{j=1}^n{W}_{ij}(f_i-f_j)\\ =& D_{ii}{f}_i-\sum _{j=1}^n{W}_{ij}{f}_j\end{array}$$
可以理解为中心节点依次减去周围节点，然后乘以权重后求和。

• 公式里的 $D_{ii}$ 表示度矩阵的分量，有连接为1，没有连接为0

对于 n 个节点有

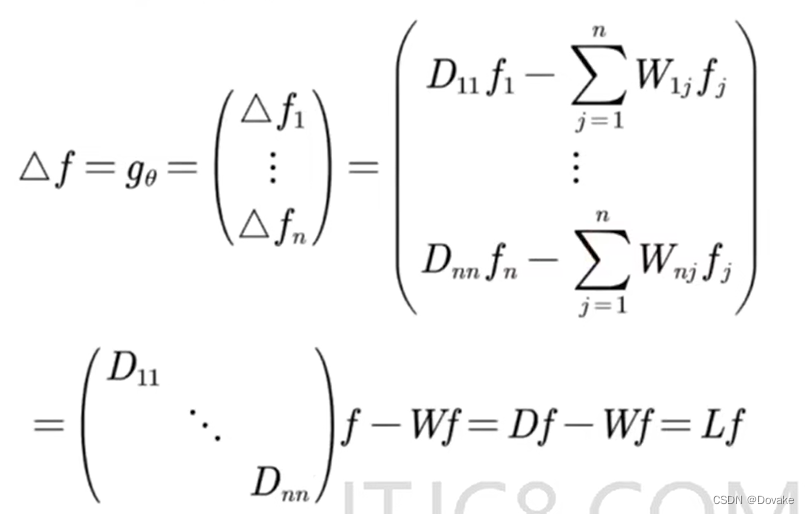
2. 图傅里叶变换

2.1 图节点表示

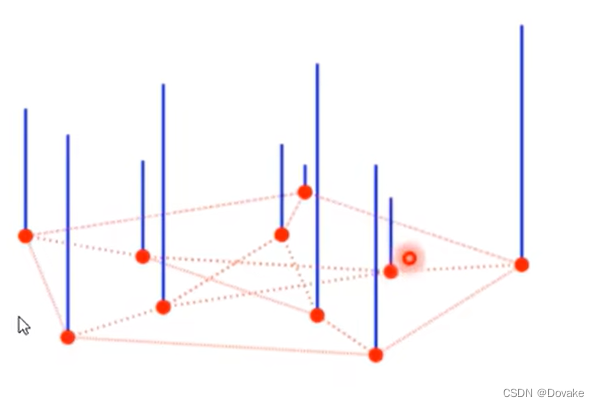
图上的信号一般可以表示为一个向量，假设有n个节点，则可以记作：
$$x=[x_1\dots x_n{]}^{\top }\in {\mathbb{R}}^n$$

2.2 图傅里叶变换

傅里叶变换的本质是：把任意一个函数表示成了若干个正交基函数的线性组合。

$$\begin{array}{rl}f(t)=& F^{-1}[F(w)]={\int }_{\mathbb{R}}F(t)e^{i2\pi wt}\\ f(t)=& \frac{1}{n}\sum _{w=1}^{n}F(w)e^{i\frac{2\pi }{n}wt}\end{array}$$

• 对应图上的信号x 如果要进行一个傅里叶变换，很自然我们能想到我们也要找到一组正交基，通过这组正交基的线性组合来表达。
• 在图傅里叶变换函数的正交函数，其实是使用拉普拉斯矩阵的特征向量作为基函数。