关系型数据库（二）---关系代数

---

前言

本文主要讲解了关系代数

---

一、关系代数

1.关系操作

关系操作是集合操作，操作的对象及结果都是集合，是一次一集合（Set-at-a-time）的方式。而非关系型的数据操作方式是一次一记录（Record-at-a-time）

关系模型与其他模型相比，最有特色的是它的数据库语言。这种语言灵活方便、表达能力和功能都很强。

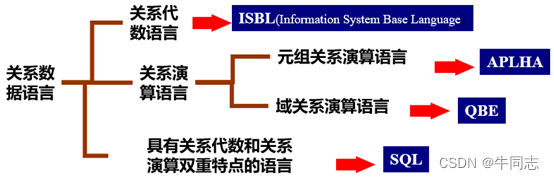
目前关系数据库所使用的语言一般都具有定义、查询、更新和控制一体化的特点，而查询是最主要的部分。

所以说，关系数据库的核心部分是查询，故又称为查询语言，而查询的条件要使用关系运算表达式来表示。

因此，关系运算是设计关系数据语言的基础。

按表达查询的方法不同，关系运算可分为关系代数和关系演算两大类。

2.关系代数

关系代数是一种抽象的查询语言，它用对关系的运算来表达查询

关系代数

1.运算对象是关系
2.运算结果亦为关系

关系代数的运算符有两类：集合运算符和专门的关系运算符
传统的集合运算是从关系的“水平”方向即行的角度进行，专门的关系运算不仅涉及行而且涉及列

二、集合运算

传统集合运算 :

1.并
2.差
3.交
4.笛卡尔积

专门的关系运算:

1.选择运算 
2.投影运算 
3.连接运算 
4.除运算

1.传统集合运算

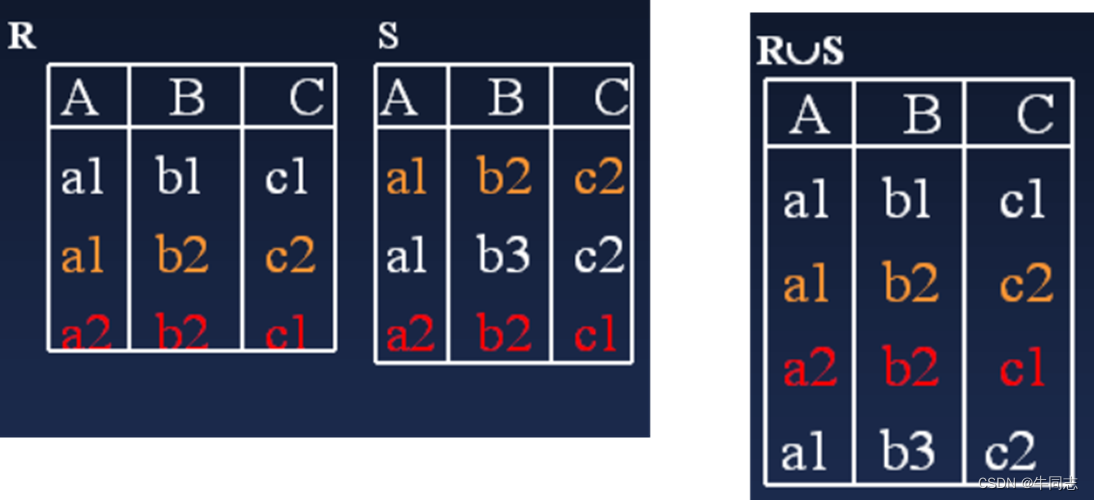
（1）并运算

所有至少出现在两个关系中之一的元组集合。
R ⋃ S = { t ∣ t ∈ R ∪ ∈ t ∈ S } R\bigcup S =\{ t | t\in R\cup \in t\in S \} R⋃S={ t∣t∈R∪∈t∈S}
两个关系R和S若进行并运算，则它们必须是相容的：

1.关系R和S必须是同元的，即它们的属性数目必须相同。
2.对任意i，R的第i个属性的域必须和S的第i个属性的域相同。

（2）差运算

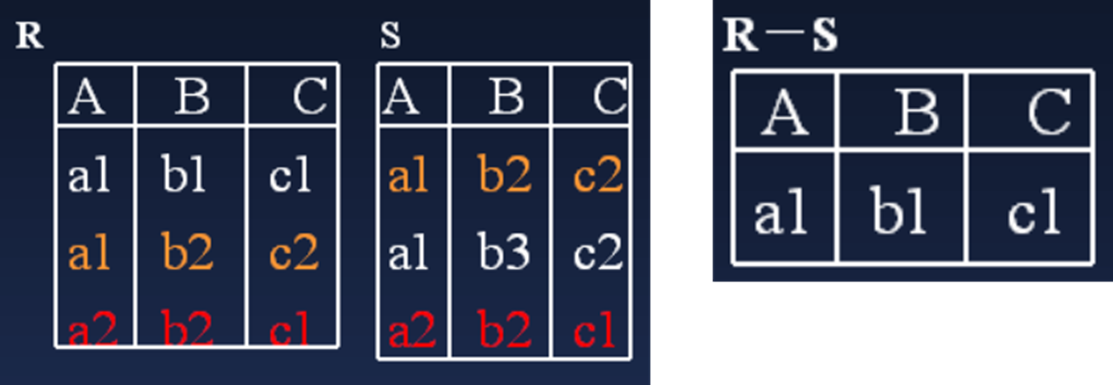
设关系R和S具有相同的关系模式，R和S的差是由属于R但不属于S的元组构成的集合，记为：

R − S = { t ∣ t ∈ R ∩ t ∉ S } R-S =\{ t | t\in R\cap t\notin S \} R−S={ t∣t∈R∩t∈/S}
Ｒ与Ｓ必须是相容的

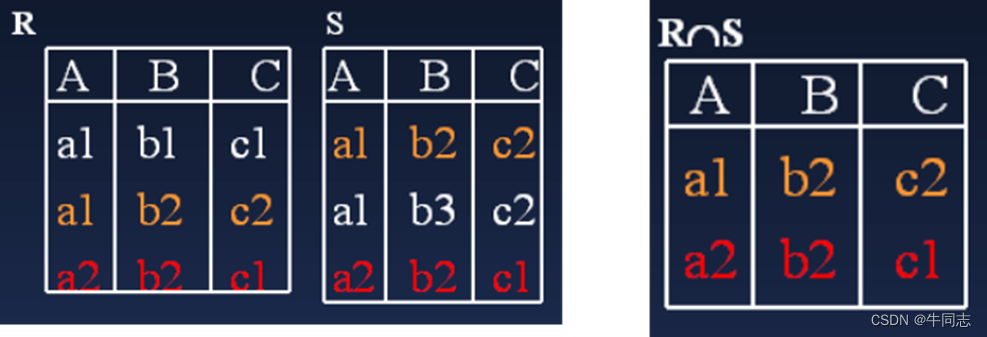
（3）交运算

既属于R又属于S的元组。记为：
R ∩ S = { t ∣ t ∈ R ∩ t ∈ S } R\cap S =\{ t | t\in R \cap t\in S \} R∩S={ t∣t∈R∩t∈S}

关系的交可以用差来表示，即
$$R\in S=R-(R-S)$$

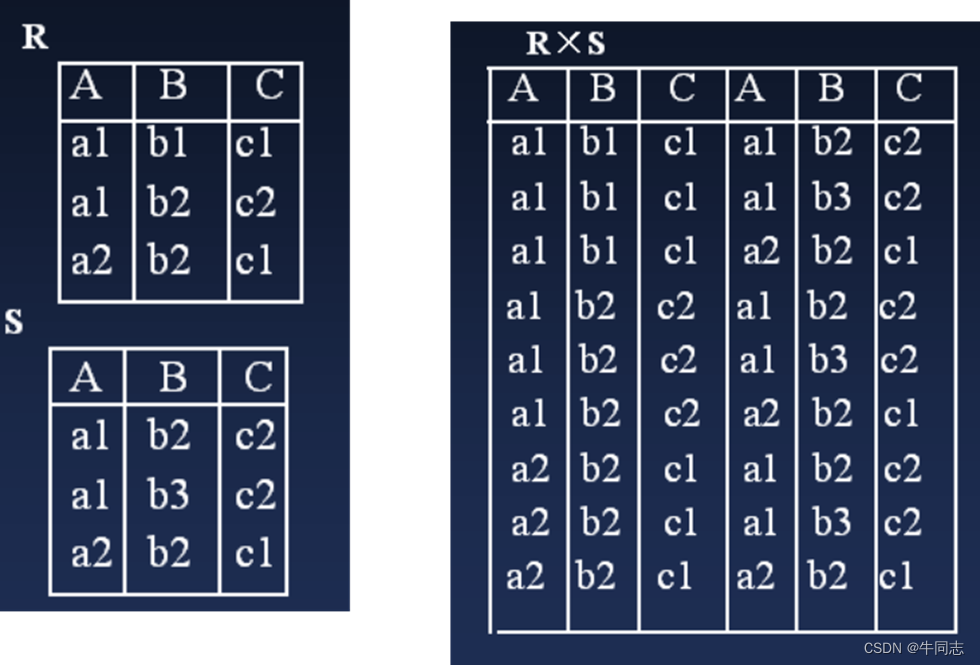
（4）笛卡儿积

两个分别为n目和m目的关系R和S的笛卡尔积是一个$(n+m)$列的元组的集合。元组的前n列是关系R的一个元组，后m列是关系S的一个元组。若R有$k_1$个元组，S有$k_2$个元组，则关系R和关系S的笛卡尔积有$k_1\times k_2$个元组。记为：
R × S = { t r t s ^ ∣ t r ∈ R ∩ t s ∈ S } R\times S=\{\widehat{t_rt_s}|t_r\in R\cap t_s\in S\} R×S={ tr​ts​ ​∣tr​∈R∩ts​∈S}
$R\times S$的度为R与S的度之和，
$R\times S$的元组个数为R和S的元组个数的乘积。

2.专门的关系运算

（1）选择运算

从关系中找出满足给定条件的所有元组。
δ F ( R ) = { t ∣ t ∈ R , F ( t ) = ‘真’ } \delta_F(R)=\{t | t\in R , F(t) = ‘真’\} δF​(R)={ t∣t∈R,F(t)=‘真’}
从行的角度进行的运算，即水平方向抽取元组。

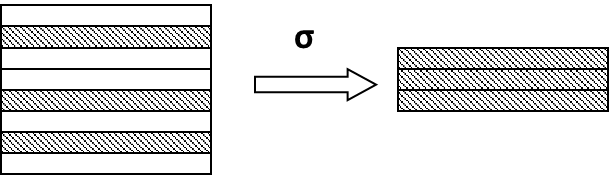
经过选择运算得到的结果可以形成新的关系，其关系模式不变， 但其中元组的数目小于或等于原来的关系中的元组的个数，它是原关系的一个子集。

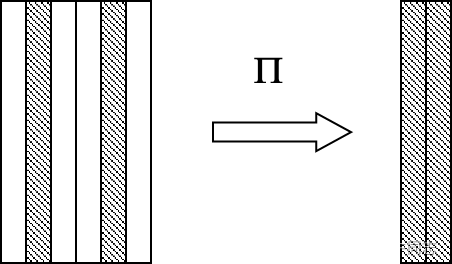
（2）投影运算

从关系中挑选若干属性组成的新的关系 。
Π A ( R ) = { t [ A ] ∣ t ∈ R } , A ⊆ R \Pi_A(R) = \{ t[A] | t\in R \} , A\subseteq R ΠA​(R)={ t[A]∣t∈R},A⊆R
从列的角度进行的运算，即垂直方向抽取元组。
投影的结果中要去掉相同的行。

（3）连接运算

从两个关系的笛卡尔积中选取属性间满足一定条件的元组
R ⋈ A θ B S = { t r t s ^ ∣ t r ∈ R ∩ t s ∈ S ∩ t r [ A ] θ t s [ B ] } θ 为算术运算 , 为等号时称为等值连接。 A , B 为 R 和 S 上度数相等且可比的属性列。 R\Join_{A\theta B} S = \{\widehat{t_rt_s}|t_r\in R\cap t_s\in S\cap t_r[A]\theta t_s[B] \} \theta为算术运算,为等号时称为等值连接。 A,B为R和S上度数相等且可比的属性列。 R⋈AθB​S={ tr​ts​ ​∣tr​∈R∩ts​∈S∩tr​[A]θts​[B]}θ为算术运算,为等号时称为等值连接。A,B为R和S上度数相等且可比的属性列。
从定义上可以看出联接运算就是在两个关系的笛卡尔积上进行的选择运算。

条件连接

关系R和S，求$R{\bowtie }_{C=E}S$

下表为R

下表为S

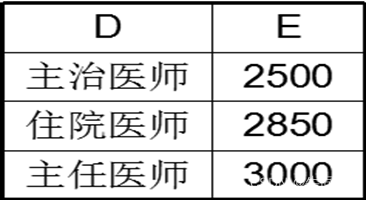
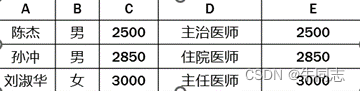
结果为：

等值连接

θ为“＝”的连接运算称为等值连接

有：

自然连接（Natural join）（特殊）
左连接（Left Join）
右连接（Right Join）

自然连接

操作步骤：

1.选择同时出现在R和S中属性相等元组；
2.去掉重复属性。    

可以看出，如果两个关系没有公共属性，自然连接就是笛卡尔积。
下表为R

下表为S

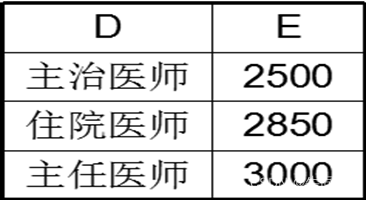
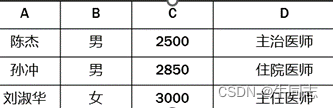
结果为：

左连接与右连接

左连接（Left Join）
R左连接S：所有来自R的元组和那些连接字段相等处的S的元组。

右连接（Right Join）
R右连接S：所有来自S的元组和那些连接字段相等处的R的元组。

表R：

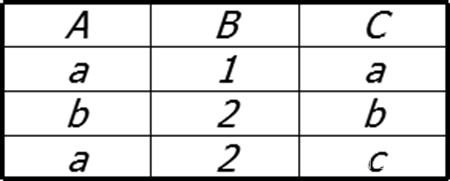
表S:

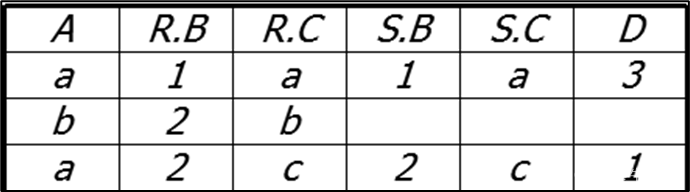
R左连接S的结果为：

R.B=S.B ∧ R.C=S.C

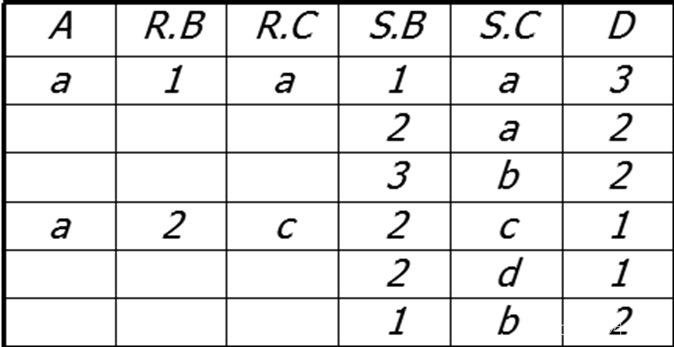
R右连接S的结果为：
R.B=S.B ∧ R.C=S.C

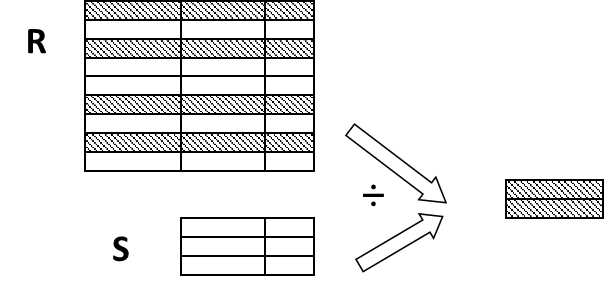
（4）除运算

象极

给定一个关系R(X,Z)，X和Z为属性组。当t[X]=x时，x在R中的象集(Images Set)为：
Z x = { t [ Z ] ∣ t ∈ R , t [ X ] = x } Z_x=\{t[Z]|t\in R,t[X]=x\} Zx​={ t[Z]∣t∈R,t[X]=x}
它表示R中属性组X上值为x的诸元组在Z上分量的集合。

关系R中，A可以取四个值{a1,a2,a3,a4}：

    a1的象集为 {(b1,c2)，(b2,c3)，(b2,c1)}
　	a2的象集为 {(b3,c7)，(b2,c3)}
	a3的象集为 {(b4,c6)}
　	a4的象集为 {(b6,c6)}

运算

给定关系R(X，Y)和S(Y，Z)，其中X，Y，Z为属性组。R中的Y与S中的Y可以有不同的属性名，但必须出自相同的域集。R与S的除运算得到一个新的关系P(X)，P是R中满足下列条件的元组在X属性列上的投影：元组在X上分量值x的象集$Y_x$包含S在Y上投影的集合。

R ÷ S = { t r [ X ] ∣ t r ∈ R ∩ π Y ( S ) ⊆ Y x } Y x ： x 在 R 中的象集， x = t r [ X ] R÷S =\{t_r [X] | t_r \in R\cap \pi_Y (S) \subseteq Y_x \} \\Y_x：x在R中的象集，x = t_r[X] R÷S={ tr​[X]∣tr​∈R∩πY​(S)⊆Yx​}Yx​：x在R中的象集，x=tr​[X]

例子1

R1表：

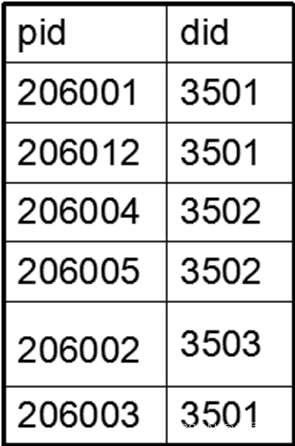
R2表：

R1÷R2的结果：

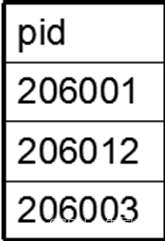
例子2

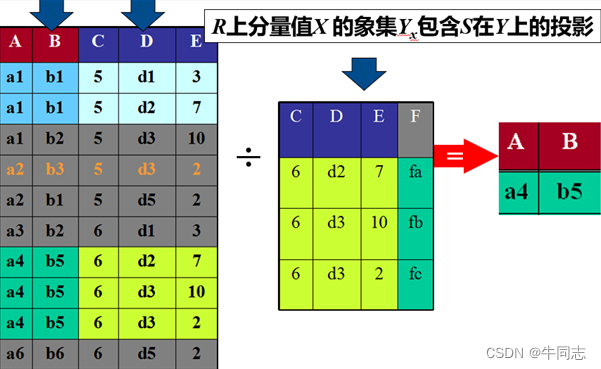
3.查询优化

将一个关系代数表达式转换为另一个具有较高效率的关系代数表达式的过程称为“查询优化”。

（1）优化准则

① 提早执行选择运算。
② 合并笛卡尔积与其后的选择运算为连接运算。
③ 将投影运算与其后的其他运算同时进行，以避免重复扫描关系。
④ 将投影运算和其前后的二目运算结合起来，以避免为去掉某些字段再扫描一遍关系。
⑤ 执行连接前对关系适当地预处理．就能快速地找到要连接的元组。
⑥ 存储公共子表达式。

---

总结

文章的不妥之处请读者包涵指正