DDPM:Denoising Diffusion Probabilistic Model,去噪扩散概率模型
本文参考:一个视频看懂扩散模型DDPM原理推导|AI绘画底层模型_哔哩哔哩_bilibili
1、大概原理
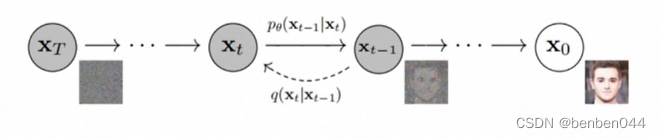
从右往左为正向加噪过程,从左往右
为逆向降噪过程。
在正向过程中不断加噪,经过T次之后得到,我们希望
这样在推理过程中,我们可以从 随机取出
(加‘ 表明这个是新值)。
如果我们能学得的降噪方法,就可以最终通过
的新图片。
2、扩散模型的降噪方法预测什么
现在就是需要学的降噪方法,DDPM算法不是直接学预测
值的方法,而是预测
的条件概率分布
,然后从分布中取值得到
的值。此方法类似于deepar预测方法,预测的是分布而不是值。
那么为什么去预测分布而不是确切的的值?
因为有了分布之后就可以采样取出,模型就有了随机性。
进一步,假如得到,就可以抽样得到
,这样一步步下去就可以从
。所以,我们要学习的是p的分布,而不是确切的某张图。
结论:学习过程全程是在预测分布p。
后续我们会看到模型在预测噪音,这个噪音不是和
之间的噪音,而是正态分布p中的
计算时涉及到的噪音
。
所以,我们通过预测得到
,进而得到p。也验证了我们的结论,即:学习过程全程是在预测分布p。
3、条件概率分布的拆解
公式1:,根据贝叶斯公式对最初的条件概率分布进行了转换,新得到的算式包含了3个概率分布。
(1)第1个p的计算
第1个p为:
从到
为加躁过程中的概率分布,因为加躁过程是事先定义的,所以概率分布p也是可以被定义的。
现在我们定义加躁过程如下:
公式2:,其中
的噪音,
。
因为,所以
。(ps:方差需要取平方)
可以看出为噪音的方差,它需要非常小接近0。只有加的噪音很小,前向、后向才是服从正态分布的。
进一步推导,,即:
公式3:。
(2)第3个p的计算
第3个p为:,它和第2个p是类似的。如果找到一个的计算方法,那么另一个也可以类似得到。
上一步我们得到每一步加躁过程的公式2,以及每一步加躁的条件概率分布公式3。
针对加躁过程,,所以理论上可以用
来推导出
。
对公式1进行改造:
公式4:
因为加躁过程是马尔可夫过程,所以只跟前一步有关,和再前一步无关,即和
也无关,所以
而是从
一步步得到
,所以不能再做简化。进而,公式4简化为:
公式5:
现在重新开始计算新的第3个p的值,从公式2开始推导如下(ps:括号表示其中含有部分参数但是未写出来,省略不重要的信息):
最后,经过不严谨的推导我们给出官方结果:
公式6:,其中
表示连乘。
(3)扩散公式求解
上一步求得,那么也可以类似求得
。
直接给出公式4的官方结果:
公式7:
其中是超参,
的公式见如下:
公式8:
因为固定,所以求
的任务就变成了求
。
如果有了,那么根据如下公式可以得到预测的推理值:
公式9:,
如果直接根据公式7从中取出一个
,该过程是不可导的(直接通过python包输入均值、方差取值的方式),那么逆向过程有问题,所以通过重参数技巧转换为公式9这样一个可求导的公式来表达
。
在推理阶段就是我们最终想要的值,该值未知,所以需要转换为已知因子的公式。
公式6经过重参数技巧转换后如下:
公式10:,进而得到:
公式11:,这其中的t为当前加噪阶段数,会变化。同时,这个
是中间过程的参数值,不可以作为最终的预测值,因为推理的p过程需要遵循马尔可夫过程,所以必须一步步推导到
。
在公式7中,未知值是,而该值中的未知值是
,而
中的未知值是
,该值无法通过现有公式计算推导得到。
于是我们借助UNet网络,输入,输出
。
将公式11代入公式8,可得到:
公式12:,公式中除了
其他均为已知。
而是通过UNet网络预测出来的,可以表示为
,
为UNet模型参数。
*************扩散模型通过UNet网络得到预测图像的过程**************:
以上就是扩散模型DDPM最重要的逻辑。
4、模型训练
根据公式12可知,UNet网络训练的是正态分布的噪音。
问题1:模型训练时的输入输出?
答案:输入,输出
。
问题2:那么哪个过程进行UNet网络参数的训练呢?
答案:加噪过程。加噪过程是训练阶段,降噪过程是推理阶段。
根据公式2可知,加噪过程的噪音是实现定义好的,所以我们可以比较预测的噪音和真实
的KL散度计算loss值,在官方说明中KL散度公式一通推导后可简化为计算这两个值的mse值。
问题3:训练时是否正向一步步推导的?
答案:不需要。在训练过程中,根据公式10 可知,
可以通过
,
,
,
这4个值计算得到。
可以提前计算好放在内存中,
就是输入输入的图片集,
就是输入的噪音,
是加噪阶段数。
所以正向中每一步皆可直接获取值。
5、训练和推理的伪代码实现
(1)训练阶段

解读:
表示从数据集中取出图片
表示随机抽取一个加噪阶段数,如之前所述,加噪过程不需要一步步来。
为
(2)推理阶段

解读:
表示逆向过程需要一步步来的。
第4步的复杂计算对应公式9,计算中的第一个公式对应公式12。