大数据算法自检

1 大数据亚线性空间算法

1.1 流模型的计数问题

问题定义？用什么算法？算法步骤？(提示：三层递进)

切比雪夫不等式？怎么证明？期望，方差，空间复杂度？

极其有限的空间存储极大的数目

morris，morris+，morris++

$1/(2^X)$ => $\hat{f}=(2^X-1)$

$E[\gamma ]=N$

$D[\gamma ]=\frac{N^2-N}{2k}$。

$P[|\gamma -N|\ge ϵ]⩽\frac{N^2-N}{2k{ϵ}^2}$

1.2 不重复元素数

问题定义？用什么算法？算法步骤？
(提示：存储实数：三层递进 + 无法存储实数：1+1)

怎么证明？期望，方差，空间复杂度？

统计一个数据流的不重复元素数

1. FM，FM+

   $h:[n]\mapsto [0,1]$ => z = m i n { z , h ( i ) } z=min\{z,h(i)\} z=min{ z,h(i)} => $\frac{1}{z}-1$

   $E[Z]=\frac{1}{d+1}$

   $var[Z]⩽\frac{2}{(d+1)(d+2)}\frac{1}{q}<\frac{2}{(d+1)(d+1)}\frac{1}{q}$

   $P[|X-d|>{ϵ}^{\prime }d]<\frac{2}{q}(\frac{2}{{ϵ}^{\prime }}+1{)}^2$

2. FM’+

   维护当前看到的最小的k个哈希值，返回$\frac{k}{z_k}$

3. PracticalFM

   1. 如果$zeros(h(j))>z$：$z=zeros(h(j))$

   2. 返回$\hat{d}=2^{z+\frac{1}{2}}$

   $E[Y_r]=\frac{d}{2^r}$

   $var[Y_r]\le \frac{d}{2^r}$。

   最终正确的概率应该大于$1-\frac{2\sqrt{2}}{C}$。

4. BJKST

   1. 若$zeros(h(j))>z$

      1. $B=B\cup (g(j),zeros(h(j)))$
      2. 若$|B|>\frac{c}{{ϵ}^2}$
         1. $z=z+1$
         2. 从B中删除$(\alpha ,\beta )$，其中$\beta <z$

   2. return $\hat{d}=|B|2^z$

1.3 点查询

问题定义？用什么算法？算法步骤？

空间复杂度？

计算流中所有的元素出现次数

1. Misra_Gries

   维护一个集合A，其中的元素是$(i,\widehat{f_i})$

   1. $A\leftarrow \varnothing$

   2. 对每一个数据流中的元素e

      if e∈A，令$(e,\widehat{f_e})\to (e,\widehat{f_e}+1)$

      else if $|A|<\frac{1}{ϵ}$：将(e,1)插入A

      else

      1. 将所有A中计数减1
      2. if $\widehat{f_j}=0$：从A中删除(j,0)

   3. 对于查询 i，如果$i\in A$，返回$\widehat{f_i}$，否则返回0

   空间代价是$O({ϵ}^{-1}logn)$

2. Metwally

   1. 对每一个数据流中的元素e
      1. if e∈A：令$(e,\widehat{f_i})\leftarrow (e,\widehat{f_i}+1)$
      2. else if $|A|<\frac{1}{ϵ}$：将(e,1)插入A
      3. else 将(e,MIN+1)插入A，并删除一个满足$\widehat{f_e}=MIN$
   2. 查询 i，如果$i\in A$，返回$\widehat{f_i}$，否则返回MIN

   空间代价是$O({ϵ}^{-1}logn)$

3. Count-Min

   1. 随机选择 t 个2−wise独立哈希函数 $h_i:[n]\to [k]$

   2. 对每一个出现的更新(j,c)进行如下操作

      for i=1 to t

      ​ $C[i][h_i(j)]=C[i][h_i(j)]+c$

   3. 针对对于a的查询，返回 $\widehat{f_a}={\min }_{1\le i\le t}C[i][h_i(a)]$

4. Count-Median（min变median）

5. Count Sketch

   1. 随机选择1个2−wise独立哈希函数$h:[n]\to [k]$

   2. 随机选择1个2−wise独立哈希函数$g:[n]\to -1,1$

   3. 对于每一个更新(j,c)

      $C[h(j)]=C[h(j)]+c\ast g(j)$

   4. 针对查询a，返回$\hat{f}=g(a)\ast C[h(j)]$

6. Count Sketch+
   （相当于是将Count Sketch算法运行了t次，最后取了中值）

   1. 随机选择1个2−wise独立哈希函数 $h_i:[n]\to [k]$

   2. 随机选择1个2−wise独立哈希函数 g i : [ n ] → { − 1 , 1 } g_i:[n] \rightarrow \{-1,1\} gi​:[n]→{ −1,1}

      对于每一个更新(j,c)

      ​ 对于$i:1\to t$

      ​ $C[h_i(j)]=C[h_i(j)]+c\ast g_i(j)$

   3. 返回$\hat{f}=media{n}_{1\le i\le t}{g}_i(a)C[i][h_i(a)]$

1.4 频度矩估计

问题定义？用什么算法？算法步骤？

期望，方差，空间复杂度？

略

1.5 固定大小采样

问题定义？用什么算法？算法步骤？

期望，方差，空间复杂度？

水库抽样算法

1. 使用数据流的前s个元素对抽样数组进行初始化
   $A[1,...,s],m\leftarrow s$
2. 对于每一个更新x
   1. x以$\frac{s}{m+1}$概率随机替换A中的一个元素
   2. m++

1.6 Bloom Filter

问题定义？用什么算法？算法步骤？

大数据集中划出一个小数据集，抽一个数，猜它是否属于小数据集

1. 近似哈希

   1. 令H是一族通用哈希函数：$[U]\to [m]，m=\frac{n}{\delta }$
   2. 随机选择 h∈H，并维护数组A[m]，S的大小是n
   3. 对每一个 i∈S，$A[h(i)]=1$
   4. 给定查询q，返回yes当且仅当$A[h(i)]=1$

2. Bloom Filter

   1. 令H是一族独立的理想哈希函数：[U]→[m]

   2. 随机选取$h_1,...,h_d\in H$，并维护数组A[m]

   3. 对于每一个i∈S

      ​ 对于每一个j∈[1,d]

      ​ $A[h_j(i)]=1$

   4. 给定查询q，返回yes当且仅当$\forall j\in [d],A[h_j(q)]=1$

2 大数据亚线性时间算法

2.1 求连通分量的数目

问题定义？用什么算法？算法步骤？

计算公式？时间复杂度？

如果搜索到的点的个数少于$\frac{2}{ϵ}$就继续搜索，否则直接返回$\frac{2}{ϵ}$。

从节点集合中随机选出$r=b/{ϵ}^2$个节点构成节点U，对每个节点应用这个算法

最终的$\hat{C}=\frac{n}{r}{\sum }_{u\in U}\frac{1}{\widehat{n_u}}$，时间复杂度为$O(d/{ϵ}^3)$

2.2 近似最小支撑树

问题定义？用什么算法？算法步骤？

计算公式？时间复杂度？

G的子图$G^{(i)}=(V,E^{(i)})$，$E(i)=\{(u,v)|w_{uv}\le i\}$，连通分量的个数为C(i)

M为所有这样的子图的连通分量的数目的和：$M=n-w+{\sum }_{i=1}^{w-1}{C}^{(i)}$
$$\begin{array}{rl}M& =\sum _{i=1}^{w}i\cdot {\alpha }_i=\sum _{i=1}^w{\alpha }_i+\sum _{i=2}^w{\alpha }_i+\cdots +\sum _{i=w}^w{\alpha }_i\\ & =C^{(0)}-1+C^{(1)}-1+\cdots +C^{(w-1)}-1\\ & =n-1+C^{(1)}-1+\cdots +C^{(w-1)}-1\\ & =n-w+\sum _{i=1}^{w-1}{C}^{(i)}\end{array}$$

2.3 求点集合的直径

问题定义？用什么算法？算法步骤？

计算公式？时间复杂度？

The Indyk’s Algorithm

1. 任选$k\in [1,m]$
2. 选出$l$，使得$\forall i,D_{ki}\le D_{kl}$
3. 返回$(k,l),D_{kl}$

2.4 计算图的平均度算法

Alg III

1. 从V中抽取样本S，$|S|=\tilde{O}(\frac{L}{\rho {ϵ}^2}),L=poly(\frac{logn}{ϵ}),\rho =\frac{1}{t}\sqrt{\frac{ϵ}{4}\cdot \frac{\alpha }{n}}$
2. $S_i\leftarrow S\cap B_i$
3. f o r   i ∈ { 0 , … , t − 1 }   d o \boldsymbol{for}\ i \in \{0,\dots,t-1\}\ \boldsymbol{do} for i∈{ 0,…,t−1} do
   1. $\mathbf{if}|S_i|\ge {\theta }_{\rho }\mathbf{then}$
      1. ${\rho }_i\leftarrow \frac{|S_i|}{|S|}$
      2. $estimate{\Delta }_i$
   2. $\mathbf{else}$
      1. ${\rho }_i\leftarrow 0$
4. $\mathbf{return}\hat{\bar{d}}={\sum }_{i=0}^{t-1}(1+{\Delta }_i){\rho }_i(1+\beta {)}^i$

Alg IV

1. $\alpha \leftarrow n$
2. $\hat{\bar{d}}<-\infty$
3. $\mathbf{while}\hat{\bar{d}}<\alpha \mathbf{do}$
   1. $\alpha \leftarrow \alpha /2$
   2. $\mathbf{if}\alpha <\frac{1}{n}\mathbf{then}$
      1. $\mathbf{return}0;$
   3. $\hat{\bar{d}}\leftarrow AlgII{I}_{\sim \alpha }$
4. $\mathbf{return}\hat{\bar{d}}$

算法相关指标

近似比：$(1+ϵ)$

运行时间：$\tilde{O}(\sqrt{n})\cdot poly({ϵ}^{-1}logn)\sqrt{n/\bar{d}}$

3 并行计算算法

3.1 构建倒排索引

问题定义？Map函数做什么？Reduce函数做什么？

给定一组文档，统计每一个单词出现在哪些文件中

map：$<docID,content>\to <word,docID>$
reduce：$<word,docID>\to <word,listofdocID>$

3.2 单词计数

问题定义？Map函数做什么？Reduce函数做什么？

给定一组文档，统计每一个单词出现的次数

• Map函数：<docID,content>→<word,1>
• Reduce函数：<word,1>→<word,count>

3.3 检索

问题定义？

给定行号和相应的文档内容，统计指定单词出现的位置

• Map函数：$<lineID,word>\to <word,lineID>$
• Reduce函数：$<word,lineID>\to <word,listoflineID>>$

3.4 矩阵乘法

问题定义？

两种算法：Map函数做什么？Reduce函数做什么？

1. 矩阵乘法1
   • Map：
     • ((A,i,j),aij)→(j,(A,i,aij))
     • ((B,j,k),bjk)→(j,(B,k,bjk))
   • Reduce：(j,(A,i,aij)),(j,(B,k,bjk))→((i,k),aij∗bjk)
   • Map：nothing（identity）
   • Reduce：((i,k),(v1,v2,…))→((i,k),∑vi)
2. 矩阵乘法2

   • Map函数：

     • ((A,i,j),aij)→((i,x),(A,j,aij)) for all x∈[1,n]
     • ((B,j,k),bjk)→((y,k),(B,j,bjk)) for all y∈[1,m]

   • Reduce函数：((i,k),(A,j,aij))∧((i,k),(B,j,bjk))→((i,k),∑aij∗bjk)

3.5 排序算法

Map函数做什么？Reduce函数做什么？解决问题的一个关键？

使用p台处理器，输入$<i,A[i]>$

• Map：$<i,A[i]>\to <j,((i,A[i]),y)>$

  1. 输出$<i\%p,((i,A[i]),0)>$

  2. 以概率T/n为所有$j\in [0,p-1]$输出$<j,((i,A[i]),1)>$

     否则输出$<j,((i,A[i]),0)>$

• Reduce：

  • 将y=1的数据收集为S并排序
  • 构造$(s_1,s_2,...,s_{p-1})$，$s_k$为S中第$k\lceil \frac{|S|}{p}\rceil$
  • 将y=0的数据收集为D
  • 对任意(i,x)∈D满足$s_k<x\le s_{k+1}$，输出<k,(i,x)>

• Map：nothing（identity）

• Reduce：$ <j, ((i, A[i]), . . . )>$

  • 将所有$(i,A[i])$根据$ A[i]$排序并输出

3.6 计算最小支撑树（生成树）

主要思想？Map函数做什么？Reduce函数做什么？

利用图划分算法，将图G划分成k个子图，在每个子图中计算最小生成树

算法的本质就是先在局部算好生成树，然后用剩余的连接这些生成树的边组成一个新的图，并求出这个新的图的最小生成树作为最总的结果

• Map：input:<(u,v),NULL>
  • 转化<(h(u),h(v));(u,v)>
  • 针对上述转化数据，如果h(u)=h(v)，则对所有 j∈[1,k]，输出<(h(u),j);(u,v)>
• Reduce：input:<(i,j);Eij>
  • 令Mij=MSF(Gij)
  • 对Mij中的每条边e=(u,v)输出<NULL;(u,v)>
• Map：nothing（identity）
• Reduce：M=MST(H)

4 外存模型算法

4.1 外存模型

在I/O模型中，内存的大小为___，页面大小为___，外存大小___。连续读取外存上的N个数据，需要多少次I/O？

M，B，无限，N/B

4.2 计算矩阵乘法

输入两个大小为N×N的矩阵X和Y

1. 将矩阵分为大小为___的块
2. 考虑X×Y矩阵中的每个块，显然共有___个块需要输出
3. 每个块需要扫描___对输入块
4. 每次内存计算需要___次I/O
5. 共计___次I/O

$\sqrt{M}/2\times \sqrt{M}/2$

$O((\frac{N}{\sqrt{M}}{)}^2)$

$\frac{N}{\sqrt{M}}$

O(M/B)

$O((\frac{N}{\sqrt{M}}{)}^3\cdot M/B)$

4.3 数据结构

4.3.1 外存栈

内存维护大小为___的数组，实现内存栈结构，外存中存储其余数据

怎么压栈（push）?
怎么弹栈（pop）？

I/O代价分析：
▷ 最坏情况代价：O(1)次I/O
▷ 均摊代价（amortized analysis）：___，最优

2B

没满就压，满了就外写后压

不空就弹，空了就读了再弹

O(1/B)

4.3.2 外存链表

队列（Queue）
▷ 内存维护2个大小为B的数组A和B，一个用于出队，一个用于入队
▷ A和B中分别存储?
▷ 外存中存储其余数据
如何处理队列操作？
▷ 入队（insert）?
▷ 出队（remove）?
I/O代价分析：
▷ 最坏情况代价：O(1)次I/O
▷ 均摊代价（amortized analysis）：___，最优

k个队头数据和k′个队尾数据

B没满就入内存，满了就外写后再入内存

A没空就弹，空了就读了再弹

O(1/B)

4.3.3 链表

进行三种操作：insert(x,p),remove§,traverse(p,k)

• 想法二：块“半满”⇒数据至少B/2；

  在外存模型下，将一个链表中连续的元素放在一个大小为B的块中。同时，令每个块大小至少为B/2：
  ▷ remove: 什么情况下合并？什么情况下均分?
  ▷ insert: 什么情况下均分?
  ▷ traverse: ___，insert和remove最坏情况代价为O(1)

  ▷ 均摊代价：N次连续插入___，连续删除___

  小于B/2，则与邻居块合并，合并后大于B则均分

  大于B，平均划分

  O(2k/B)

  N次连续插入O(2N/B)，连续删除$O(lo{g}_{2}B\cdot N/B)$

• 想法三：连续的两个块至少包含2B/3个数据；

  连续的两个块至少包含2B/3个数据；内存维护大小为B缓冲区
  ▷ remove: 什么情况下合并？什么情况下均分？
  ▷ insert: 什么情况下合并？什么情况下均分?
  ▷ traverse: ___

  ▷ 均摊代价：N次连续插入___，连续删除___
  ▷ 均摊代价：N次连续更新___

删除并检查是否有相邻块使得数据量 ≤ 2B/3，有则合并

若当前块满，向邻居插入；邻居均满，均分当前块

O(3k/B)

O(2N/B)，O(3N/B)

O(12N/B)

4.4 搜索结构

进行三种操作：insert(x),remove(x),query(x)

$(a,b)-tree:$ a与b的关系

类似二分查找树$\Rightarrow (p_0,k_1,p_1,k_2,p_2,...,k_c,p_c)$

root节点有__个孩子；每个非叶子节点的孩子数目__：

• remove：怎么操作?
• insert：怎么操作?
• query：时间复杂度？

2 ≤ a ≤ (b + 1)/2

根节点有0或≥ 2个孩子，其它非叶子节点的孩子数目∈ [a, b]

删除后若小于a，与邻接块合并，合并后若大于b，平均划分

插入后若大于b，均分

$ O(log_a(N/a))$

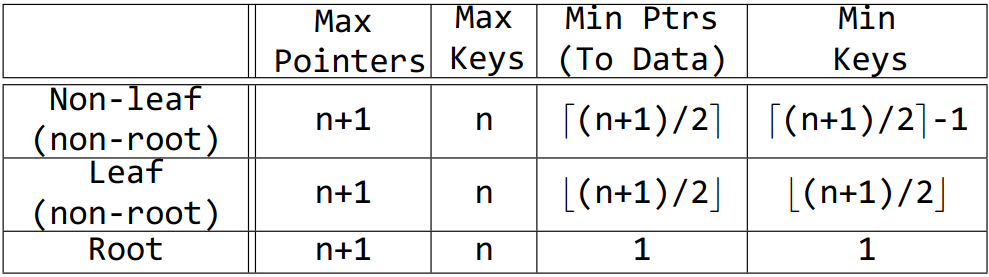
插入操作

假设插入的键值为K，首先找到对应的叶结点L

• 如果L中有空闲空间，那么直接插入，结束；

• 否则将叶结点分裂为两个结点，并且把其中的键分到这两个新结点中，使得键个数满足最小要求；

  • 当分裂叶结点N时：

    ▷创建一个新结点M，让M为N的右侧兄弟，将键排序，前$\lceil (n+1)/2\rceil$个留在N中，其他键‐指针放入M中。

  • 当分裂非叶结点N时：
    ▷将键‐指针排序，前$\lceil (n+2)/2\rceil$个指针留在N中，剩下的$\lfloor (n+2)/2\rfloor$个指针放入M中。
    ▷前$\lceil n/2\rceil$个键留在N中，后$\lfloor n/2\rfloor$个键放入M中，中间那个键留出来，插入到上一层结点中，该键指针指向M。

删除操作

假设删除的键值为K，首先找到对应的叶结点L。

• 如果L中删除K后仍然具有满足最小要求的键个数，停止

• 否则需要做如下处理：

  ▷尝试与L的相邻兄弟节点之一合并（合并后仍能放入同一节点），合并后，相当于在上层结点删除了一个键值，那么递归处理；

  ▷否则，考虑L的相邻兄弟

  • 假设其中一个能够提供L一个键‐指针，并且去除该键‐指针后该兄弟结点仍然满足键数的最小要求，那么L从该兄弟处借得一对键‐指针，并更新父节点的对应键值；
  • 如果两个兄弟都无法提供一个键‐指针，那么必然是如下情况：L的键数少于最小数，L兄弟M的键数恰好为最小数，那么两个结点可以合并。

B+树–性能

结点中指针数目的最大值：n，记录条数：N
B+Tree的插入操作：$O(lo{g}_{\lceil n/2\rceil }(N))$
B+Tree的删除操作：$O(lo{g}_{\lceil n/2\rceil }(N))$

4.5 外存排序

▷ 给定__个数据
▷ 分成大小为__的组，每组可在内存排序，需要__次I/O
▷ 排好序的分组，进行归并（Merge）
▷ 每次可以归并__个分组
▷ I/O代价：
▷ 画图理解

N

O(M)，O(M/B)

O(M/B)

$O(N/B\cdot lo{g}_{M/B}\frac{N}{B})$或$O(N/B\cdot lo{g}_{M/B}\frac{N}{M})$（存疑）

4.6 List Ranking

问题定义？（两个问题）

算法？（四个步骤）

给定大小为N的邻接链表L，L存储在数组（连续的外存空间）中，计算每个节点的rank（在链表中的序号）

输入大小为N的外存链表L

1. 寻找L中的一个顶点独立集 X
2. 将X中的节点“跳过”，构建新的、更小的外存链表L′
3. 递归地求解L′
4. 将X中的节点“回填”，根据L′的rank构建L的rank