1,引文
原文教程为川川菜鸟的《打卡第五天—图的最短路径和距离》
链接为第三天打卡--非线性规划(1)_python菜鸟-CSDN博客打卡第五天—图的最短路径和距离_python菜鸟-CSDN博客第三天打卡--非线性规划(1)_python菜鸟-CSDN博客
有需要者自取。
相比于前面咱们所学的特殊算法(线性规划),今天我们学的是另一类方法——动态规划。作为考察问题的一种途径,它不像线性规划有一个明确的解题模板步骤,而是需要我们具体问题具体分析。
因此,在学习时,除了要对基本概念和方法正确理解外,应以丰富的想象力去建立模型,用创造性的技巧去求解。
二,教程
1,sparse创建稀疏矩阵
假如,我们有这样的无向图(图中的数字代表两点的距离)
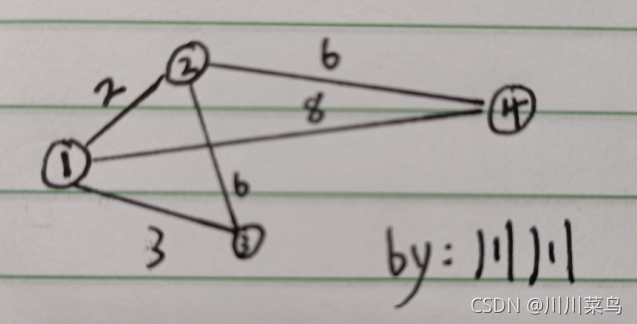
我们可以这样写代码
%w(起点,终点)=权重值
clear all
clc
w=zeros(4);
w(1,2)=2;w(1,3)=3;w(1,4)=8;
w(2,3)=6;w(2,4)=6;
G=sparse(w)
运行得到结果

或者,咱们也可以这样写
clear all
clc
%sparse([起点集合],[对应终点集合],[对应权重集合])
G = sparse([1 1 1 2 2],[2 3 4 3 4],[2 3 8 6 6]);
s=sparse(G)
结果同样为

2,有向图最短路径
在这里,我们要提到一个新的函数: graphallshortestpaths
语法如下

然后,咱们创建一个有向图,来作为咱们接下来讲解的背景
clear all
clc
G = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 29 21])
view(biograph(G,[],'ShowWeights','on'))


然后呢,咱们在代码里再加个那么一行。
clear all
clc
G = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 29 21])
view(biograph(G,[],'ShowWeights','on'))
graphallshortestpaths(G)

咱们现在比之前多了什么?多了个ans。
那么这个是什么含义呢?
比方说,我们现在想从节点一,有方向的去往节点六的最短路径,就是95(第一行第六列)。那么,看第一行第一列的数字,为啥是0?从节点一走到节点一,距离可不就是0嘛。
所以,咱们得出一个通性。第一行是节点一到各个节点的最短距离。第二行是节点二到各个节点的距离。以此类推。
那么,我们现在知道了某个点到某个点的最短距离,是不是可以求出这个距离所对应的路径呢?
其实,不难看出:21+32+38=95
路径便是1-5-3-6
参考
如果觉得自己没那么轻易看出来,不用灰心,咱们接着往下看
3,有向图最短路径(2)
在这里,咱们需要一位新朋友:函数dijkstra.m(你不需要修改,知道这个函数具体意思,我们调用它就行)
看代码
function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
if i~=start
label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)<n
for i=1:n
ins=0;
for j=1:length(s)
if i==s(j)
ins=1;
end
end
if ins==0
v=i;
if label(v)>(label(u)+w(u,v))
label(v)=(label(u)+w(u,v));
f(v)=u;
end
end
end
v1=0;
k=inf;
for i=1:n
ins=0;
for j=1:length(s)
if i==s(j)
ins=1;
end
end
if ins==0
v=i;
if k>label(v)
k=label(v); v1=v;
end
end
end
s(length(s)+1)=v1;
u=v1;
end
min=label(terminal); path(1)=terminal;
i=1;
while path(i)~=start
path(i+1)=f(path(i));
i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);
这时候,我们去解决上述问题
% 构造邻接矩阵
a = zeros(6);
a = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 29 21])
a = a + a';
a(a==0) = inf; % 零元素换成inf
a(eye(6,6)==1)=0; % 对角线换成 0
view(biograph(a,[],'ShowWeights','on'))
[min,path]=dijkstra(a,1,6) % dijkstra模型求解节点一到节点六最短路径


所以,最短路径就是82,路径为1-5-3-6。
4,无向图最短路径
无向,其实把两个有向结合起来就行。比如,我要看1和6的无向最短路径,我可以先看1到6最短路径,再看6到1最短路径即可。