基于贪心策略优化的拉丁超立方设计

一. 内容简介

基于贪心策略优化的拉丁超立方设计

二. 软件环境

2.1 matlab

三.主要流程

3.1 拉丁超立方设计

原理我就不讲了，我就讲结果什么的
代码

% 设置变量范围和样本数量
rangeX = [0 1]; % X 变量范围
rangeY = [0 1]; % Y 变量范围
numSamples = 500; % 样本数量

% 贪心策略生成优化的拉丁超立方设计
design = greedyOptimizationLHD(numSamples, 2, rangeX, rangeY);

% 绘制二维图
scatter(design(:,1), design(:,2), 'filled');
xlabel('X');
ylabel('Y');
title('Optimized Latin Hypercube Design using Greedy Optimization');

function design = greedyOptimizationLHD1(numSamples, numVariables, rangeX, rangeY)
    % 生成初始的拉丁超立方设计
    design = lhsdesign(numSamples, numVariables);
end

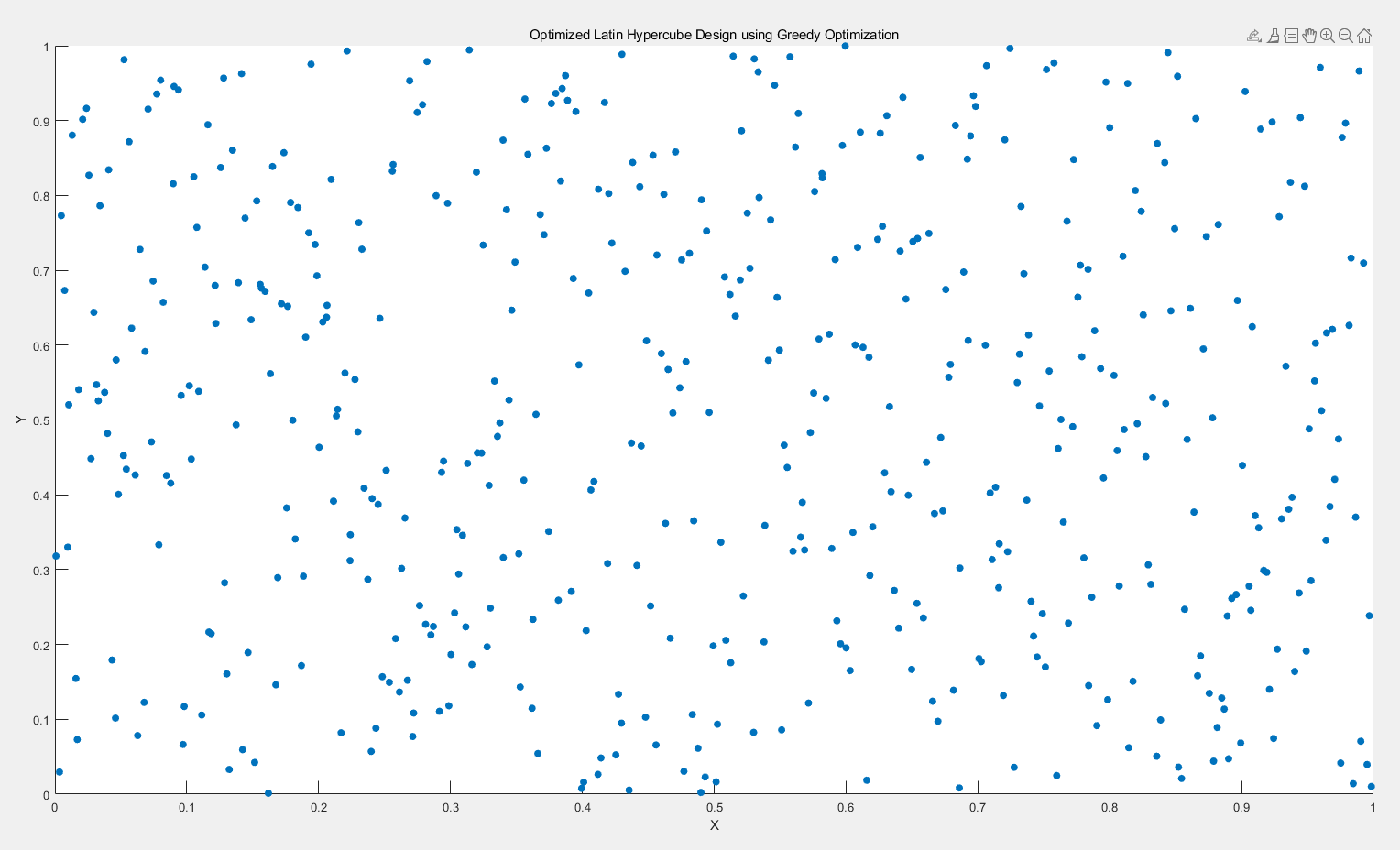
3.2 基于贪心策略优化的拉丁超立方设计(GPT)

整个代码一开始都是gpt写的，这是原代码，可以大致看一下，然后可以看他的问题，gpt生成的代码是有问题，

% 设置变量范围和样本数量
rangeX = [0 1]; % X 变量范围
rangeY = [0 1]; % Y 变量范围
numSamples = 20; % 样本数量

% 贪心策略生成优化的拉丁超立方设计
design = greedyOptimizationLHD(numSamples, 2, rangeX, rangeY);

% 绘制二维图
scatter(design(:,1), design(:,2), 'filled');
xlabel('X');
ylabel('Y');
title('Optimized Latin Hypercube Design using Greedy Optimization');

% 贪心策略生成优化的拉丁超立方设计函数
function design = greedyOptimizationLHD(numSamples, numVariables, rangeX, rangeY)
    % 生成初始的拉丁超立方设计
    design = lhsdesign(numSamples, numVariables);
    
    % 将设计映射到变量范围
    samplesX = design(:, 1) * (rangeX(2) - rangeX(1)) + rangeX(1);
    samplesY = design(:, 2) * (rangeY(2) - rangeY(1)) + rangeY(1);
    
    % 计算初始设计的适应度
    initialFitness = calculateFitness(samplesX, samplesY);
    
    % 迭代改进设计
    for iter = 1:100
        % 随机选择一个样本点
        index = randi(numSamples);
        
        % 随机生成新的样本点
        newX = rand * (rangeX(2) - rangeX(1)) + rangeX(1);
        newY = rand * (rangeY(2) - rangeY(1)) + rangeY(1);
        
        % 替换选中的样本点
        samplesX(index) = newX;
        samplesY(index) = newY;
        
        % 计算新设计的适应度
        newFitness = calculateFitness(samplesX, samplesY);
        
        % 如果新设计的适应度更好，则接受新设计
        if newFitness > initialFitness
            initialFitness = newFitness;
        else
            % 恢复原来的样本点
            samplesX(index) = design(index, 1) * (rangeX(2) - rangeX(1)) + rangeX(1);
            samplesY(index) = design(index, 2) * (rangeY(2) - rangeY(1)) + rangeY(1);
        end
    end
    % 更新最终的设计
    design(:, 1) = (samplesX - rangeX(1)) / (rangeX(2) - rangeX(1));
    design(:, 2) = (samplesY - rangeY(1)) / (rangeY(2) - rangeY(1));
end

% 计算设计的适应度
function fitness = calculateFitness(samplesX, samplesY)
    % 计算设计的适应度（距离的总和的倒数）
    distances = pdist([samplesX, samplesY]);
    fitness = 1 / sum(distances);
end

最前边这个设计映射到变量范围，其实不应该存在的，因为适应度里面是要求点的距离的，如果给入的变量一个范围特别大，一个变量范围特别小的话，根据距离来优化的时候，结果反而不如最开始的拉丁超立方设计了。

    % 将设计映射到变量范围
    samplesX = design(:, 1) * (rangeX(2) - rangeX(1)) + rangeX(1);
    samplesY = design(:, 2) * (rangeY(2) - rangeY(1)) + rangeY(1);

改成这样就行了，相当于归一化，保证每个范围都在0-1。归一化优点，我把gpt写的粘上来
使用归一化的设计结果有以下优点：

统一尺度：归一化可以消除不同维度之间的尺度差异，确保它们具有相对一致的范围。这样，您可以更方便地比较和权衡不同维度之间的影响。
可复用性：归一化的设计结果可以更容易地与其他模型、算法或方法集成。您可以使用相同的归一化范围将设计输入到其他模型中，而无需进行额外的缩放操作。
易解释性：归一化的设计结果更易于理解和解释，因为它们处于统一的范围内。您可以直接使用归一化的值，而不必考虑每个维度的实际范围。
因此，如果您的问题涉及到多个维度，并且这些维度具有不同的范围，我建议使用归一化的设计结果。这样可以更好地处理不同维度之间的尺度差异，并更方便地进行后续分析和应用。

    % 设计映射
    samplesX = design(:, 1);
    samplesY = design(:, 2);

第二个问题是，再点迭代过程里面，你会发现遇到不好的点的时候，design是一开始生成的点，也就是说他遇到不好的点的时候，都会退到最开始的点，就导致这个点迭代其实都没怎么进行，因为很容易就回到初始版本了，又从头开始了。

        % 如果新设计的适应度更好，则接受新设计
        if newFitness > initialFitness
            initialFitness = newFitness;
        else
            % 恢复原来的样本点
            samplesX(index) = design(index, 1) * (rangeX(2) - rangeX(1)) + rangeX(1);
            samplesY(index) = design(index, 2) * (rangeY(2) - rangeY(1)) + rangeY(1);
        end

这块基本就算输出了，他输出还是0-1,其实不是我们要的范围的

    % 更新最终的设计
    design(:, 1) = (samplesX - rangeX(1)) / (rangeX(2) - rangeX(1));
    design(:, 2) = (samplesY - rangeY(1)) / (rangeY(2) - rangeY(1));

还有最后这个适应度函数，我测试了几种,先看GPT给的，pdist 函数可以计算每个点与其他所有点之间的距离。如果有abcd四个点，距离求的就是,ab,bc,cd,da,ac,bd,

function fitness = calculateFitness(samplesX, samplesY)
    % 计算设计的适应度（距离的总和的倒数）
    distances = pdist([samplesX, samplesY]);
    fitness = 1 / sum(distances);
end

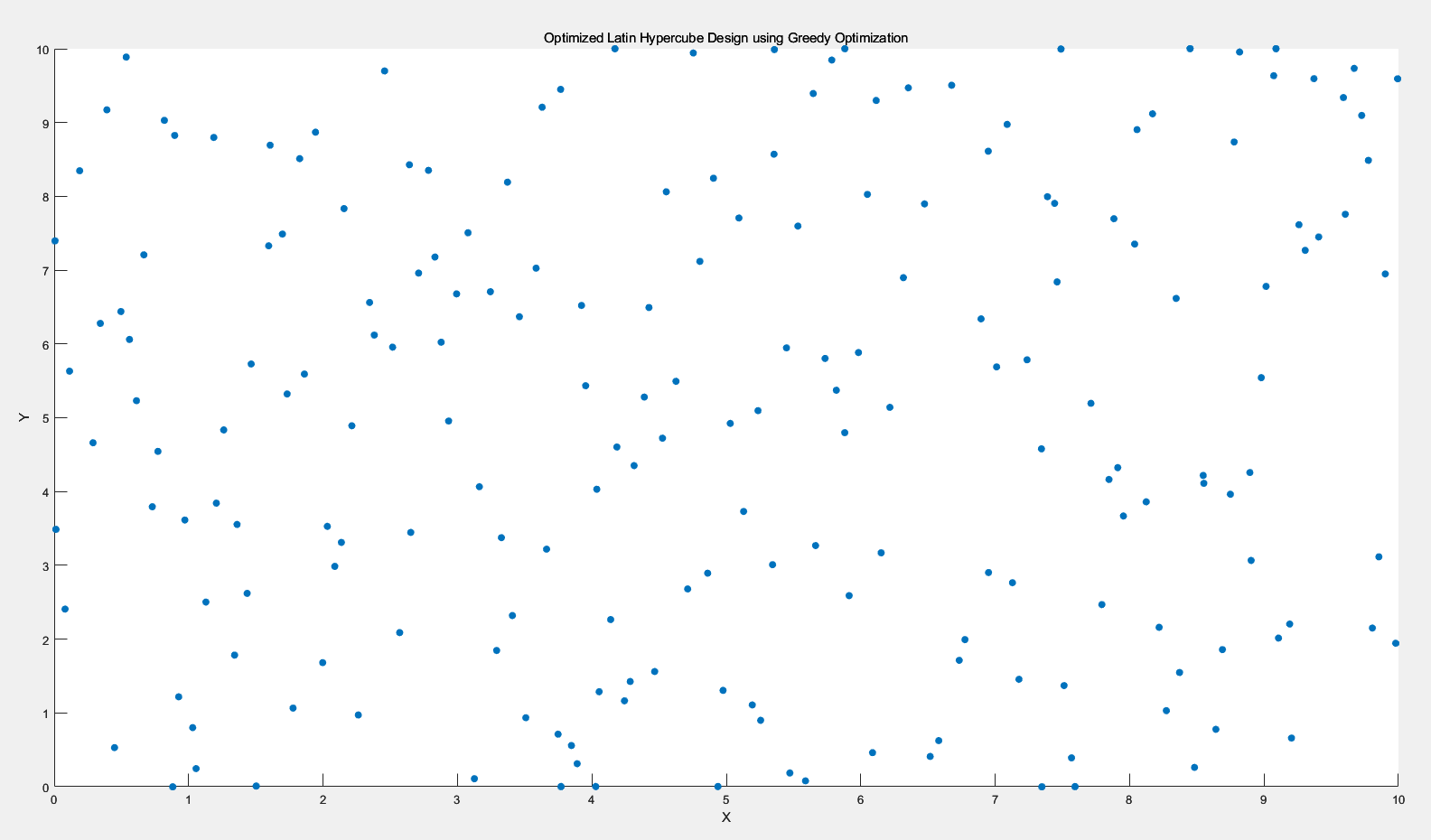
可以发现图已经很离谱了，聚集的很厉害

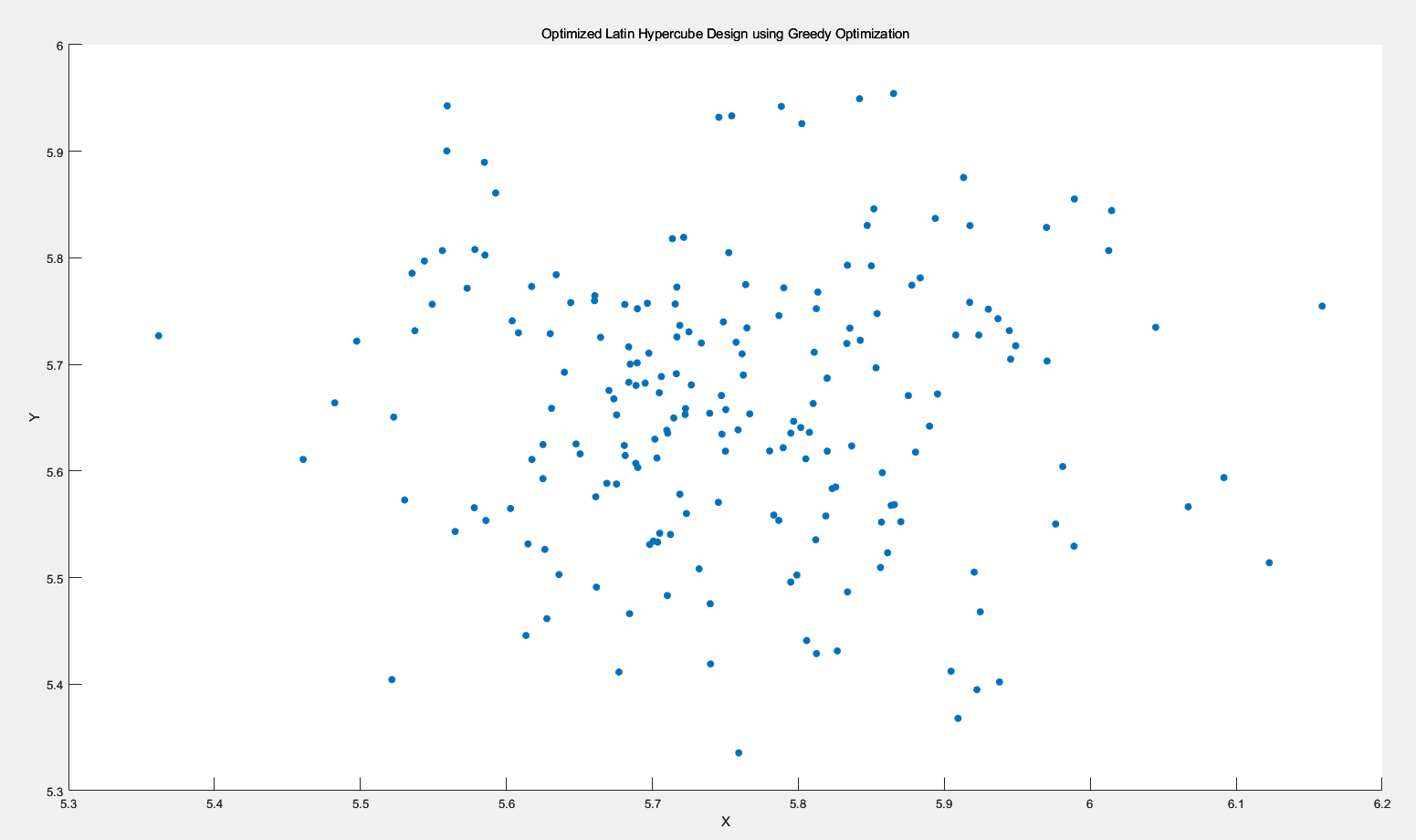
那么我把那个倒数给去一下，也是没办法用的

function fitness = calculateFitness(samplesX, samplesY)
    % 计算设计的适应度（距离的总和的倒数）
    distances = pdist([samplesX, samplesY]);
    fitness = sum(distances);
end

gpt又给的，效果也是一般，

% 计算设计的适应度
function fitness = calculateFitness(samplesX, samplesY)
    % 计算样本点之间的距离矩阵
    distances = pdist([samplesX, samplesY]);
    % 计算最小距离
    minDistance = min(distances);
    % 适应度为最小距离的倒数
    fitness = 1 / minDistance;
end

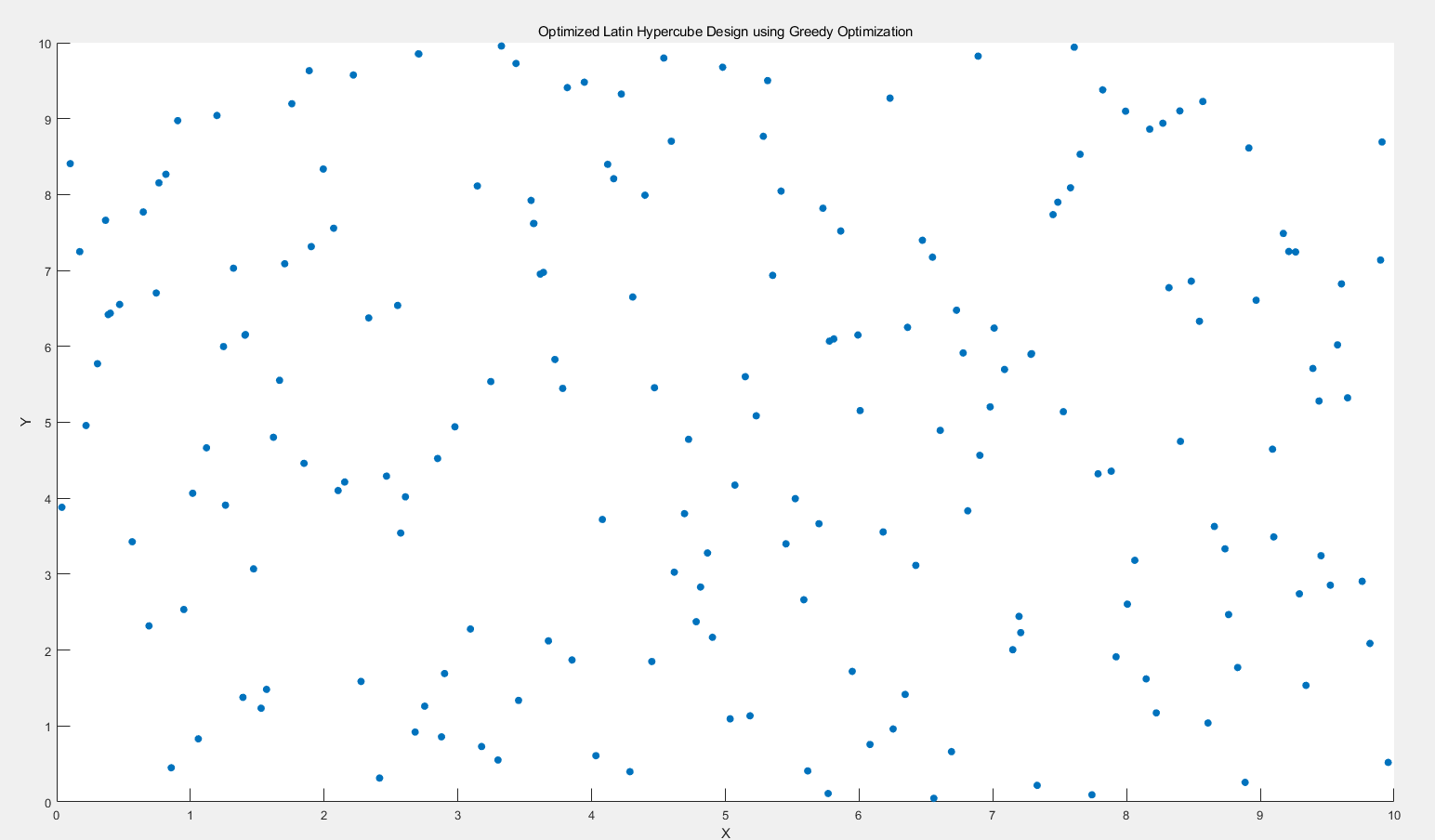
但是反过来呢，均匀的一批。

% 计算设计的适应度
function fitness = calculateFitness(samplesX, samplesY)
    % 计算样本点之间的距离矩阵
    distances = pdist([samplesX, samplesY]);
    % 计算最小距离
    minDistance = min(distances);
    % 适应度为最小距离的倒数
    fitness = minDistance;
end

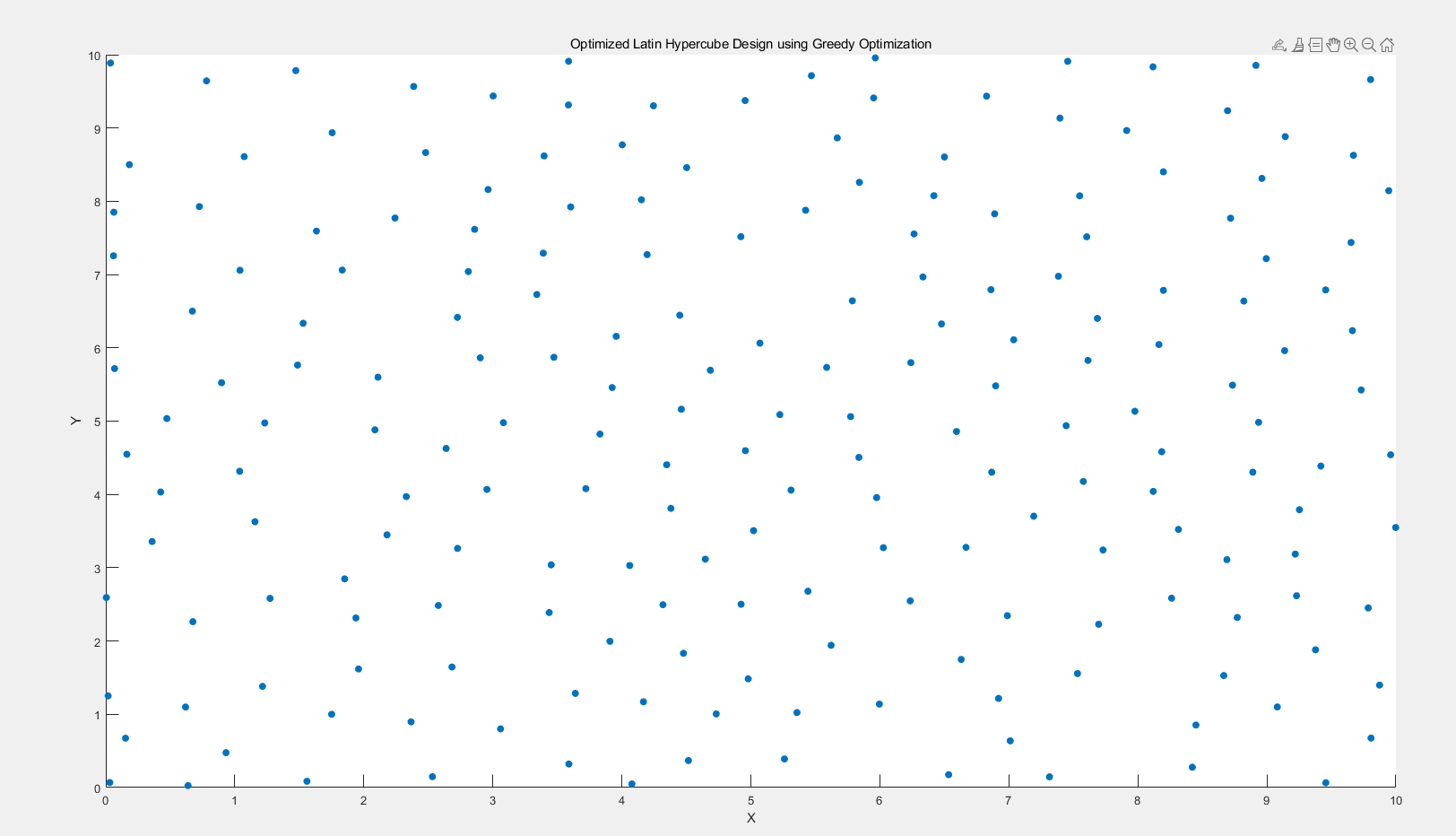
下面继续试试其他的，平均距离这个和前面那个距离总和一回事，就不放图了

% 计算设计的适应度（平均距离的倒数）
function fitness = calculateFitness(samplesX, samplesY, samplesZ, samplesW)
    % 计算样本点之间的距离矩阵
    distances = pdist([samplesX, samplesY, samplesZ, samplesW]);
    % 计算平均距离
    averageDistance = mean(distances);
    % 适应度为平均距离的倒数
    fitness = 1 / averageDistance;
end

还有一个是计算最大间距的倒数作为适应度值。

% 计算设计的适应度
function fitness = calculateFitness(samplesX, samplesY)
    maxDistanceX = max(pdist(samplesX));
    maxDistanceY = max(pdist(samplesY)); 
    % 计算最大间距的倒数作为适应度值
    fitness = 1 / max([maxDistanceX, maxDistanceY]);
end

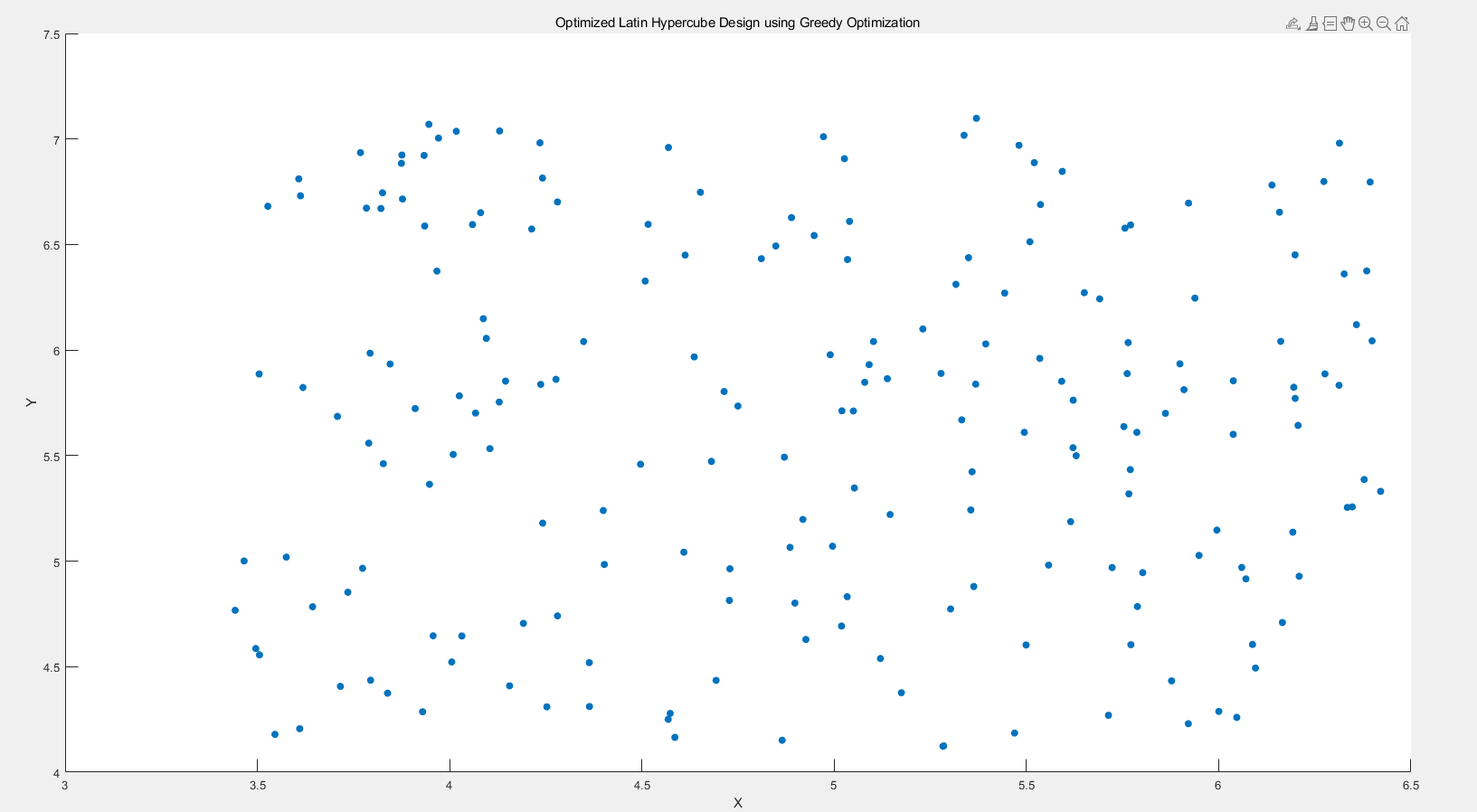
倒过来，其实也一般，会稍微好些，因为这个适应度这样计算的话，就相当于忽略了空间的一个分布的，所以优化没有那么好，他只是让个个变量在自己的维度更均匀了一些，但是全局而言，并没有好多少

3.3 基于贪心策略优化的拉丁超立方设计

放一些概念

欧氏距离（Euclidean distance）是在多维空间中计算两个点之间的直线距离的一种度量方法。在二维空间中，欧氏距离的计算公式为：
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
其中 (x1, y1) 和 (x2, y2) 分别表示两个点的坐标。在更高维空间中，欧氏距离的计算公式类似，通过计算每个维度上的差值的平方和再取平方根来得到两个点之间的距离。
在优化问题中，通过最大化或最小化最小欧氏距离，可以使得样本点之间的距离尽可能大或尽可能小，从而达到分散或聚集的效果。

上面那个最小距离的，gpt给的是最小距离的倒数，我特地找了一下东西

多孔质气体径向轴承静动特性研究论文里面提到了部分的优化方法，最大化最小的 Euclidean 距离（就是最大化最小的欧氏距离），也就是尽可能让每一个点离最近的一个点的距离要尽可能的大。

里面MATLAB中dist与pdist、pdist2的区别,可以看这个MATLAB中pdist、pdist2的区别与联系（http://t.csdn.cn/MkWO1）
简单理解就是，如果只有一个点集，pdis算的是当前这些点集的相互距离，如果有两个或多个距离，就用pdist2，他算的是和其他点集的项目相互距离

GPT之前也给写过这个，所以我觉着适应度，用这个是比较合理的

% 计算设计的适应度
function fitness = calculateFitness(samplesX, samplesY)
     % 计算样本点之间的距离矩阵
     distances = pdist([samplesX, samplesY]);
     % 计算最小距离
     minDistance = min(distances);
     % 适应度为最小距离的倒数
     fitness = minDistance;
end

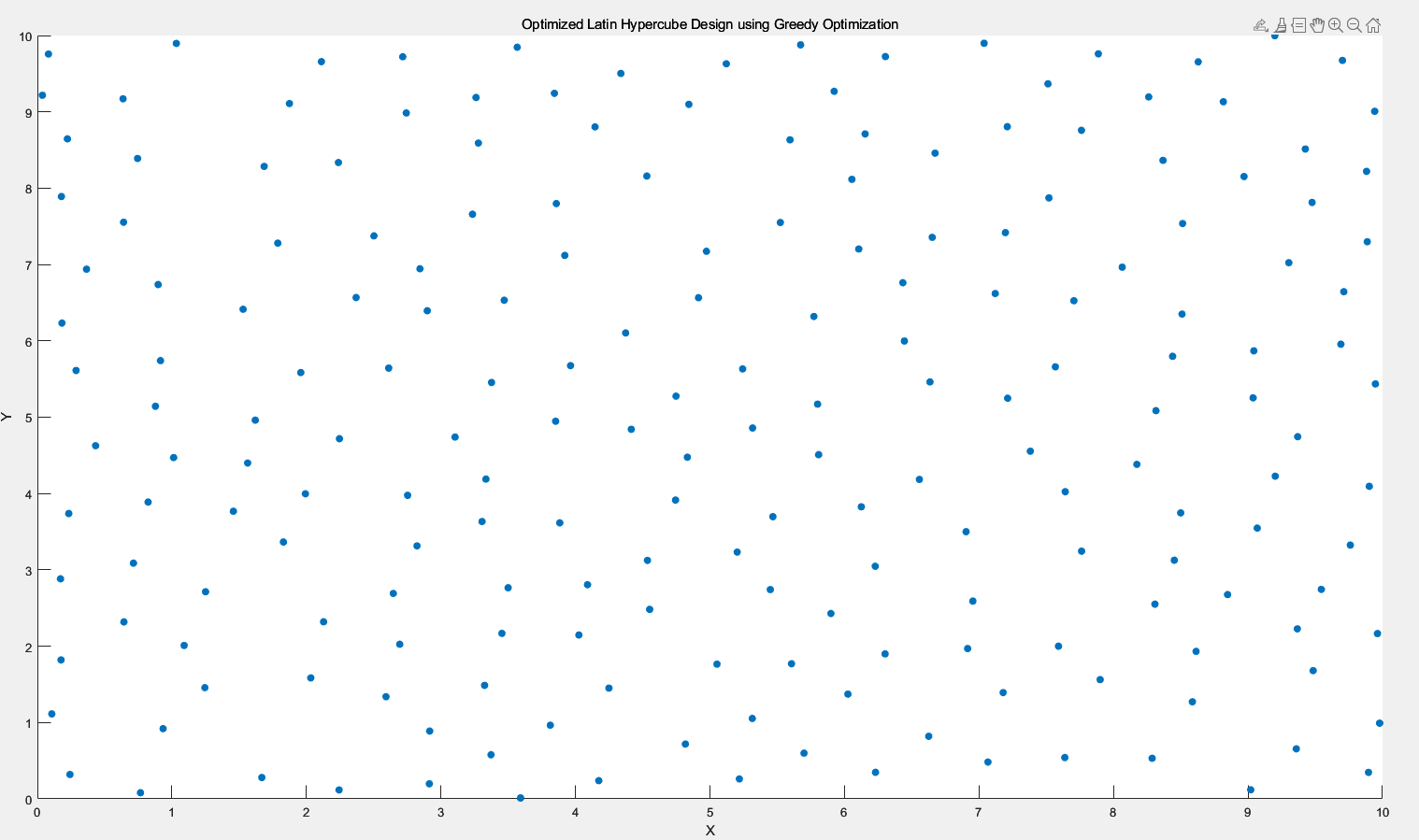
最大最小距离法（Maximum Minimum Distance）是一种优化方法，用于改进拉丁超立方设计。它的目标是最大化样本点之间的最小距离，以增加样本点之间的离散性和均匀性。

下面是最大最小距离法生成优化的基本思路：
1首先，生成一个初始的拉丁超立方设计。
2计算初始设计中样本点之间的最小距离。
3进行优化迭代，每次迭代都会生成一个新的设计并计算最小距离。
4在每次迭代中，对于每个样本点，通过随机重分配来生成一个新的位置。这可以通过交换两个样本点的位置或在样本点的范围内随机选择一个新的位置来实现。
5计算新设计中样本点之间的最小距离。
6如果新的设计的最小距离优于之前的设计，则接受该设计作为当前最优设计；否则，保留之前的设计。
重复步骤 4-6，直到达到指定的迭代次数或满足停止条件

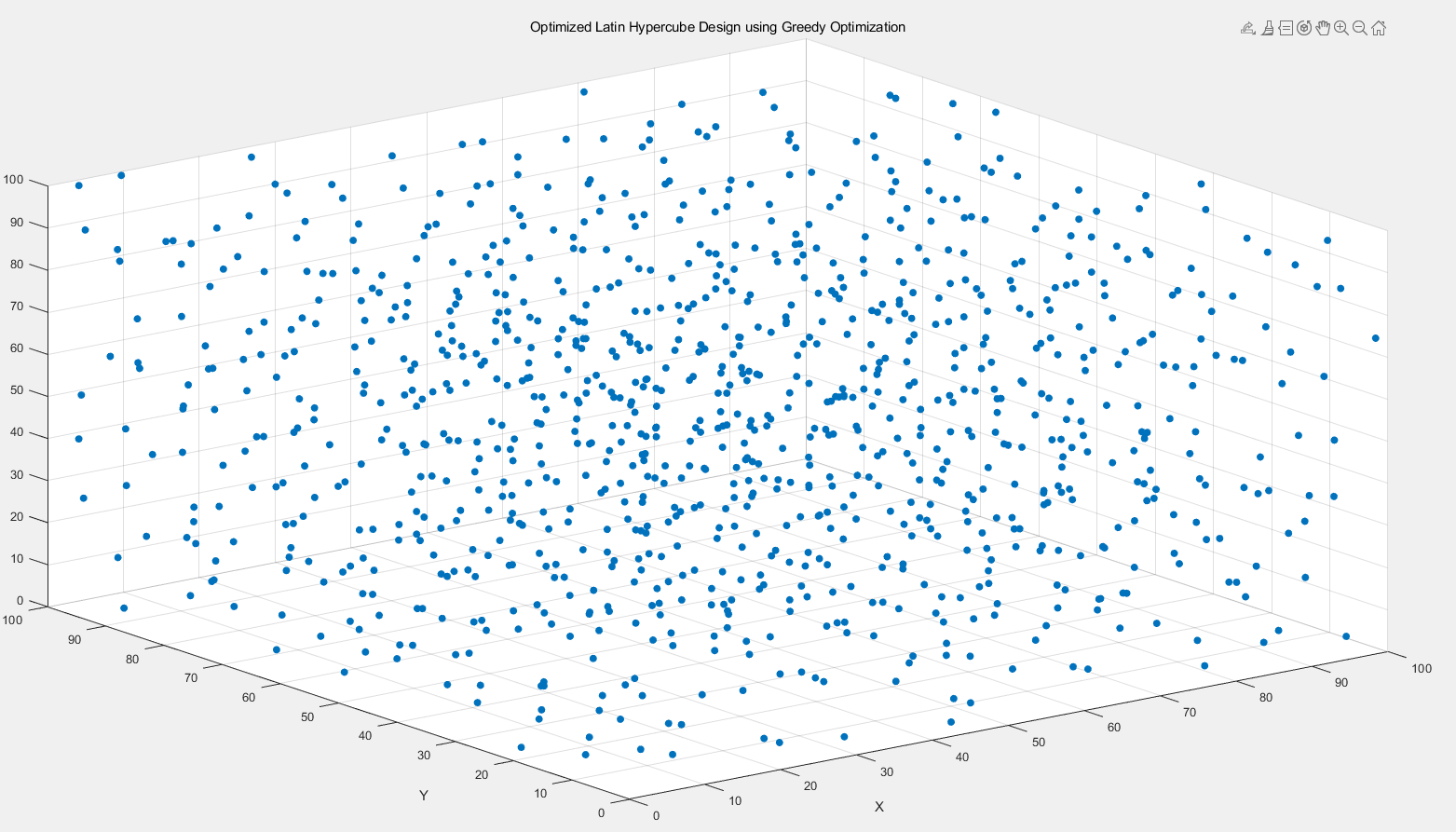
说下我的理解，我一开始认为这个靠距离优化的和拉丁超立方已经没有什么关系，因为他一直在用随机点替换，拉丁超立法只是提供了一个初始分布，这个分布一开始我认为随机的可能也是可以的。但是后来看着图想了想，理解的可能不太对，现在我觉着他这个优化，靠最小距离来的优化，一开始多维分布点是会有聚集的，而这个优化的思想应该是把相邻比较近的点用一个位置更好的点替换掉，也就是让邻近的点换一个比较空的位置，所以分布就会更均匀了。

全部代码

% 设置变量范围和样本数量
rangeX = [0 100]; % X 变量范围
rangeY = [0 100]; % Y 变量范围
numSamples = 1000; % 样本数量

% 贪心策略生成优化的拉丁超立方设计
design = greedyOptimizationLHD(numSamples, 2, rangeX, rangeY);

% 绘制二维图
scatter(design(:,1), design(:,2), 'filled');
xlabel('X');
ylabel('Y');
title('Optimized Latin Hypercube Design using Greedy Optimization');

% 贪心策略生成优化的拉丁超立方设计函数
function design = greedyOptimizationLHD(numSamples, numVariables, rangeX, rangeY)
    % 生成初始的拉丁超立方设计
    design = lhsdesign(numSamples, numVariables);
    
    % 设计映射
    samplesX = design(:, 1);
    samplesY = design(:, 2);
    
    % 计算初始设计的适应度
    initialFitness = calculateFitness(samplesX, samplesY);
    
    % 迭代改进设计
    for iter = 1:numSamples*10000
        % 随机选择一个样本点
        index = randi(numSamples);
        

        prevX = samplesX(index);
        prevY = samplesY(index);
        % 随机生成新的样本点
        newX = rand;
        newY = rand;
        
        % 替换选中的样本点
        samplesX(index) = newX;
        samplesY(index) = newY;
        
        % 计算新设计的适应度
        newFitness = calculateFitness(samplesX, samplesY);
        
        % 如果新设计的适应度更好，则接受新设计
        if newFitness > initialFitness
            initialFitness = newFitness;
        else
            samplesX(index) = prevX;
            samplesY(index) = prevY;
        end
    end
    

    % 将设计映射到变量范围
    samplesX = samplesX * (rangeX(2) - rangeX(1)) + rangeX(1);
    samplesY = samplesY * (rangeY(2) - rangeY(1)) + rangeY(1);
    % 更新最终的设计
    design(:, 1) = samplesX;
    design(:, 2) = samplesY;
end

% 贪心策略生成优化的拉丁超立方设计函数
function design = greedyOptimizationLHD1(numSamples, numVariables, rangeX, rangeY)
    % 生成初始的拉丁超立方设计
    design = lhsdesign(numSamples, numVariables);
end


% 计算设计的适应度
function fitness = calculateFitness(samplesX, samplesY)
     % 计算样本点之间的距离矩阵
     distances = pdist([samplesX, samplesY]);
     % 计算最小距离
     minDistance = min(distances);
     % 适应度为最小距离的倒数
     fitness = minDistance;
end

3.4 关于迭代次数的选取

3.4.1 一维情况下

普通拉丁超立方，可以看到点分布并不是很均匀的，会有靠很近的点，我说的迭代都是一个点迭代多少次，不是总的迭代多少次

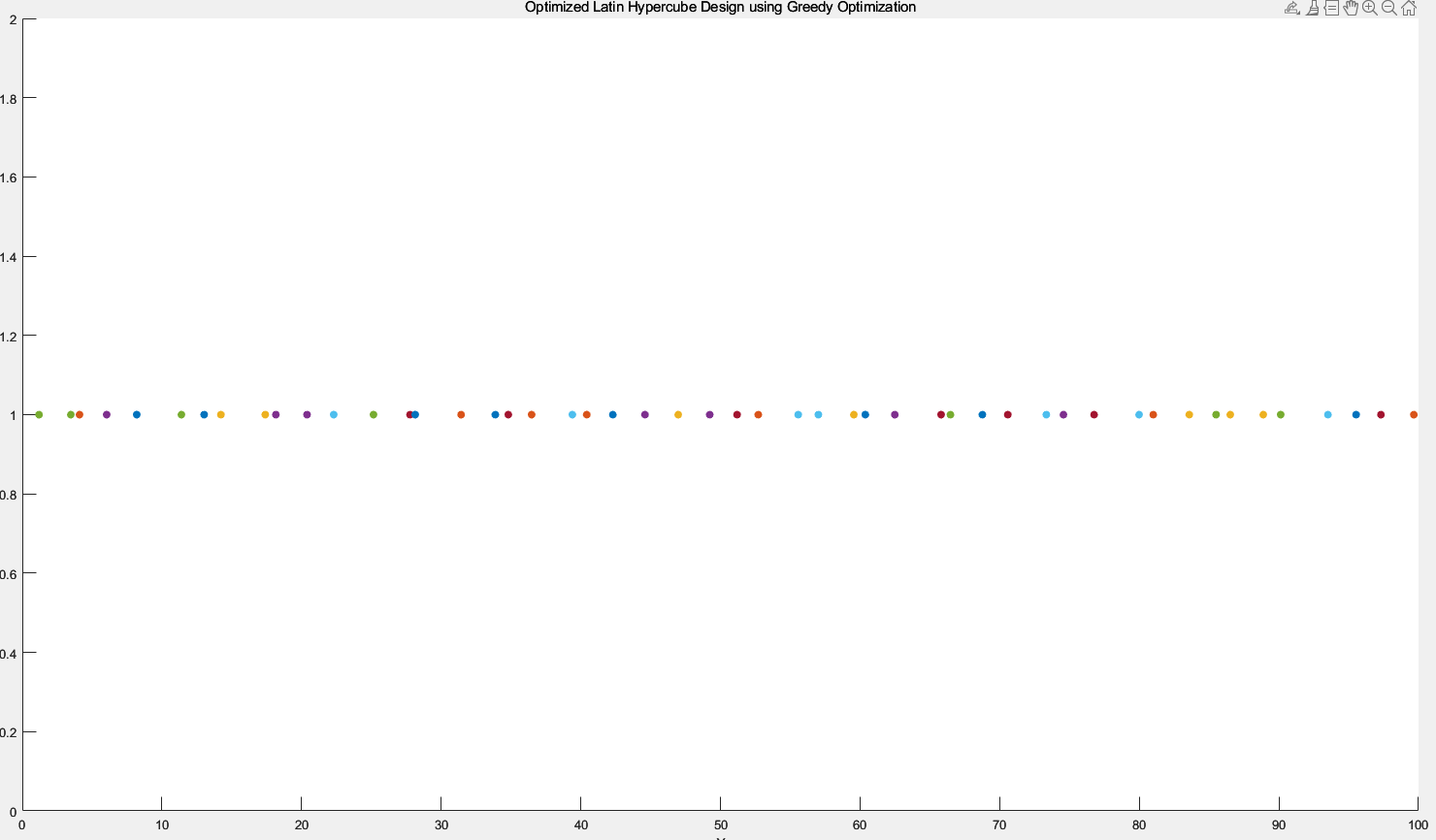
然后使用优化方法，一个点迭代10次

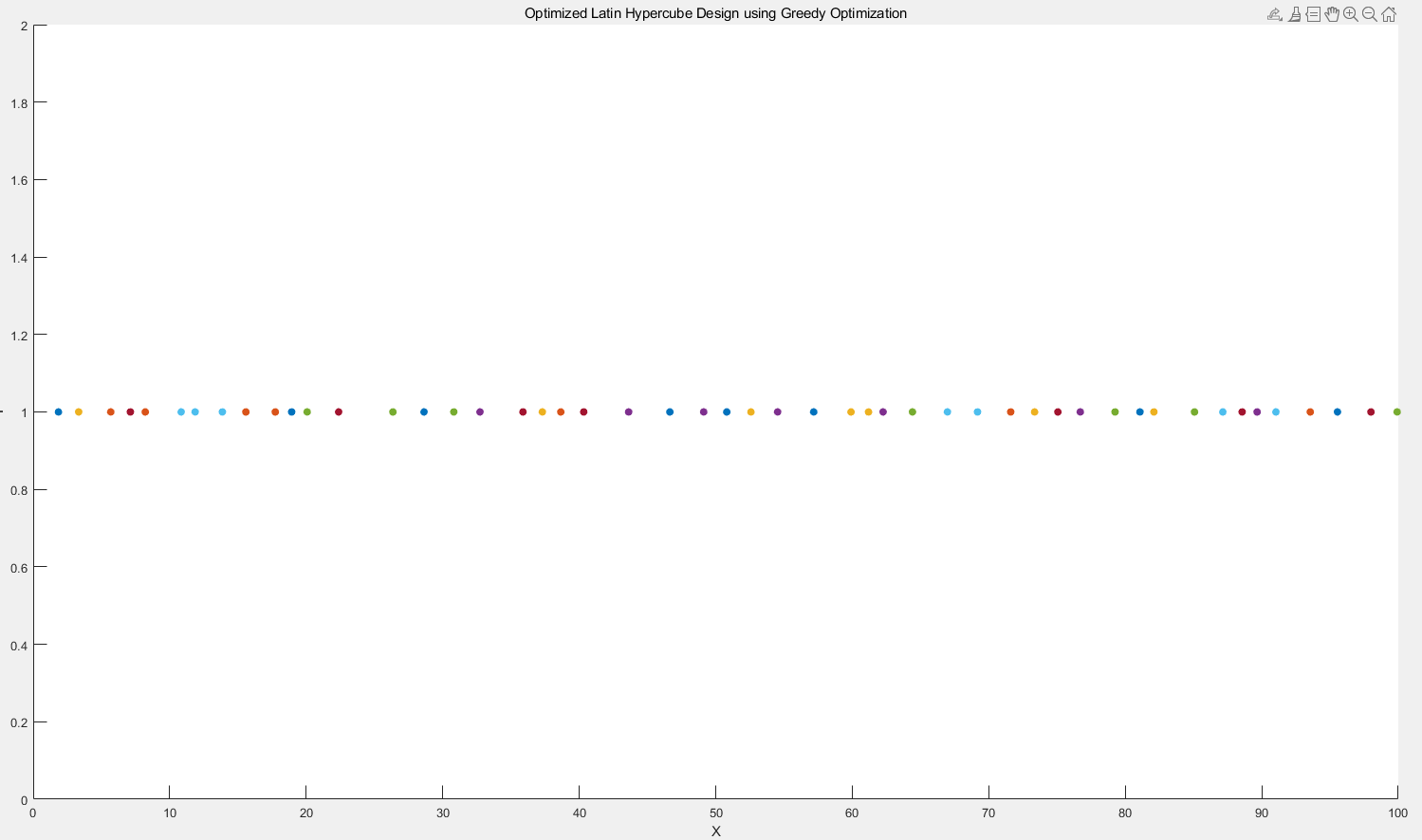
迭代100次

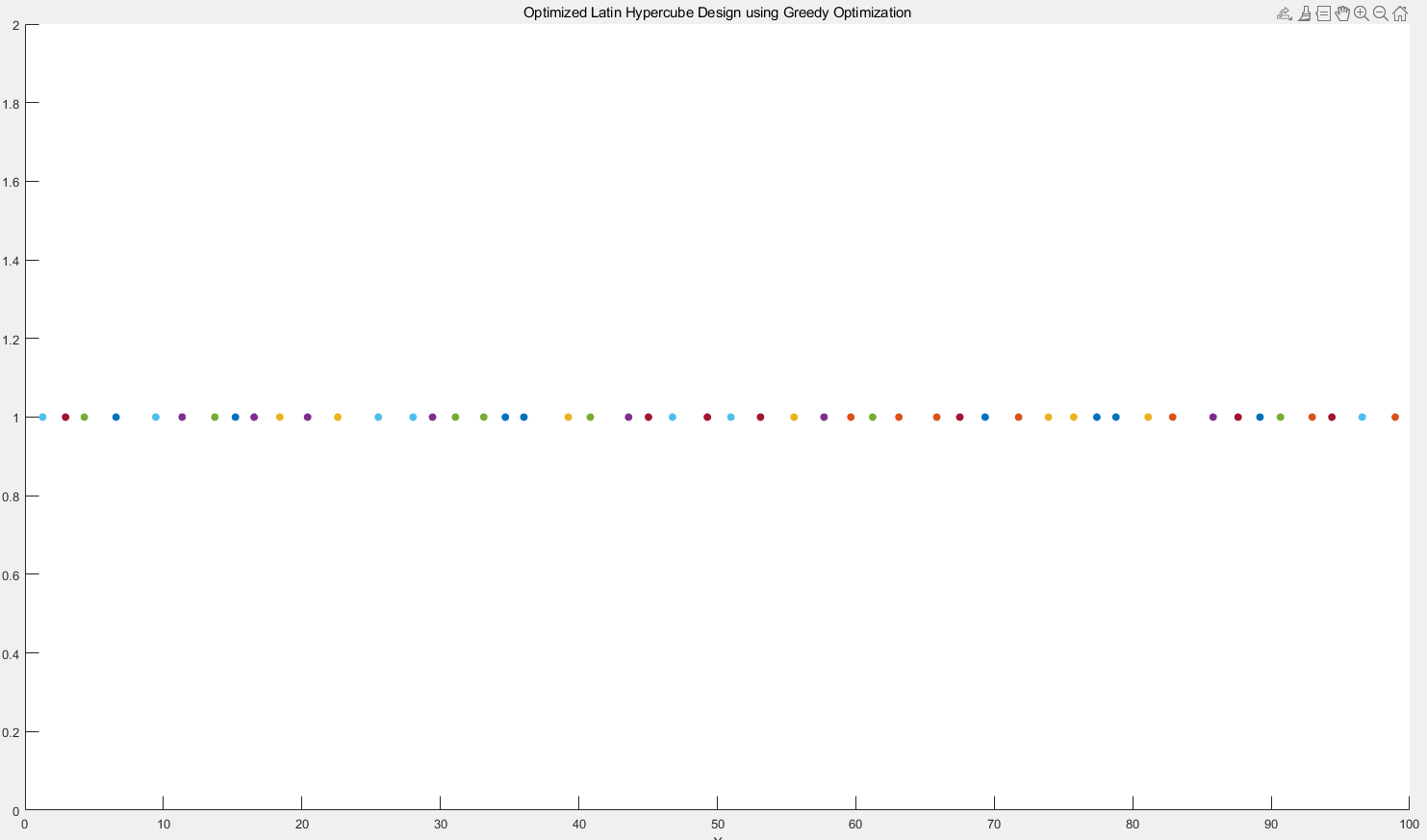
迭代1000次

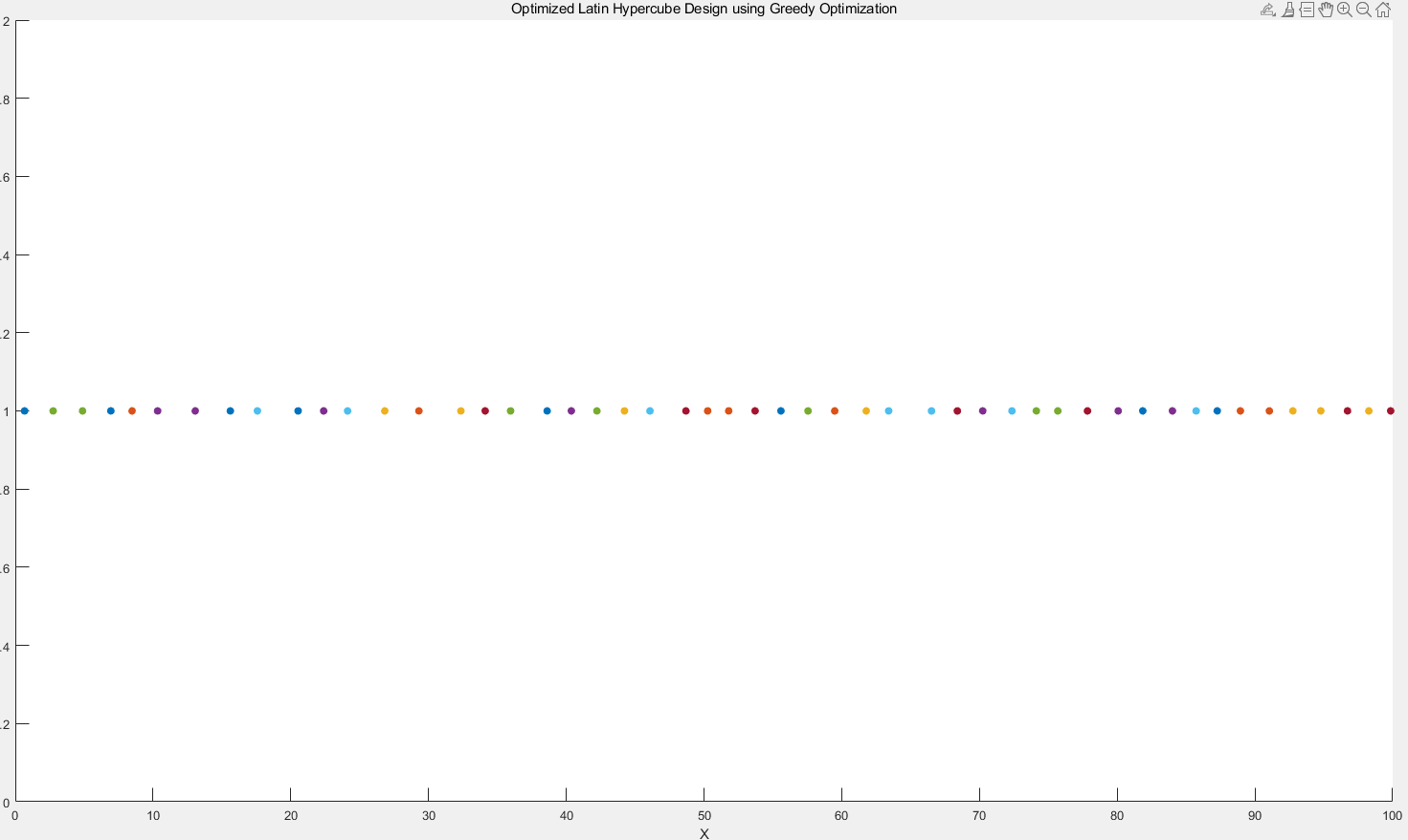
迭代10000次

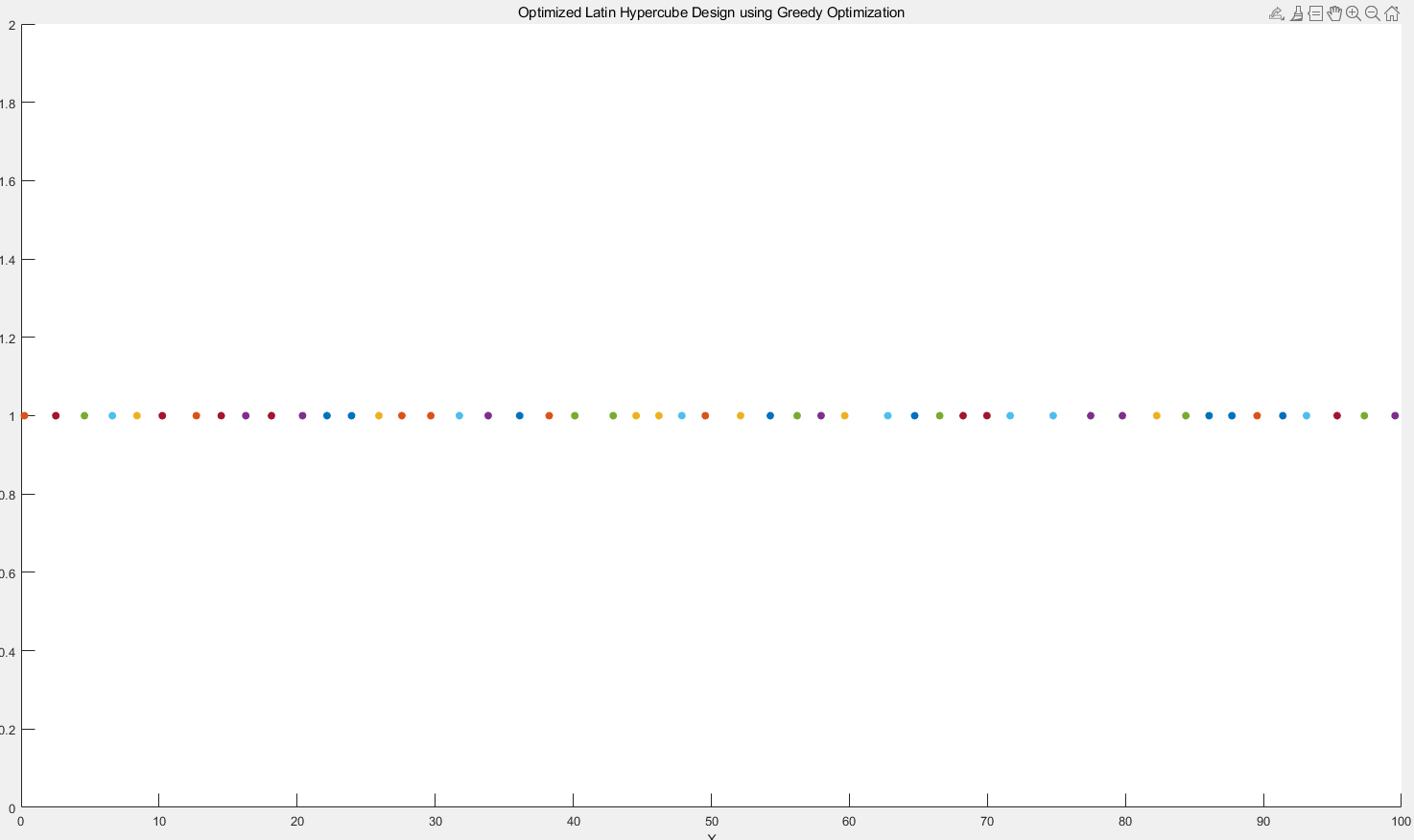
迭代100000次，巨均匀

3.4.2 二维情况下

不迭代优化

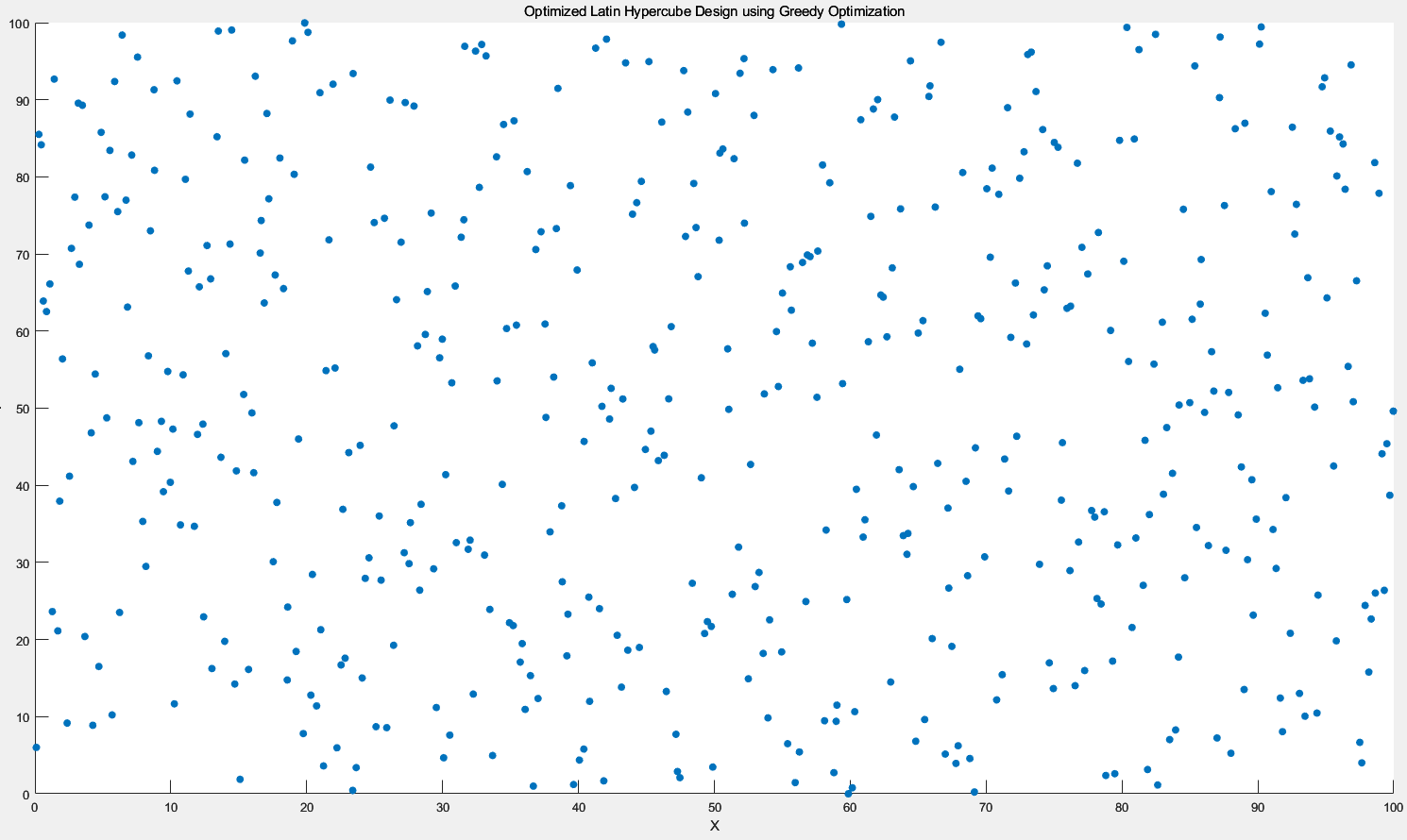
迭代10次

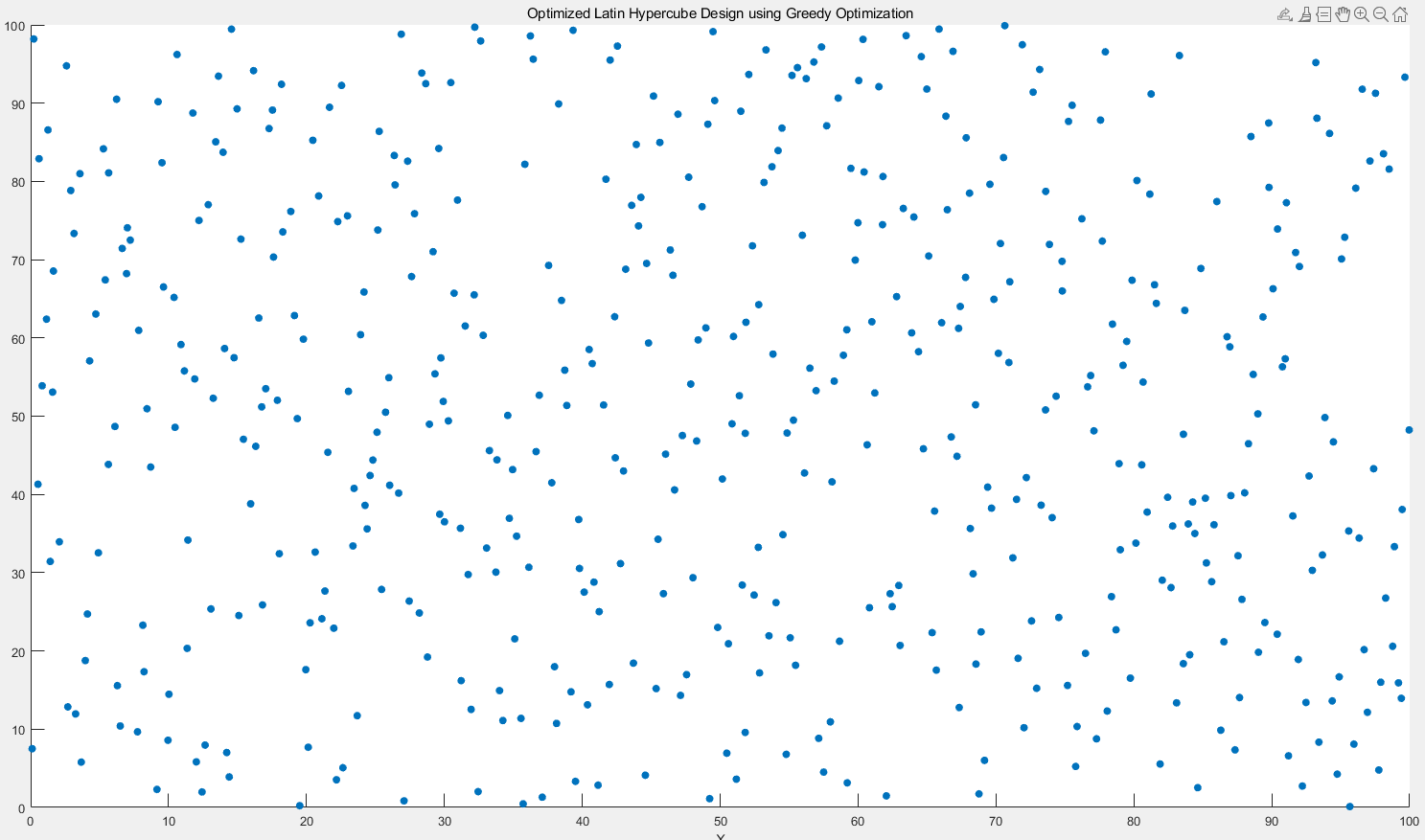
迭代100次

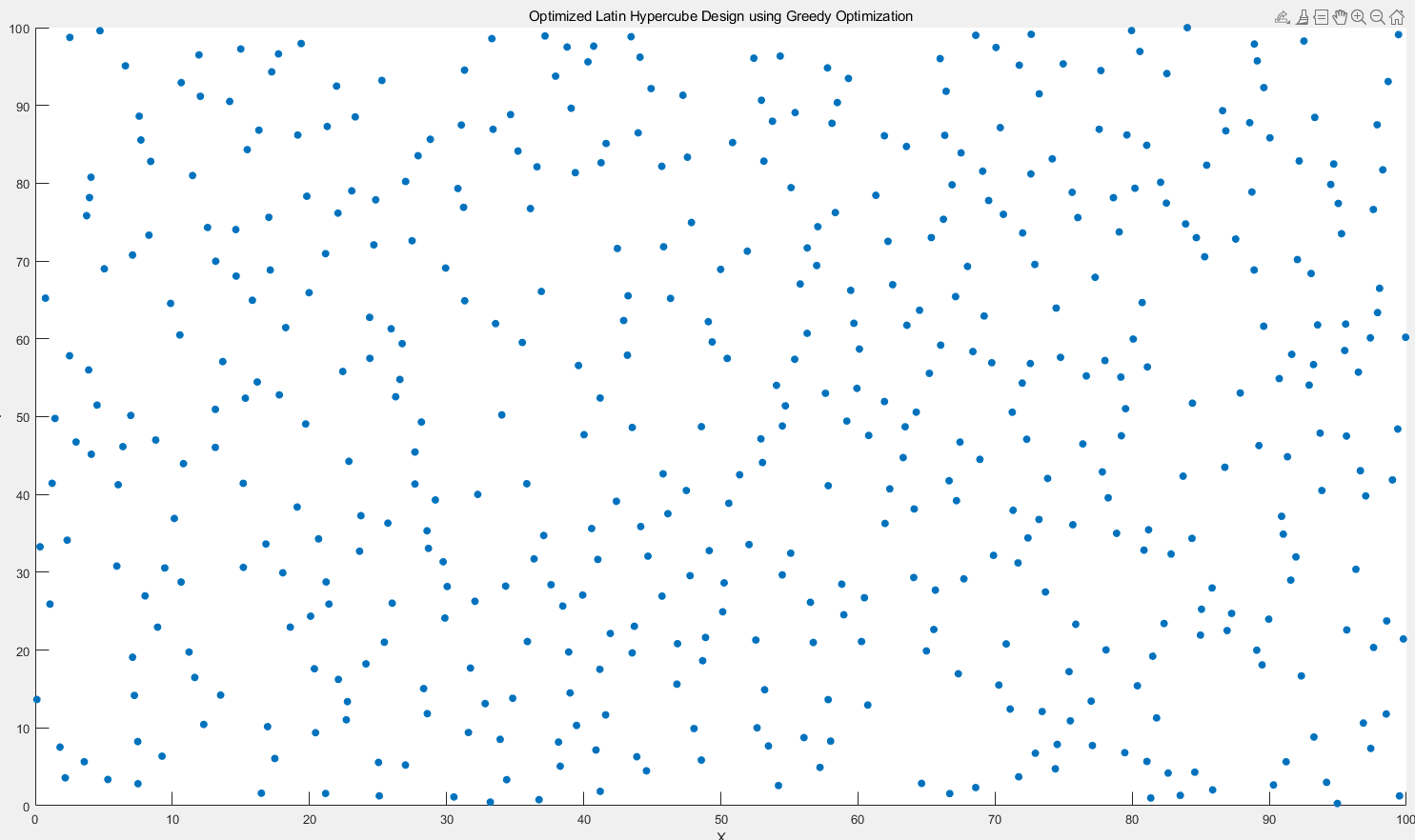
迭代1000次

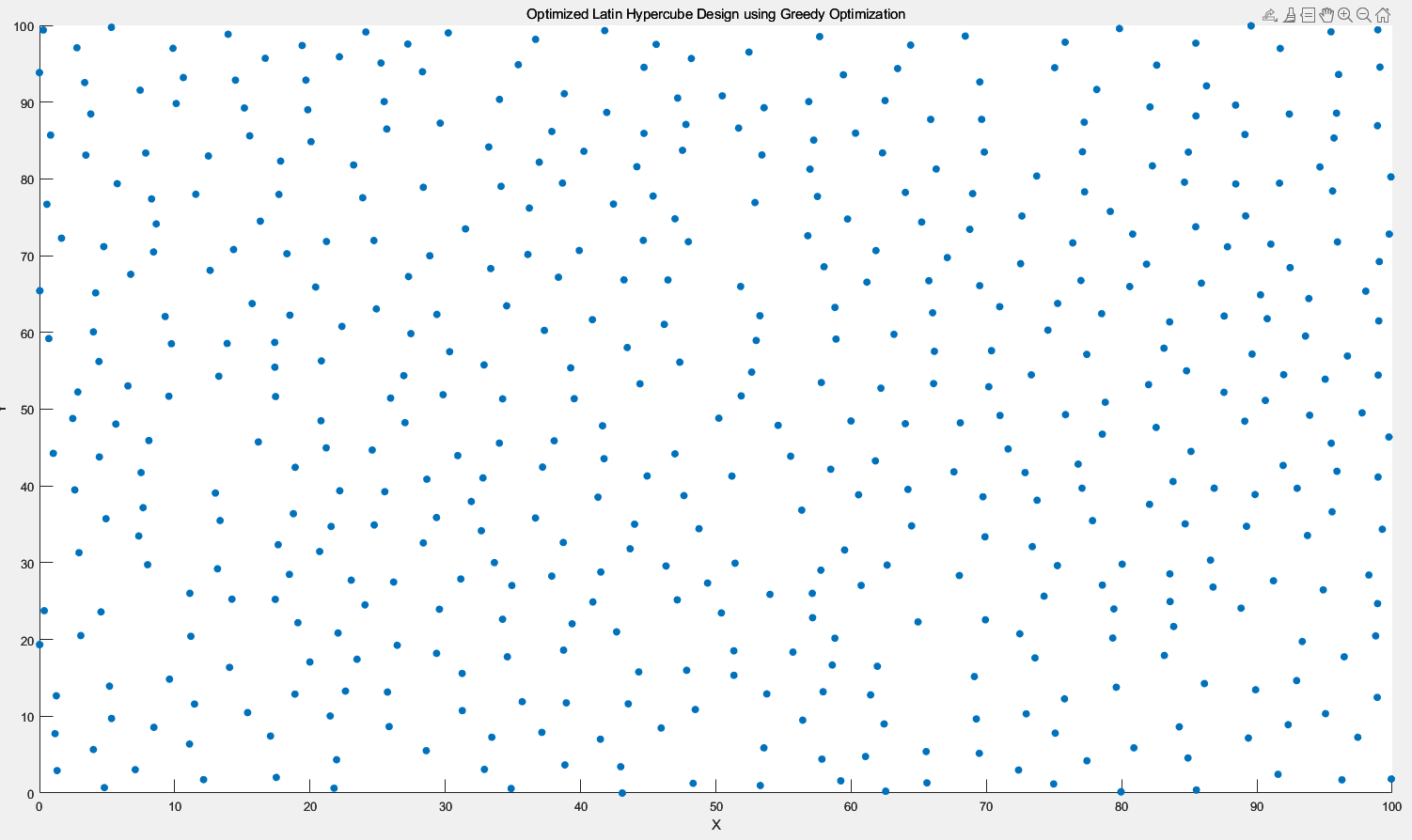
迭代10000次

迭代100000次

3.4.3 三维情况下

三维就看不出来了