觉得这篇文章写得蛮清楚的,mark
转载自https://blog.csdn.net/gogoaway/article/details/53445670
1 AUC,ROC简单解释
ROC(Receiver Operating Characteristic)曲线的横坐标为TNR(负样本正确率),纵坐标为TPR(正样本正确率),以下为关于TPR,TNR的一些摘抄:
True Positive (真正, TP)被模型预测为正的正样本;可以称作判断为真的正确率
True Negative(真负 , TN)被模型预测为负的负样本 ;可以称作判断为假的正确率
False Positive (假正, FP)被模型预测为正的负样本;可以称作误报率
False Negative(假负 , FN)被模型预测为负的正样本;可以称作漏报率
True Positive Rate(真正率 , TPR)或灵敏度(sensitivity) TPR = TP /(TP + FN)
正样本预测结果数 / 正样本实际数True Negative Rate(真负率 , TNR)或特指度(specificity) TNR = TN /(TN + FP)
负样本预测结果数 / 负样本实际数False Positive Rate (假正率, FPR) FPR = FP /(FP + TN) 被预测为正的负样本结果数
/负样本实际数False Negative Rate(假负率 , FNR) FNR = FN /(TP + FN)
ROC曲线最直观的画法就是将所有样本按模型打分从高到低排序,然后将每一个样本定为阈值,算一个tpr,tnr出来做图,这样的python代码实现见如下:
http://kubicode.me/2016/09/19/Machine%20Learning/AUC-Calculation-by-Python/
但是如果用AUC算法的物理意义(即任意正样本排序前与负样本)来考虑,代码可以实现为如下一行(水平不够,只是摘抄而已):
R语言
auc <- mean(sample(pos.decision,1000,replace=T) > sample(neg.decision,1000,replace=T))
- 1
- 2
- 3
scala
val auc = list.sortBy(_._1).foldLeft((0, 0, 0))((a, b) => if (b._2 > 0) (a._1 + 1, a._2 + a._3, a._3) else (a._1, a._2, a._3 + 1)) match {case(a, b, c) => (1.0 * b / (a * c))}- 1
- 2
2 对于AUC物理意义的理解
可以通过举例来理解。
(部分示例来自http://blog.csdn.net/cherrylvlei/article/details/52958720)
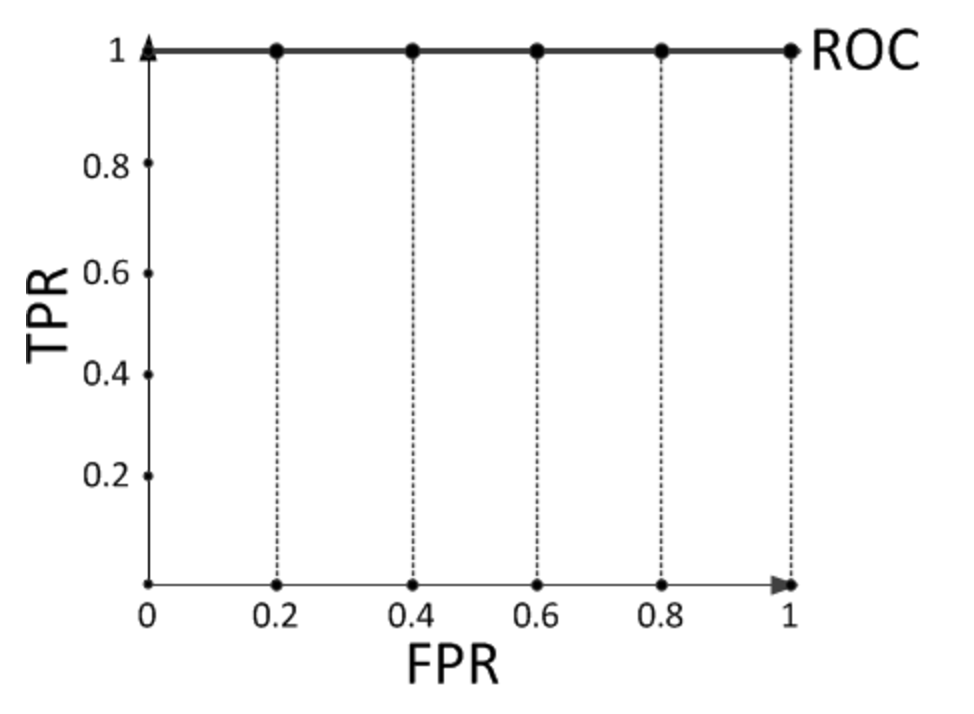
现在假设有一个训练好的二分类器对10个正负样本(正例5个,负例5个)预测,得分按高到低排序得到的最好预测结果为[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],即5个正例均排在5个负例前面,正例排在负例前面的概率为100%。然后绘制其ROC曲线,由于是10个样本,除开原点我们需要描10个点,如下:
描点方式按照样本预测结果的得分高低从左至右开始遍历。从原点开始,每遇到1便向y轴正方向移动y轴最小步长1个单位,这里是1/5=0.2;每遇到0则向x轴正方向移动x轴最小步长1个单位,这里也是0.2。不难看出,上图的AUC等于1,印证了正例排在负例前面的概率的确为100%。
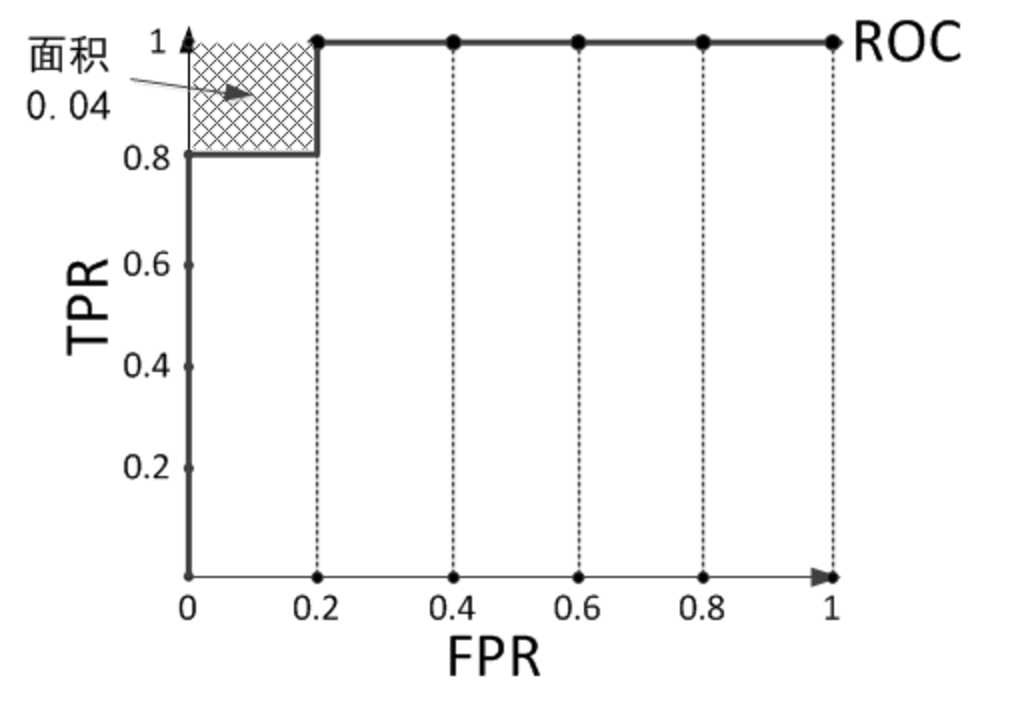
我们不妨再举个栗子,预测结果序列为[1, 1, 1, 1, 0, 1, 0, 0, 0, 0]。
计算上图的AUC为0.96与计算正例与排在负例前面的概率0.8 × 1 + 0.2 × 0.8 = 0.96相等,而左上角阴影部分的面积则是负例排在正例前面的概率0.2 × 0.2 = 0.04。
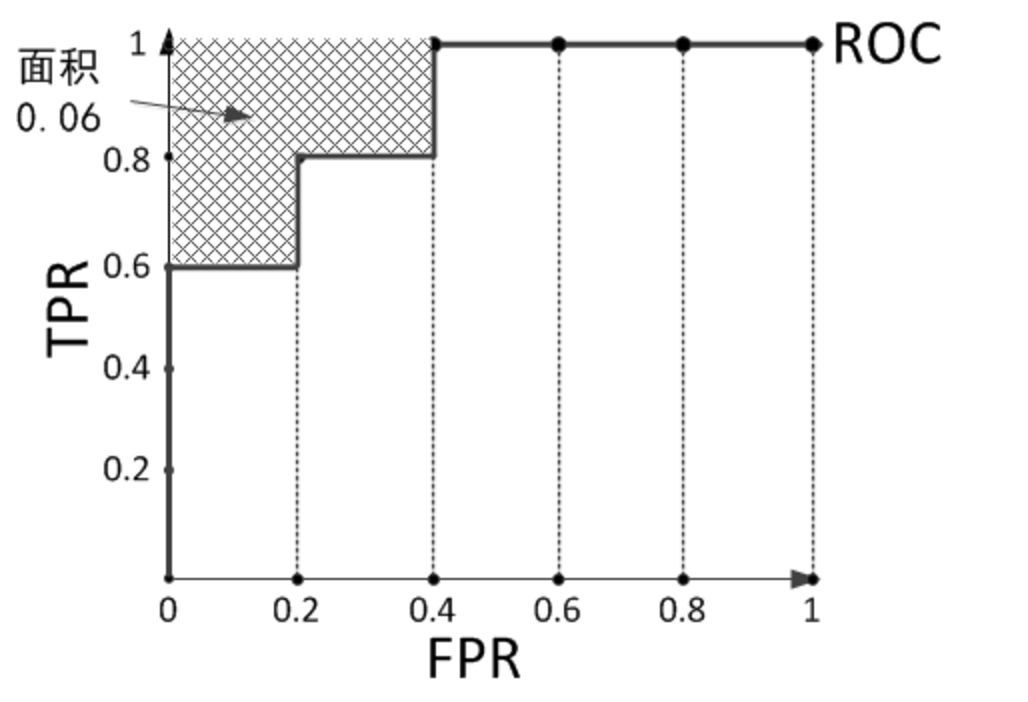
再看个栗子,预测结果序列为[1, 1, 1, 0, 1, 0, 1, 0, 0, 0]。
计算上图的AUC为0.88与计算正例与排在负例前面的概率0.6 × 1 + 0.2 × 0.8 + 0.2 × 0.6 = 0.88相等,左上角阴影部分的面积是负例排在正例前面的概率0.2 × 0.2 × 3 = 0.12。
根据上述排列为【1,1,1,0,1,0,1,0,0,0】的例子,尝试计算ROC曲线下面积和任意正例排序先于负例概率相同。假设所有正例数为P,所有负例数为N,对第i个正例,排在其后的负例数为Ni,排在其前的负例数为Ni’,则ROC下面积可以计算为:
area = 1/P*(N2’ - N1’)/N +2/P(N3’-N2’)/N + 3/P(N4’-N3’)/N+4/P(N5’-N4’)+5/P(N-N5’)/N
(即第一个、第二个。。。第五个小长方形之和)
化简后: area = (1/(P*N))*((N-N1’) +(N-N2’)+(N-N3’)+(N-N4’)+(N-N5’))
而任意正例排序先于负例概率可通过枚举法计算,第一个正例在任一负例之前的概率+第二个正例在任一负例之前的概率。。。+第五个正例在任一负例之前的概率。
probability = (1/P )*N1/N +(1/P )*N2/N +(1/P )*N3/N +(1/P )*N4/N +(1/P )*N5/N
化简后
probability =(1/P*N)(N1+N2+N3+N4+N5)
因为Ni = N - Ni’
所以 probabilty = area