最小二乘法的多项式拟合原理与代码实现

最小二乘法的多项式拟合
给定一系列点，运用最小二乘法拟合出这些点的多项式曲线函数。假设拟合出的多项式(k项)函数为：

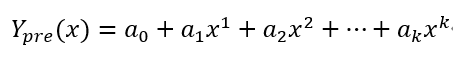
又假设真实曲线函数为:

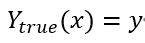
则对于给定的n个点(xi,yi ),0<i≤n，拟合曲线与实际偏差要最小，即：

则问题转换为：求一组解(a0,a1,a2,…,ak)^T，使得函数L的值最小。由极值条件可知，让L取最小值时的一组解，L对其的偏导数为0；为了求解，对L求ai的偏导并令其为0：

化简可得：

表示成矩阵为：

明显上式是一个解线性方程组问题：A*X=B。

在编程时，对于A的获取不必计算(k+1)^2次，可以发现A中的元素仅有2k+1种：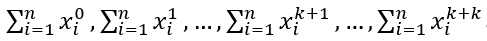
因此编程时仅需先算出这2k+1项，再将其按规律填入A即可。下面的示例代码演示了用Eigen库的Qr分解算法求解A*X=B问题。

#include <Eigen/Dense> 
//--Input
//---x:数据点的x坐标值数组
//---y:数据点的y坐标值数组
//---n:数据点的个数
//---k:多项式的阶
//--Output
//---返回A*X=B中的解X
Eigen::VectorXd polynomialFitting(double*x, double*y, unsigned n, unsigned k)
{
    
    
    Eigen::MatrixXd A=Eigen::MatrixXd::Zero(k+1,k+1);
    Eigen::VectorXd B=Eigen::VectorXd::Zero(k+1);

    double*x_pow_sum=new double[2*k+1];//存放A中2k+1项不重复元素
    for(unsigned i=0;i<2*k+1;i++)
    {
    
    
        double sum=0.;
        for(unsigned j=0;j<n;j++)
        {
    
    
            sum+=pow(x[j],i);//计算每项幂的和
        }
        x_pow_sum[i]=sum;//
    }
    for(unsigned i=0;i<k+1;i++)
    {
    
    
        for(unsigned j=0;j<k+1;j++)
        {
    
    
            A(i,j)=x_pow_sum[i+j];//按规律将2k+1项不重复元素填入矩阵A
        }
    }
    for(unsigned i=0;i<k+1;i++)
    {
    
    
        double sum=0;
        for(unsigned j=0;j<n;j++)
        {
    
    
            sum=sum+pow(x[j],i)*y[j];//计算B的每个元素
        }
        B[i]=sum;
    }
    //利用Eigen库中的Qr分解求解X
    Eigen::VectorXd X=A.colPivHouseholderQr().solve(B);
    return X;
}

若没有安装Eigen库，则可利用高斯消元法或者选列主元法的方式编写求解代码。