题目
下面一共有七道有关图的课后习题,全部都是思路画图题并不是算法设计题故在此就一起列举出来了~
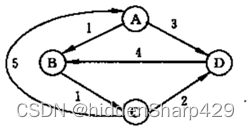
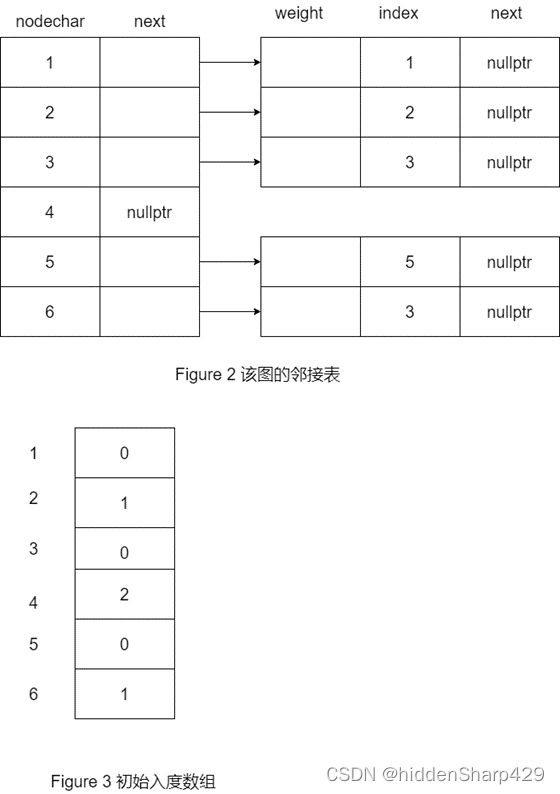
1. 已知如下图所示的有向图,请回答下面几个问题
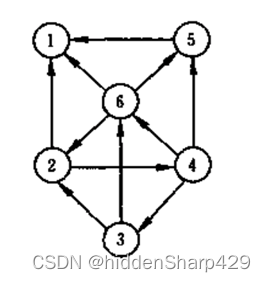
- 每个顶点的入/出度;
- 邻接矩阵;
- 邻接表;
- 逆邻接表;
- 强连通分量
解答
每个顶点的入/出度
(下面将用①+来表示①顶点的入度,①-代表出度,其他顶点类推)
| 顶点出度 | 顶点入度 |
|---|---|
| ①+:3 | ①-:0 |
| ②+:2 | ②-:2 |
| ③+:1 | ③-:2 |
| ④+:1 | ④-:3 |
| ⑤+:2 | ⑤-:1 |
| ⑥+:2 | ⑥-:3 |
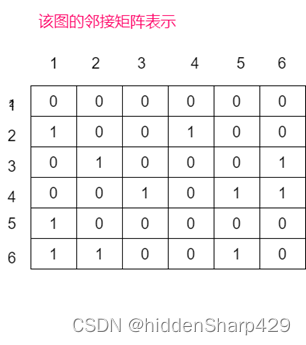
邻接矩阵
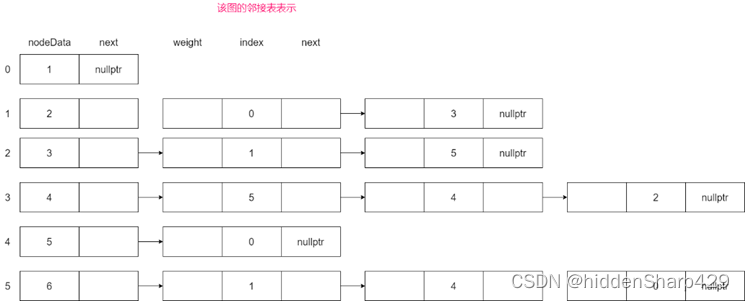
邻接表
逆邻接表
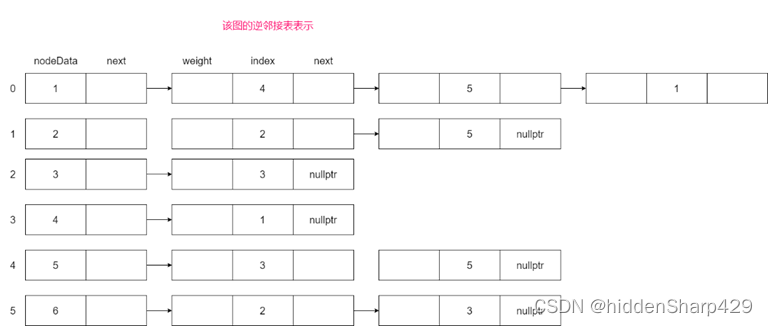
强连通分量
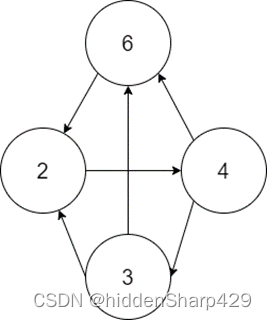
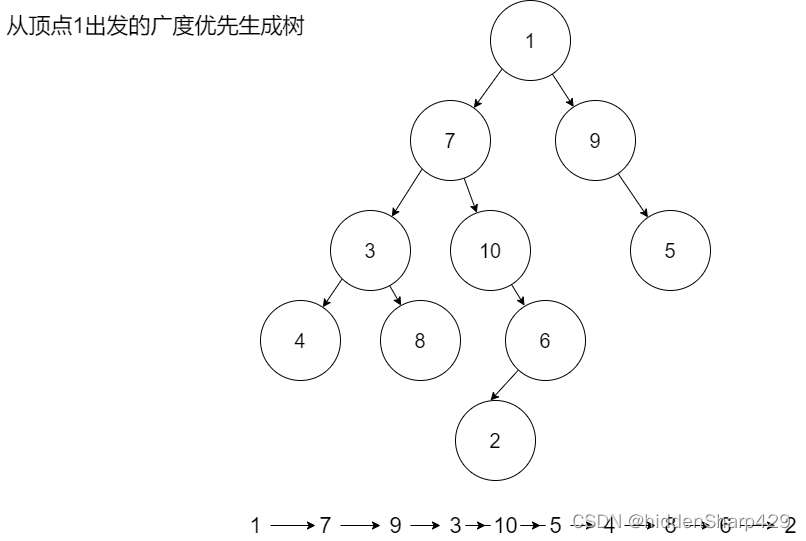
2. 已知二维数组表示的图的邻接矩阵如下图所示,分别画出自顶点1出发进行遍历所得的深度优先生成树和广度优先生成树。
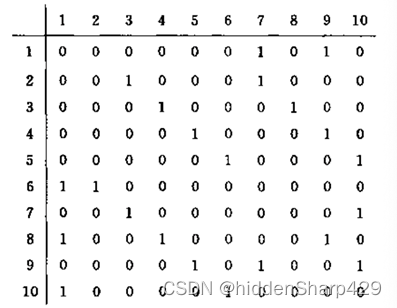
解答
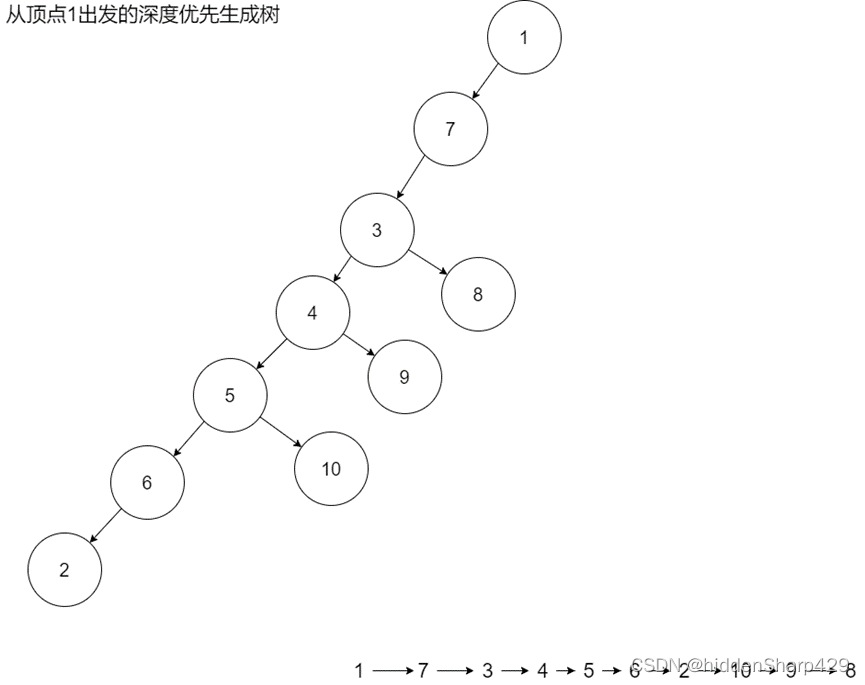
顶点1出发进行遍历所得的深度优先生成树
顶点1出发进行遍历所得的广度优先生成树
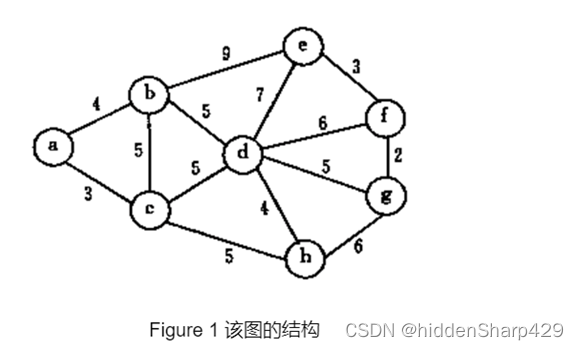
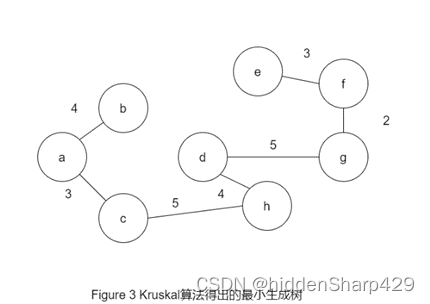
3.针对下图回答下面两个问题
扫描二维码关注公众号,回复:
15748358 查看本文章


- 写出其邻接矩阵,并按Prim算法求其最小生成树
- 写出其邻接表,并按Kruskal算法求其最小生成树
解答
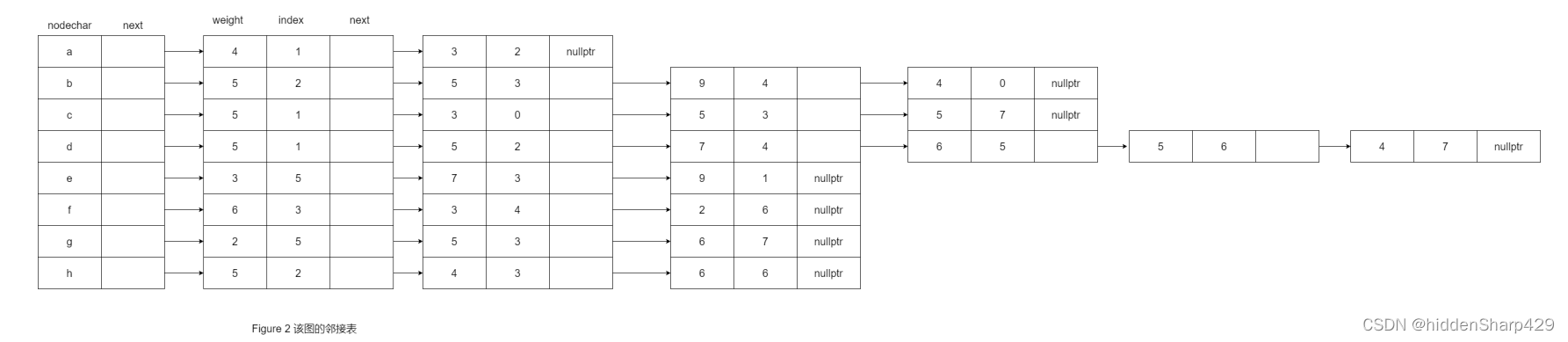
写出其邻接矩阵,并按Prim算法求其最小生成树


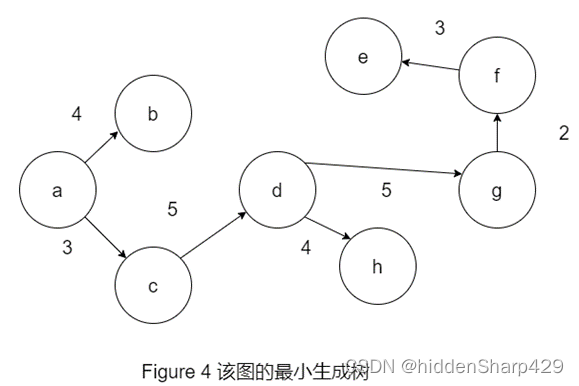
写出其邻接表,并按Kruskal算法求其最小生成树
4. 针对下图回答下面两个问题
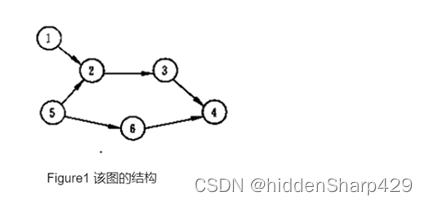
- 列出全部可能的拓扑有序序列
- 写出其邻接表, 并指出应用课上所学的TopLogicalSort算法求得的是哪一个序列
解答
列出全部可能的拓扑有序序列
- 152634
- 512634
- 156234
- 516234
写出其邻接表, 并指出应用课上所学的TopLogicalSort算法求得的是哪一个序列
使用课上所学的TopLogicalSort算法得出的序列是:563412
5. 针对下图AOE网络,计算个活动弧和顶点的相关值
计算个弧的 e ( a i ) , l ( a i ) 的值、各事件(顶点)的 v e ( v i ) , l ( v i ) 计算个弧的e(a_i),l(a_i)的值、各事件(顶点)的ve(v_i),l(v_i) 计算个弧的e(ai),l(ai)的值、各事件(顶点)的ve(vi),l(vi)
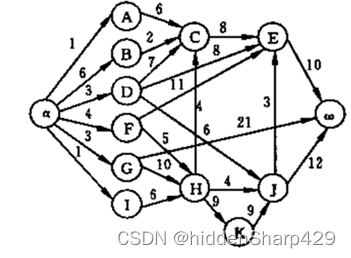
解答
各个弧和顶点的编号如下图所示
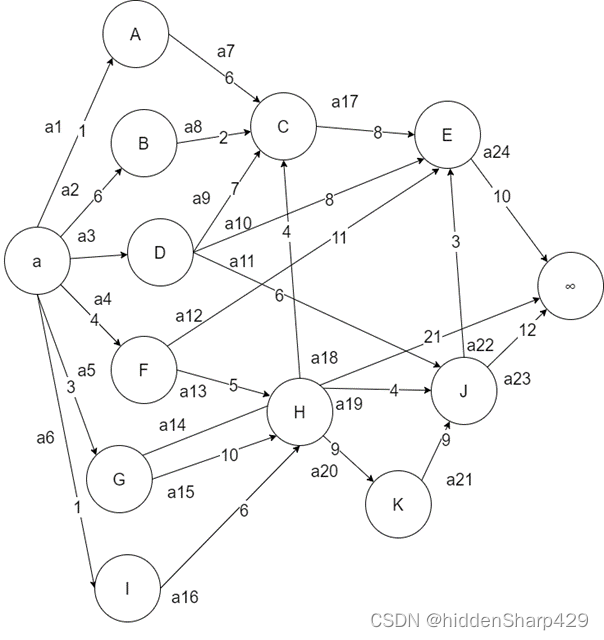
V e ( v i ) Ve(v_i) Ve(vi)
- V e ( A ) = 1 Ve(A) = 1 Ve(A)=1
- V e ( B ) = 6 Ve(B) = 6 Ve(B)=6
- V e ( C ) = 17 ( a → G → H → C ) Ve(C) = 17(a→G→H→C) Ve(C)=17(a→G→H→C)
- V e ( D ) = 3 Ve(D) = 3 Ve(D)=3
- V e ( E ) = 25 ( a → G → H → C → E ) Ve(E) = 25(a→G→H→C→E) Ve(E)=25(a→G→H→C→E)
- V e ( F ) = 4 Ve(F) = 4 Ve(F)=4
- V e ( G ) = 3 Ve(G) = 3 Ve(G)=3
- V e ( H ) = 13 ( a → G → H ) Ve(H) = 13(a→G→H) Ve(H)=13(a→G→H)
- V e ( I ) = 1 Ve(I) = 1 Ve(I)=1
- V e ( J ) = 31 ( a → G → H → K → J ) Ve(J) = 31(a→G→H→K→J) Ve(J)=31(a→G→H→K→J)
- V e ( K ) = 22 ( a → G → H → K ) Ve(K) = 22(a→G→H→K) Ve(K)=22(a→G→H→K)
- V e ( ∞ ) = 43 Ve(∞) = 43 Ve(∞)=43
I ( v i ) I(v_i) I(vi)
- I ( A ) = 19 I(A) = 19 I(A)=19
- I ( B ) = 23 I(B) = 23 I(B)=23
- I ( C ) = 25 I(C) = 25 I(C)=25
- I ( D ) = 18 I(D) = 18 I(D)=18
- I ( E ) = 33 I(E) = 33 I(E)=33
- I ( F ) = 8 I(F) = 8 I(F)=8
- I ( G ) = 3 I(G) = 3 I(G)=3
- I ( H ) = 13 I(H) = 13 I(H)=13
- I ( I ) = 7 I(I) = 7 I(I)=7
- I ( J ) = 31 I(J) = 31 I(J)=31
- I ( K ) = 22 I(K) = 22 I(K)=22
- I ( ∞ ) = 43 I(∞) = 43 I(∞)=43
e ( a i ) e(a_i) e(ai)
- e ( a 1 ) = 0 e(a_1) = 0 e(a1)=0
- e ( a 2 ) = 0 e(a_2) = 0 e(a2)=0
- e ( a 3 ) = 0 e(a_3) = 0 e(a3)=0
- e ( a 4 ) = 0 e(a_4) = 0 e(a4)=0
- e ( a 5 ) = 0 e(a_5) = 0 e(a5)=0
- e ( a 6 ) = 0 e(a_6) = 0 e(a6)=0
- e ( a 8 ) = 6 e(a_8) = 6 e(a8)=6
- e ( a 9 ) = 3 e(a_9) = 3 e(a9)=3
- e ( a 10 ) = 3 e(a_{10}) = 3 e(a10)=3
- e ( a 11 ) = 3 e(a_{11}) = 3 e(a11)=3
- e ( a 12 ) = 4 e(a_{12}) = 4 e(a12)=4
- e ( a 13 ) = 4 e(a_{13}) = 4 e(a13)=4
- e ( a 14 ) = 3 e(a_{14}) = 3 e(a14)=3
- e ( a 15 ) = 3 e(a_{15}) = 3 e(a15)=3
- e ( a 16 ) = 1 e(a_{16}) = 1 e(a16)=1
- e ( a 17 ) = 17 e(a_{17}) = 17 e(a17)=17
- e ( a 18 ) = 13 e(a_{18}) = 13 e(a18)=13
- e ( a 19 ) = 13 e(a_{19}) = 13 e(a19)=13
- e ( a 20 ) = 13 e(a_{20}) = 13 e(a20)=13
- e ( a 21 ) = 22 e(a_{21}) = 22 e(a21)=22
- e ( a 22 ) = 31 e(a_{22}) = 31 e(a22)=31
- e ( a 23 ) = 31 e(a_{23}) = 31 e(a23)=31
- e ( a 24 ) = 25 e(a_{24}) = 25 e(a24)=25
l ( a i ) l(a_i) l(ai)
- l ( a 1 ) = 18 l(a_1) = 18 l(a1)=18
- l ( a 2 ) = 17 l(a_2) = 17 l(a2)=17
- l ( a 3 ) = 15 l(a_3) = 15 l(a3)=15
- l ( a 4 ) = 4 l(a_4) = 4 l(a4)=4
- l ( a 5 ) = 0 l(a_5) = 0 l(a5)=0
- l ( a 6 ) = 6 l(a_6) = 6 l(a6)=6
- l ( a 7 ) = 19 l(a_7) = 19 l(a7)=19
- l ( a 8 ) = 22 l(a_8) = 22 l(a8)=22
- l ( a 9 ) = 18 l(a_9) = 18 l(a9)=18
- l ( a 10 ) = 25 l(a_{10}) = 25 l(a10)=25
- l ( a 11 ) = 25 l(a_{11}) = 25 l(a11)=25
- l ( a 12 ) = 27 l(a_{12}) = 27 l(a12)=27
- l ( a 13 ) = 8 l(a_{13}) = 8 l(a13)=8
- l ( a 14 ) = 22 l(a_{14}) = 22 l(a14)=22
- l ( a 15 ) = 3 l(a_{15}) = 3 l(a15)=3
- l ( a 16 ) = 7 l(a_{16}) = 7 l(a16)=7
- l ( a 17 ) = 25 l(a_{17}) = 25 l(a17)=25
- l ( a 18 ) = 21 l(a_{18}) = 21 l(a18)=21
- l ( a 19 ) = 27 l(a_{19}) = 27 l(a19)=27
- l ( a 20 ) = 13 l(a_{20}) = 13 l(a20)=13
- l ( a 21 ) = 22 l(a_{21}) = 22 l(a21)=22
- l ( a 22 ) = 30 l(a_{22}) =30 l(a22)=30
- l ( a 23 ) = 31 l(a_{23}) = 31 l(a23)=31
- l ( a 24 ) = 33 l(a_{24}) = 33 l(a24)=33
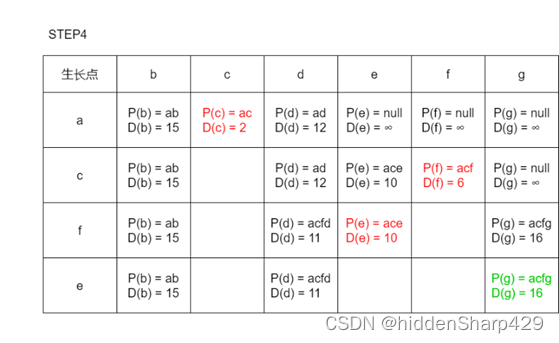
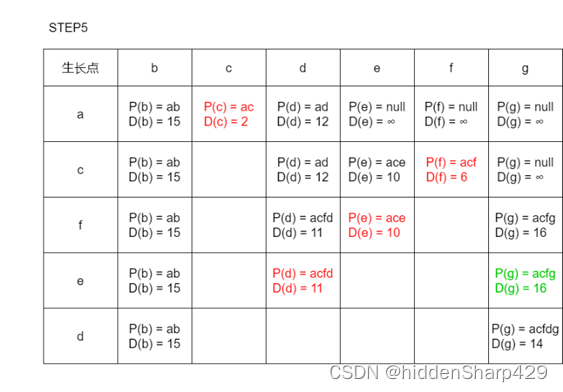
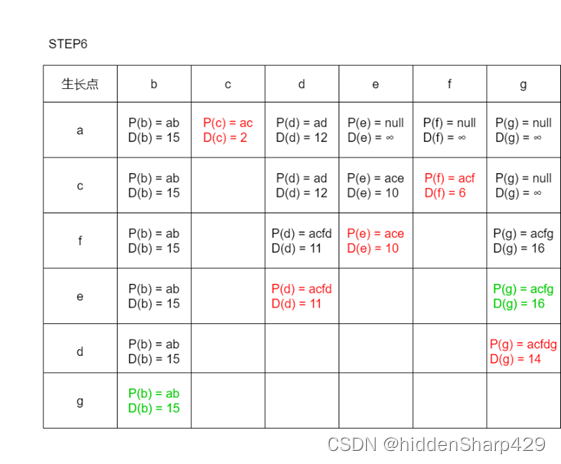
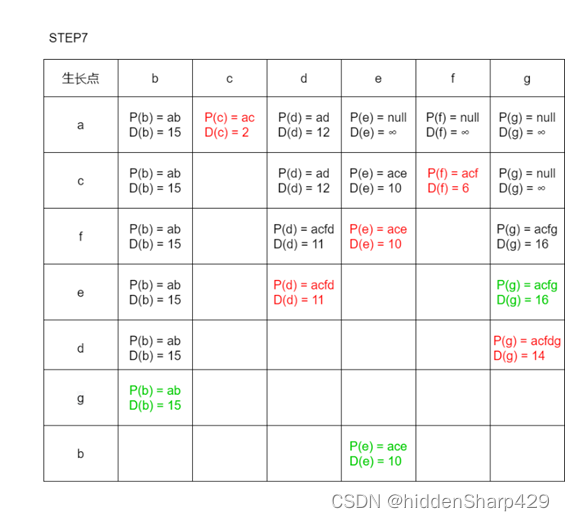
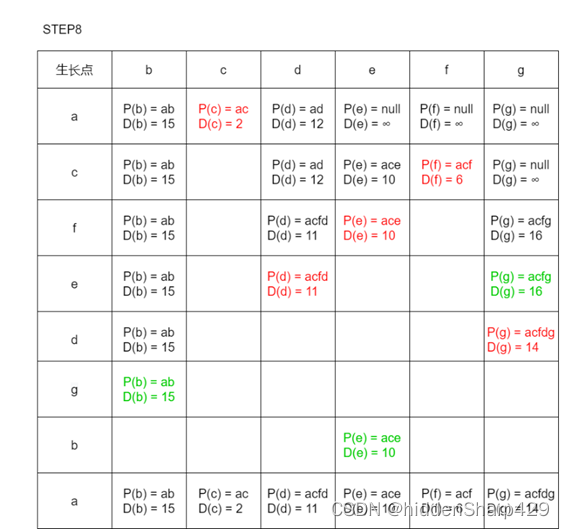
6. 利用Dijkstra算法,求图中顶点a到其他各顶点的最短路径,写出执行算法过程中各步的状态
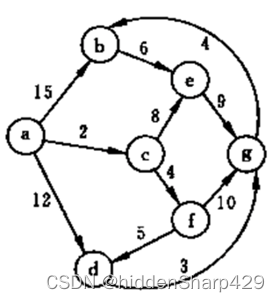
解答
步骤一
以a为起点初始待定路径表

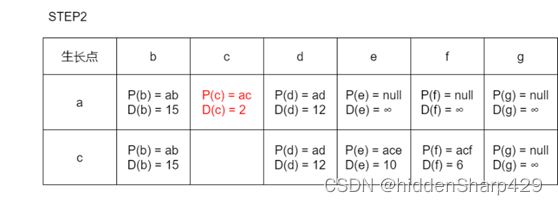
步骤二
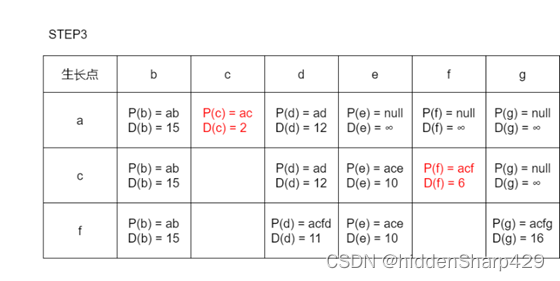
从待定路径表中选出一条最短的边,设其顶点为新的生长点,并且对剩下每一个生长点进行比较,若以新生长点为中转的路径短于原始路径则替换。
往后的步骤
对步骤二进行n-2次重复(注:绿色表示当前有新的通路,但路径长度大于原来的路径故步替换,红色为新的通路的路径长度小于原来路径的长度故替换)
7. 利用Floyd算法,求图中各对顶点间的最短路径
解答
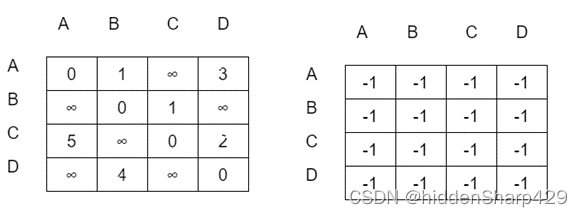
STEP1:初始邻接矩阵D,和Path
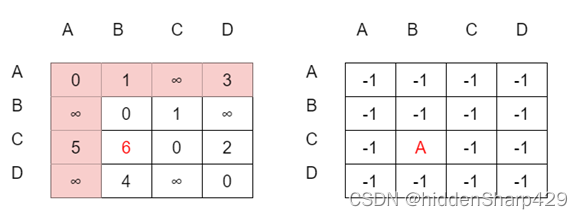
STEP2:以A为中转点,进行第一次迭代
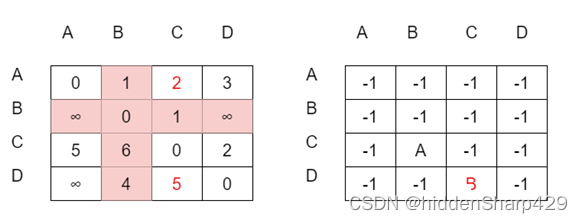
STEP3:以B为中转点,进行第二次迭代
STEP4:以C为中转点,进行第三次迭代
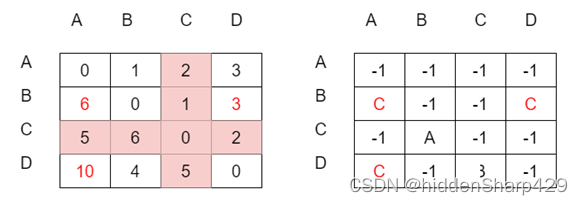
STEP5:以D为中转点,进行第四次迭代
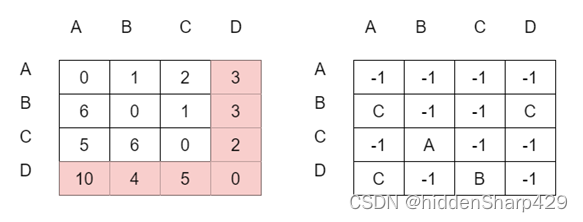
STEP6:得出最终的D,和Path矩阵
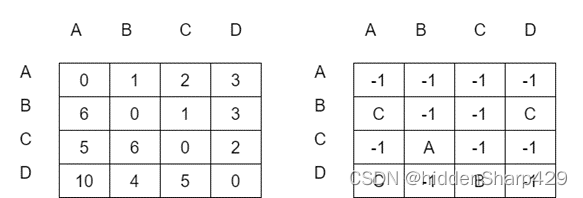
结束语
因为是算法小菜,所以提供的方法和思路可能不是很好,请多多包涵~如果有疑问欢迎大家留言讨论,你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗?我们之间的交流是我最大的动力!