实验四 图的遍历
一、实验目的
掌握图的概念和结构特征,以及各种存储结构的特点及适用范围; 掌握图的建立、图的深度优先搜索和广度优先搜索。
二、实验环境
1、PC微机;
2、Windows 操作系统;
3、VC6.0或以上
三、实验内容
利用邻接矩阵作存储结构,编写图的深度优先搜索和广度优先搜索。
测试数据:
6 9 //顶点数 边数
ABCDEF //顶点
0,1 0,2 0,4 1,2 1,3 2,3 2,5 3,4 3,5
输出该图深度优先搜索和广度优先搜索访问顺序。
四、实验步骤、测试及结果
1.代码
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXVEX 100 /* 最大顶点数,应由用户定义 */
#define INFINITY 65535 /* 无穷大 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
typedef struct
{
VertexType vexs[MAXVEX]; /* 顶点表 */
EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */
int numNodes, numEdges; /* 图中当前的顶点数和边数 */
}MGraph;
/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph *G)
{
int i,j,k,w;
printf("输入顶点数和边数(英文输入):\n");
scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */
for(i = 0;i <G->numNodes;i++) /* 读入顶点信息,建立顶点表 */
scanf(&G->vexs[i]);
for(i = 0;i <G->numNodes;i++)
for(j = 0;j <G->numNodes;j++)
G->arc[i][j]=INFINITY; /* 邻接矩阵初始化 */
for(k = 0;k <G->numEdges;k++) /* 读入numEdges条边,建立邻接矩阵 */
{
printf("输入边(vi,vj)上的下标i,下标j和权w:\n");
scanf("%d,%d,%d",&i,&j,&w); /* 输入边(vi,vj)上的权w */
G->arc[i][j]=w;
G->arc[j][i]= G->arc[i][j]; /* 因为是无向图,矩阵对称 */
}
}
int main(void)
{
MGraph G;
CreateMGraph(&G);
for(int i=0; i<G.numNodes; i++)
{
for(int j=0; j<G.numNodes;j++)
{
printf("%8d", G.arc[i][j]);
}
printf("\n");
}
return 0;
}
运行结果

二、
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */
typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
#define MAXSIZE 6 /* 存储空间初始分配量 */
#define MAXEDGE 9
#define MAXVEX 9
#define INFINITY 65535
typedef struct
{
VertexType vexs[MAXVEX]; /* 顶点表 */
EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */
int numVertexes, numEdges; /* 图中当前的顶点数和边数 */
}MGraph;
/* 用到的队列结构与函数********************************** */
/* 循环队列的顺序存储结构 */
typedef struct
{
int data[MAXSIZE];
int front; /* 头指针 */
int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */
}Queue;
/* 初始化一个空队列Q */
Status InitQueue(Queue *Q)
{
Q->front=0;
Q->rear=0;
return OK;
}
/* 若队列Q为空队列,则返回TRUE,否则返回FALSE */
Status QueueEmpty(Queue Q)
{
if(Q.front==Q.rear) /* 队列空的标志 */
return TRUE;
else
return FALSE;
}
/* 若队列未满,则插入元素e为Q新的队尾元素 */
Status EnQueue(Queue *Q,int e)
{
if ((Q->rear+1)%MAXSIZE == Q->front) /* 队列满的判断 */
return ERROR;
Q->data[Q->rear]=e; /* 将元素e赋值给队尾 */
Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置, */
/* 若到最后则转到数组头部 */
return OK;
}
/* 若队列不空,则删除Q中队头元素,用e返回其值 */
Status DeQueue(Queue *Q,int *e)
{
if (Q->front == Q->rear) /* 队列空的判断 */
return ERROR;
*e=Q->data[Q->front]; /* 将队头元素赋值给e */
Q->front=(Q->front+1)%MAXSIZE; /* front指针向后移一位置, */
/* 若到最后则转到数组头部 */
return OK;
}
void CreateMGraph(MGraph *G)
{
int i, j;
G->numEdges=9;
G->numVertexes=6;
/* 读入顶点信息,建立顶点表 */
G->vexs[0]='A';
G->vexs[1]='B';
G->vexs[2]='C';
G->vexs[3]='D';
G->vexs[4]='E';
G->vexs[5]='F';
for (i = 0; i < G->numVertexes; i++)/* 初始化图 */
{
for ( j = 0; j < G->numVertexes; j++)
{
G->arc[i][j]=0;
}
}
G->arc[0][1]=1;
G->arc[0][2]=1;
G->arc[0][4]=1;
G->arc[1][2]=1;
G->arc[1][3]=1;
G->arc[2][3]=1;
G->arc[2][5]=1;
G->arc[3][4]=1;
G->arc[3][5]=1;
for(i = 0; i < G->numVertexes; i++)
{
for(j = i; j < G->numVertexes; j++)
{
G->arc[j][i] =G->arc[i][j];
}
}
}
Boolean visited[MAXVEX]; /* 访问标志的数组 */
/* 邻接矩阵的深度优先递归算法 */
void DFS(MGraph G, int i)
{
int j;
visited[i] = TRUE;
printf("%c ", G.vexs[i]);/* 打印顶点,也可以其它操作 */
for(j = 0; j < G.numVertexes; j++)
if(G.arc[i][j] == 1 && !visited[j])
DFS(G, j);/* 对为访问的邻接顶点递归调用 */
}
/* 邻接矩阵的深度遍历操作 */
void DFSTraverse(MGraph G)
{
int i;
for(i = 0; i < G.numVertexes; i++)
visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */
for(i = 0; i < G.numVertexes; i++)
if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */
DFS(G, i);
}
/* 邻接矩阵的广度遍历算法 */
void BFSTraverse(MGraph G)
{
int i, j;
Queue Q;
for(i = 0; i < G.numVertexes; i++)
visited[i] = FALSE;
InitQueue(&Q); /* 初始化一辅助用的队列 */
for(i = 0; i < G.numVertexes; i++) /* 对每一个顶点做循环 */
{
if (!visited[i]) /* 若是未访问过就处理 */
{
visited[i]=TRUE; /* 设置当前顶点访问过 */
printf("%c ", G.vexs[i]);/* 打印顶点,也可以其它操作 */
EnQueue(&Q,i); /* 将此顶点入队列 */
while(!QueueEmpty(Q)) /* 若当前队列不为空 */
{
DeQueue(&Q,&i); /* 将队对元素出队列,赋值给i */
for(j=0;j<G.numVertexes;j++)
{
/* 判断其它顶点若与当前顶点存在边且未访问过 */
if(G.arc[i][j] == 1 && !visited[j])
{
visited[j]=TRUE; /* 将找到的此顶点标记为已访问 */
printf("%c ", G.vexs[j]); /* 打印顶点 */
EnQueue(&Q,j); /* 将找到的此顶点入队列 */
}
}
}
}
}
}
int main(void)
{
MGraph G;
CreateMGraph(&G);
printf("\n深度遍历:");
DFSTraverse(G);
printf("\n广度遍历:");
BFSTraverse(G);
return 0;
}
运行结果:
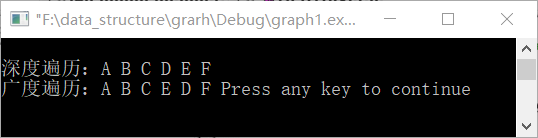
五、实验小结
- 深度优先遍历其实就是一个递归的过程,而且就像一棵树的前序遍历。它从图中某个顶点 v 出发,访问此顶点,然后从 v 的未被访问的邻接点出发深度优先遍历图,直至图中所有和 v 有路径相通的顶点都被访问到。
- 广度优先遍历就类似于树的层序遍历。