冈萨雷斯DIP第8章知识点

8.1 基础

图像中的冗余

1. 编码冗余：用于表示灰度的8比特编码所包含的比特数，要比表示该灰度所需要的比特数多。可通过变长编码来解决。

2. 空间和时间冗余：与相邻像素相似(图像)；时间：相邻帧中的像素(视频)。可以使用行程长度或者相邻像素的差。

3. 无关信息：被人类视觉系统忽略或与用途无关的信息，从未被利用的角度看，它是冗余的。消除冗余信息，量化。

度量图像信息

我们可以通过观察图像的直方图来估计该信源的符号概率。灰度信源的熵变为(可以达到的压缩的下界)

$$\tilde{H}=-\sum _{k=0}^{L-1}{p}_r\left(r_k\right){\log }_2{p}_r\left(r_k\right)$$

保真度准则

均方根误差(root-mean-square error) $e_{rms}$是整 $M\times N$ 阵列的平均均方误差的平方根，即：

$$e_{\mathrm{rms}}={\left[\frac{1}{MN}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}[\hat{f}(x,y)-f(x,y){]}^2\right]}^{1/2}$$

均方信噪比(mean square Signal-to-Noise Ratio, SNR) ${\mathrm{SNR}}_{ms}$

$${\mathrm{SNR}}_{\mathrm{ms}}=\frac{{\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}[\hat{f}(x,y){]}^2}{{\sum }_{x=0}^{M-1}{\sum }_{y=0}^{N-1}[\hat{f}(x,y)-f(x,y){]}^2}$$

8比特灰度图像，峰值信噪比(Peak Signal-to-Noise Ratio, $\mathrm{PSNR}$)定义为：

$$\mathrm{PSNR}=10{\log }_{10}\frac{255^2}{\mathrm{MSE}}(\mathrm{dB})$$

一般情况下，若输出图像的 PSNR>35dB，则肉眼无差别。

尽管客观保真度准则能够简单且方便地评价信息损失，但解压缩图像最终还得由人来观察；因此，根据人的主观评价来度量图像的质量通常更为合适。

通用图像压缩功能框图

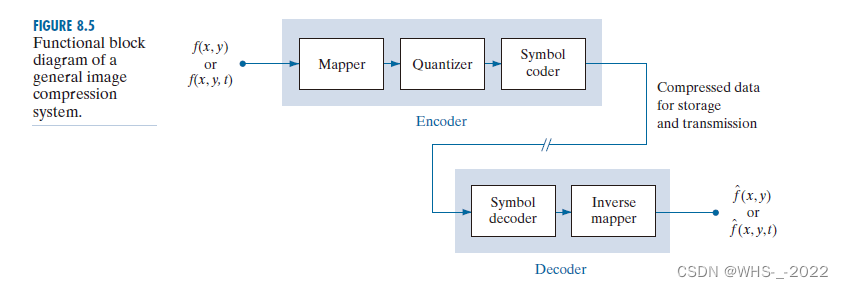
图像格式、压缩标准

算术编码 AC 最早在二值图像压缩标准 JBIG1、JBIG2（Joint Bi-level Image Experts Group）中使用，他受到美国专利保护。后来在最新的JPEG-2000、H.264、 MPEG4、AVC中使用。

H.264是视频会议、流媒体的编码标准，和 MPEG4、AVC是完全相同的。

JPEG中使用了块变换编码、霍夫曼编码、行程编码、DCT变换。

JPEG-2000中使用了算术编码和DWT编码，极大的提高了压缩性能。

HEVC（High Efficiency Video Coding）是最新的编码方案，又称H.265，用于4K视频应用。

MPEG-1 类似于H.261，但是它第一次提出了B帧，可以根据前后帧进行编码。

---

8.9 块变换编码

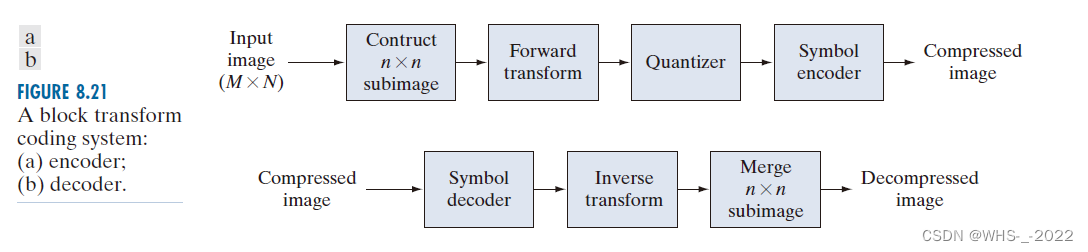
编码器执行 4 种相对简单的操作：子图像分解、变换、量化和编码 。

8.9.1 变换的选择

DCT的信息打包能力要强于DFT和WHT（Walsh-Hadamard变换）。

在信息打包方面的最佳变换是Karhunen-Loéve变换(KLT)。由于KLT是数据相关的，所以计算每幅子图像的KLT基图像并不容易。由于这个原因，实际上很少使用KLT来压缩图像。

DCT变换的优点：能用单片集成电路实现 可将最多信息打包到最少的系数中 对大多数图像而言 并且在子图像间的边界变得明显时 使出现的 块状外观 块伪影 块效应 blocking artifacts) 最小。

8.9.2 子图像尺寸选择

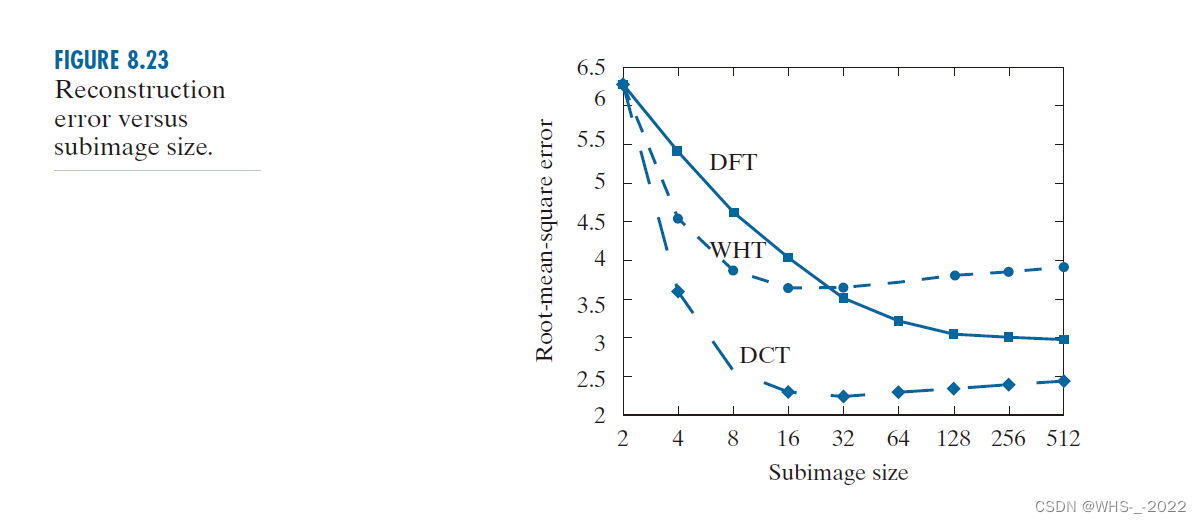
$16\times 16$ 是最佳的，但是因为历史原因，当时硬件显示，以前选择是 $8\times 8$。

8.9.3 比特分配

截断、量化和编码变换后子图像的系数的整个过程 通常称为比特分配 。

---

8.12 数字图像水印

鲁棒水印用于版权保护；脆弱水印用于篡改检测；半脆弱水印用于区分普通的图像处理和恶意篡改。

不可见性是通过将水印作为视觉上的冗余信息插入到图像中来保证的 。

相关系数度量水印的相似性

$$\gamma =\frac{{\sum }_{i=1}^K\left({\hat{\omega }}_i-\overline{\hat{\omega }}\right)\left({\omega }_i-\bar{\omega }\right)}{\sqrt{{\sum }_{i=1}^K{\left({\hat{\omega }}_i-\overline{\hat{\omega }}\right)}^2\cdot {\sum }_{i=1}^K{\left({\omega }_i-\bar{\omega }\right)}^2}}$$

水印容量、鲁棒性、不可见性质的矛盾

水印容量：水印容量指的是在一个数字媒体中可以嵌入的水印数据的量。较高的水印容量意味着可以嵌入更多的信息，从而提供更多的特定功能或实现更高的安全性，提高了水印的鲁棒性。然而，增加水印容量可能会对不可见性产生负面影响。

不可见性：不可见性是指数字水印在媒体中的视觉或感知影响。理想情况下，水印应该是不可察觉的，即嵌入的水印对媒体的质量或外观没有明显的影响。然而，提高不可见性可能会限制水印容量或降低鲁棒性。

鲁棒性：鲁棒性是指数字水印系统对一系列攻击或失真的抵抗能力。鲁棒性较高的水印能够在各种操作和攻击下仍然可靠地提取出来，而不会受到失真或恶意攻击的影响。然而，增加鲁棒性可能会需要增加水印容量同时降低不可见性。

---

8.7

$$\begin{array}{rl}\log q-H& =\log q\left[\sum _{j=1}^{q}P\left(a_j\right)\right]+\sum _{j=1}^{q}P\left(a_j\right)\log P\left(a_j\right)\\ & =\sum _{j=1}^{q}P\left(a_j\right)\log q+\sum _{j=1}^{q}P\left(a_j\right)\log P\left(a_j\right)\\ & =\sum _{j=1}^{q}P\left(a_j\right)\log qP\left(a_j\right)\end{array}$$

根据我们熟知的不等式 $1-1/x\le \ln x\le x-1$

$$\begin{array}{rl}\log q-H& \ge \sum _{j=1}^{q}P\left(a_j\right)\left[1-\frac{1}{qP\left(a_j\right)}\right]\\ & \ge \left[\sum _{j=1}^{q}P\left(a_j\right)-\frac{1}{q}\sum _{j=1}^q\frac{P\left(a_j\right)}{P\left(a_j\right)}\right]\\ & \ge 1-1\\ & \ge 0\end{array}$$

根据上述不等式的推导，只有当信号源是等概率的时候，信源的熵才能取最大值。