VINS-Mono之IMU预积分(Pre-integration)

1.前言

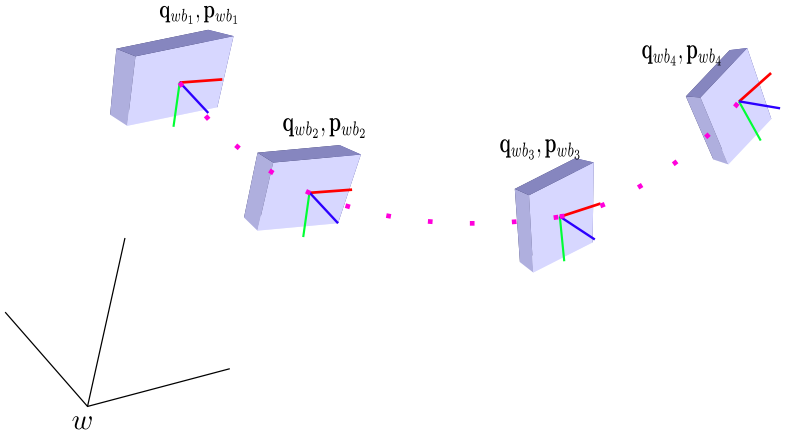
本博客基本上借鉴了崔华坤的《VINS论文推导及代码解析》和 VINS-Mono理论学习——IMU预积分 Pre-integration (Jacobian 协方差)的内容，因为确实写得太好了，然后有些地方加入自己一些理解。

VINS-MONO论文中的IV-B. IMU Pre-integration介绍了IMU预积分模型，Foster的倆篇论文对IMU预积分理论进行详细分析。

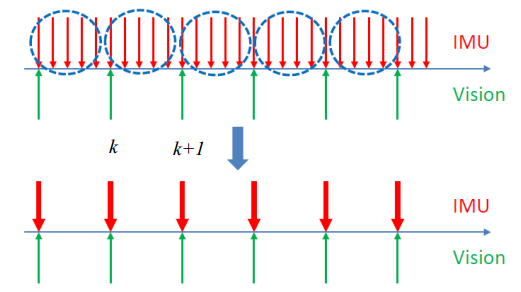
为什么需要对IMU进行预积分？
传统捷联惯性导航算法，在已知 $k$ 时刻下的IMU状态量(姿态、速度和位移)情况下，利用IMU测量的线加速度和角速度，通过积分预算得到 $k+1$时刻下的状态量。

然而在非线性优化的VIO中，各个节点的状态量都是估计值，当算法对这些状态量优化时，每次调整都需要在它们之间重新积分，导致绝对位姿被优化时对状态量进行重复积分。IMU预积分的提出使得优化算法可对IMU的相对测量进行处理，使它与绝对位姿解耦，或者只要线性运算就可以进行矫正。

2. IMU模型

IMU测量值包括加速度计得到的 (测量值) 线加速度 $\hat{a_{t}}$ 和陀螺仪得到的角加速度 $\hat{w}_{t}$ 【论文式(1)】
$\hat{a}_{t}=a_{t}+b_{at}+R_{w}^{t}g^{w}+n_{a}$ $\hat{w}_{t}=w_{t}+b_{wt}+n_{w}$其中 $t$下标表示在IMU的体(body)坐标系下， $a_{t}$、 $w_{t}$分别表示IMU真实的线加速度和角速度，并受到加速度偏置(bias) $b_{at}$、陀螺仪偏置 $b_{wt}$和附加噪声 $n_a$、 $n_{n_{w}}$的影响。计算得到的线加速度 $\hat{a_{t}}$是重力加速度和物体加速度的合矢量。
假设附加噪声为高斯噪声：
$n_{a}\sim(0,\sigma_{a}^{2}), \ n_{a}\sim(0,\sigma_{w}^{2})$ 加速度计偏置和陀螺仪偏置被建模为随机游走，其导数为高斯分布：【论文式(2)】
$\dot{b}_{at}=n_{ba}, \ \dot{b}_{wt}=n_{bw}$ $n_{ba}\sim N(0,\sigma_{ba}^{2}), \ n_{bw} \sim N(0, \sigma_{bw}^{2})$

3. 基于世界坐标系下的IMU运动模型

3.1 连续形式下的IMU运动模型

对于图像帧 $k$和 $k+1$, IMU body坐标系对应为 $b_{k}$和 $b_{k+1}$，位置、速度和姿态状态值PVQ(Pose、Velocity、Quaternion)可以根据 $[t_{k}, t_{k+1}]$时间间隔内的IMU测量值，在世界坐标系下进行传递：【论文式(3)(4)】
$p^{w}_{b_{k+1}}=p^{w}_{bk}+v_{b_{k}}^{w}\Delta t_{k}+\int \int_{t\in[t_{k}, t_{k+1}]}(R_{t}^{w}(\hat{a}_{t}-b_{at}-n_{a})-g^{w})dt^{2}$ $v_{b_{k+1}}^{w}=v_{bk}^{w}+\int_{t\in[t_{k},t_{k+1}]}(R^{w}_{t}(\hat{a}_{t}-b_{at}-n_{a})-g^{w})dt$ $q_{b_{k+1}}^{w} = q_{b_{k}}^{w} \otimes \int_{t\in[t_{k}, t_{k+1}]} \frac{1}{2} q_{t}^{b_{k}} \otimes \begin{bmatrix} (\hat{w}_{t}-b_{wt}-n_{w})\\ 0 \end{bmatrix}dt \\ = q_{bk} \otimes \int_{t\in[t_{k}, t_{k+1}]} \frac{1}{2} \Omega (\hat{w}_{t}-b_{wt}-n_{w})q_{t}^{bk}dt \tag{1}$ $\Omega(w)=\begin{bmatrix} -[w]_{\times} & w\\ -w^{T}& 0 \end{bmatrix}, \ [w]_{\times} = \begin{bmatrix} 0 & -w_{z} & w_{y}\\ w_{z} & 0 & -w_{x}\\ -w_{y} & w_{x} & 0 \end{bmatrix}$其中 $\Delta t_{k}$是 $[t_{k}, t_{k+1}]$之间的时间间隔， $R_{t}^{w}$为t时刻IMU body坐标系到世界坐标系的旋转矩阵， $q_{t}^{bk}$为用四元素表示的 $t$ 时刻从IMU body坐标系到 $k$ 时刻IMU body坐标系的旋转，这里的四元素实部在后，虚部在前。这里的 $\Omega(w)$表示四元素右乘。

---

关于公式 $(1)$的推导，这里首先引入四元素左乘右乘及导数定理：
根据《视觉SLAM14讲》3.4.2 的四元数乘法，我们引入左乘和右乘符号如下：
$q_{a} \otimes q_{b} = R(q_{b})q_{a} = \begin{bmatrix} s_{b} & z_{b} & -y_{b} & x_{b}\\ -z_{b} & s_{b} & x_{b} & y_{b}\\ y_{b}& -x_{b} & s_{b} & z_{b}\\ -x_{b}& -y_{b} & -z_{b} & s_{b} \end{bmatrix}\begin{bmatrix} x_{a}\\ y_{a}\\ z_{a}\\ s_{a} \end{bmatrix} \\ = L(q_{a})q_{b} = \begin{bmatrix} s_{a} & -z_{a} & y_{a} & x_{a}\\ z_{a} & s_{a} & -x_{a} & y_{a}\\ -y_{a}& x_{a} & s_{a} & z_{a}\\ -x_{a}& -y_{a} & -z_{a} & s_{a} \end{bmatrix}\begin{bmatrix} x_{b}\\ y_{b}\\ z_{b}\\ s_{b} \end{bmatrix}$
为了简化，令 $q=[x \ y \ z \ s] = [w \ s]$, 则有：
$R(q) = \Omega(w)+sI_{4\times4} = \begin{bmatrix} -[w]_{\times} & w\\ -w^{T}& 0 \end{bmatrix} + sI_{4\times4}$ $L(q) = \Psi(w)+sI_{4\times4} = \begin{bmatrix} [w]_{\times} & w\\ -w^{T}& 0 \end{bmatrix} + sI_{4\times4}$
对于四元素的求导，我们定义 $q_{t}$为 $t$时刻下的单位四元素， $w$为 $q_{t}$确定的角速度，则关于 $q_{t}$的导数为： $\dot{q}_{t} = \frac{1}{2} \begin{bmatrix} -[w]_{\times} & w\\ -w^{T}& 0 \end{bmatrix}q_{t} = \frac{1}{2}\Omega(w)q_{t}=\frac{1}{2}R(\begin{bmatrix} w\\ 0 \end{bmatrix})q_{t} = \frac{1}{2}q_{t} \otimes \begin{bmatrix} w\\ 0 \end{bmatrix}$

因此对于IMU连续形式下的旋转状态(用四元素表示)推导，我们有：
$q_{b_{k+1}^{w}}=q_{b_{k}}^{w} \otimes q_{b_{k+1}}^{b_{k}} = q_{b_{k}}^{w} \otimes \int _{t\in [t_{k}, t_{k+1}]} \dot{q_{t}^{b_{k}}} dt = q_{bk}^{w} \otimes \int_{t\in[t_{k}, t_{k+1}]} \frac{1}{2} q_{t}^{b_{k}}\otimes \begin{bmatrix} w_{t}^{b_{k}}\\ 0\end{bmatrix}dt \\ =q_{b_{k}}^{w} \otimes \int_{t \in [t_{k}, t_{k+1}]} \frac{1}{2}q_{t}^{b_{k}} \otimes \begin{bmatrix} \hat{w_{t}}-b_{wt}-n_{w}\\ 0\end{bmatrix} dt \\ = = q_{bk} \otimes \int_{t\in[t_{k}, t_{k+1}]} \frac{1}{2} \Omega (\hat{w}_{t}-b_{wt}-n_{w})q_{t}^{bk}dt$

---

3.2 离散形式下的IMU运动模型
3.2.1 欧拉法
使用欧拉法，即 $k+1$时刻的位姿是用第 $k$时刻的测量值 $\hat{a}_{b_{k}}$, $\hat{w}_{b_{k}}$来计算的：
$p^{w}_{b_{k+1}} = p_{b_{k}}^{w} + v_{b_{k}}^{w} \Delta t_{k} + \frac{1}{2}\hat{a}_{b_{k}}\delta t^{2}$ $v_{b_{k+1}}^{w} = v_{b_{k}}^{w} + \hat{a}_{b_{k}} \delta t$ $q^{w}_{b_{k+1}} = q^{w}_{b_{k}} \otimes \begin{bmatrix} 1\\ \frac{1}{2}\hat{w}_{b_{k}}\delta t \end{bmatrix}$ 其中 $\hat{a}_{b_{k}} = q_{b_{k}}^{w}(a_{b_{k}}-b_{ak})-g^{w}$ $\hat{w}_{b_{k}} = w_{b_{k}}-b_{wk}$

3.2.2 中值法
使用中值法，即 $k+1$时刻的位姿是用俩个时刻 $k$和 $k+1$测量值 $a$, $w$的平均值来计算的：
$p^{w}_{b_{k+1}} = p_{b_{k}}^{w} + v_{b_{k}}^{w} \Delta t_{k} + \frac{1}{2}\bar{\hat{a}}_{t}\delta t^{2}$ $v_{b_{k+1}}^{w} = v_{b_{k}}^{w} + \bar{\hat{a}}_{t} \delta t$ $q^{w}_{b_{k+1}} = q^{w}_{b_{k}} \otimes \begin{bmatrix} 1\\ \frac{1}{2}\bar{\hat{w}}_{t}\delta t \end{bmatrix}$ 其中 $\bar{\hat{a}}_{t} = \frac{1}{2}[q_{b_{k}}^{w}(a_{b_{k}}-b_{ak})-g^{w} + q_{b_{k+1}}^{w}(a_{b_{k+1}}-b_{ak+1})-g^{w}]$ $\bar{\hat{w}}_{t} = \frac{1}{2}(w_{b_{k}}-b_{wk}+w_{b_{k+1}}-b_{wk+1})$ 假设在短时间内加速度计和陀螺仪的偏置不变，则有： $b_{ak}=b_{ak+1}, \ b_{wk} = b_{wk+1}$

4.IMU预积分 (基于第K帧IMU body坐标系下的运动模型)

通过公式 $(1)$可以看到，IMU 的积分需要依赖与第 $k$ 帧的 $v$ 和 $R$ (基于世界坐标系下的)，当我们在后端进行非线性优化时，需要迭代更新第 $k$ 帧的 $v$ 和 $R$，这将导致我们需要根据每次迭代后的值重新进行积分，这将非常耗时。我们考虑将优化变量从第 $k$ 帧到第 $k+1$ 帧的 IMU 积分项中分离开来。

4.1 连续形式下的IMU运动模型
IMU预积分的思想就是将参考坐标系从世界坐标系 $w$调整为第 $k$帧的IMU body坐标系 $b_{k}$下，可通过在等式俩端同时乘以 $R^{b_{k}}_{w}$得到：【论文式[5][6]】
$R^{b_{k}}_{w}p^{w}_{b_{k+1}}=R^{b_{k}}_{w}(p_{b_{k}}^{w}+v^{w}_{b_{k}}\Delta t_{k}-\frac{1}{2}g^{w}\Delta t_{k}^{2}) + \alpha^{b_{k}}_{b_{k+1}}$ $R^{b_{k}}_{w}v_{b_{k+1}}^{w} = R_{w}^{b_{k}}(v_{b_{k}}^{w}-g^{w}\Delta t_{k})+\beta^{b_{k}}_{b_{k+1}}$ $q_{w}^{b_{k}} \otimes q_{b_{k+1}}^{w} = \gamma _{b_{k+1}} ^{b_{k}}$
其中 $\alpha^{b_{k}}_{b_{k+1}} = \int \int _{t\in [t_{k}, t_{k+1}]} R_{t}^{b_{k}} (\hat{a}_{t}-b_{at}-n_{a}) dt^{2}$ $\beta_{b_{k+1}}^{b_{k}} = \int _{t\in [t_{k}, t_{k+1}]}R_{t}^{b_{k}}(\hat{a}_{t}-b_{at}-n_{a})dt$ $\gamma_{b_{k+1}} = \int _{t \in [t_{k}, t_{k+1}]} \frac{1}{2} \Omega(\hat{w}_{t}-b_{wt}-n_{w}) \gamma_{t}^{b_{k}}dt$

此时的积分结果 $\alpha^{b_{k}}_{b_{k+1}}$、 $\beta^{b_{k}}_{b_{k+1}}$、 $\gamma^{b_{k}}_{b_{k+1}}$可以理解为 $b_{k+1}$对 $b_{k}$的相对运动量， $b_{k}$的状态并不会对其产生影响，因此将其作为非线性优化变量，可以避免状态的重复传递。

注意，这是在假设IMU偏置 $b_{a}$、 $b_{w}$已经确定的情况下，实际上偏置也是需要优化的变量，那么每次迭代时， $b_{a}$、 $b_{w}$发生改变，得重新根据公式求得所有帧之间的IMU预积分。

当偏置变换很小时，可以将 $\alpha_{b_{k+1}}^{b_{k}}$、 $\beta_{b_{k+1}}^{b_{k}}$、 $\gamma_{b_{k+1}}^{b_{k}}$按其偏置的一阶近似来调整，否则就进行重新传递。【论文式[12]】(这部分只是抛出一个概念，后面会讲为什么这样写)
$\alpha_{b_{k+1}}^{b_{k}} \approx \hat{\alpha}_{b_{k+1}}^{b_{k}} + J_{b_{a}}^{ \alpha} \delta b_{a} + J_{b_{w}}^{ \alpha} \delta b_{w}$ $\beta_{b_{k+1}}^{b_{k}} \approx \hat{\beta}_{b_{k+1}}^{b_{k}} + J_{b_{a}}^{ \beta} \delta b_{a} + J_{b_{w}}^{ \beta} \delta b_{w}$ $\gamma_{b_{k+1}}^{b_{k}} \approx \hat{\gamma}_{b_{k+1}}^{b_{k}} \begin{bmatrix} 1 \\ \frac{1}{2}J_{b_{w}}^{\gamma}\delta b_{w} \end{bmatrix}$

4.2 离散形式下的IMU运动模型
4.2.1 两帧之间 PVQ 增量的欧拉法离散形式
欧拉法给出第i时刻与第i+1时刻的预积分量估计值的关系： 【论文式[7]】
$\hat{\alpha}^{b_{k}}_{i+1} = \hat{\alpha}^{b_{k}}_{i} + \hat{\beta}_{i}^{b_{k}}\delta t + \frac{1}{2} R(\hat{\gamma}_{i}^{b_{k}})(\hat{a}_{i}-b_{ai})\delta t^{2}$ $\hat{\beta}^{b_{k}}_{i+1} = \hat{\beta}^{b_{k}}_{i} + \frac{1}{2} R(\hat{\gamma}_{i}^{b_{k}})(\hat{a}_{i}-b_{ai})\delta t$ $\hat{\gamma}^{b_{k}}_{i+1} = \hat{\gamma}^{b_{k}}_{i} \otimes \hat{\gamma}^{i}_{i+1} = \hat{\gamma}^{b_{k}}_{i} \otimes \begin{bmatrix} 1\\ \frac{1}{2}(\hat{w}_{i}-b_{wi})\delta t \end{bmatrix}$
其中 $i$是 $[t_{k}, t_{k+1}]$对应的离散时间

4.2.2 两帧之间 PVQ 增量的中值法离散形式
代码中采用的基于中值法的 IMU 预积分公式，这在Estimator::processIMU()函数 和IntegrationBase::push_back()函数中得以实现，注意这里积分出来的是前后两帧之间的 IMU 增量信息。
$\hat{\alpha}^{b_{k}}_{i+1} = \hat{\alpha}^{b_{k}}_{i} + \hat{\beta}_{i}^{b_{k}}\delta t+ \frac{1}{2} \bar{\hat{a}}_{i}\delta t^{2}$ $\hat{\beta}^{b_{k}}_{i+1} = \hat{\beta}^{b_{k}}_{i} + \frac{1}{2} \bar{\hat{a}}_{i}\delta t$ $\hat{\gamma}^{b_{k}}_{i+1} = \hat{\gamma}^{b_{k}}_{i} \otimes \hat{\gamma}^{i}_{i+1} = \hat{\gamma}^{b_{k}}_{i} \otimes \begin{bmatrix} 1\\ \frac{1}{2} \bar{\hat{w}}_{i}\delta t \end{bmatrix}$ 其中 $\bar{\hat{a}}_{t} = \frac{1}{2}[q_{i}(\hat{a}_{i}-b_{i}) + q_{i+1}(\hat{a}_{i+1}-b_{ai})]$ $\bar{\hat{w}}_{i} = \frac{1}{2}(\hat w_{i} + \hat w_{i+1})-b_{wi}$
初始状态下 $\alpha_{b_{k}}^{b_{k}}$、 $\beta_{b_{k}}^{b_{k}}$为0, $\gamma_{b_{k}}^{b_{k}}$为单位四元素， $n_{a}$、 $n_{w}$被视为0， $i$为在 $[k, k+1]$中IMU测量值的某一时刻， $\delta t$为IMU测量值 $i$和 $i+1$之间的时间间隔。

5. PVQ增量的误差递推方程、协方差及雅克比矩阵

---

5.1 一个IMU数据作为测量值的噪声协方差我们能够标定，一段时间内多个IMU数据积分形成的预积分量的协方差如何计算？

要推导预积分量的协方差，需要知道IMU噪声和预积分量之间的线性递推关系。

假设已知了相邻时刻误差的线性传递方程：
$\eta_{ik+1} = F_{k}\eta_{ik} + G_{k}n_{k}$其中 $\eta_{ik}$为状态量误差且 $\eta_{ik}=[\delta\theta_{ik}, \delta v_{ik}, \delta p_{ik}]$， $n_{k}$为测量噪声且 $n_{k}=[n_{k}^{g}, n_{k}^{g}]$。
可以看出误差的传递由倆部分组成：当前时刻的误差传递给下一时刻，当前时刻测量噪声传递给下一时刻。

5.2 如何实现非线性方程的递推方程？
通常对于状态量之间的递推关系是非线性的方程如 $x_{k+1} = f(x_{k}, u_{k})$，其中状态量 $x$、 $u$为系统的输入量。

可以用俩种方法来推导状态误差传递的线性递推关系：

• 一种是基于一阶泰勒展开的误差递推方程
• 一种是基于误差随时间变化的递推方程 (是基于误差随时间变化来推导的)

5.2.1 基于一阶泰勒展开的误差递推方程

---