一、鸢尾花数据集
Iris 鸢尾花数据集内包含 3 类分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica),共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。
使用时可通过外部数据文件导入,也可通过 sklean.datasets库导入实现。
二、三种梯度下降实现一元线性回归----花瓣长度和花瓣宽度
1、批量梯度下降
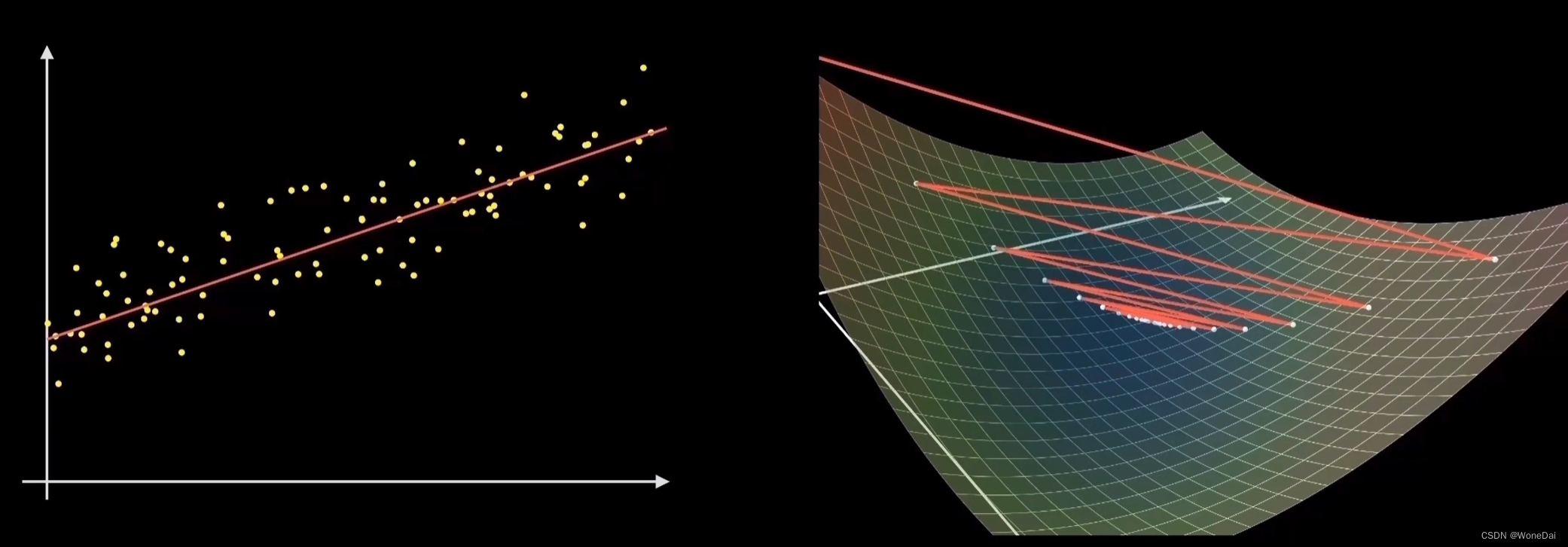
批量梯度下降法是最原始的形式,它是指在每一次迭代时使用所有样本来进行梯度的更新。
优点:
(1)一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
(2)由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点:
(1)当样本数目 m 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X = iris.data[:, 2] # 取花瓣长度特征
y = iris.data[:, 3]
# 数据标准化
'''
即将数据集中每个特征的值都减去该特征的均值,然后再除以该特征的标准差,使得每个特征的值都在均值为0,方差为1的范围内。
这种数据处理方式能够加速训练过程并提高模型的准确性,
因为在使用梯度下降等优化算法时,数据集中不同特征的值范围过大会导致梯度下降过程中每个特征的权重更新速度不同,
从而导致优化效果较差。标准化处理能够将不同特征的值范围缩小到相近的范围,避免这个问题。
'''
X = (X - np.mean(X)) / np.std(X)
# 构建模型
theta = np.zeros(2) # 参数初始化
alpha = 0.01 # 学习率
iters = 1000 # 迭代次数
m = len(X) # 样本数量
# 批量梯度下降算法
def bgd(X, y, theta, alpha, iters):
J_history = [] # 记录代价函数的值
for i in range(iters):
h = np.dot(X, theta) # 预测值
error = h - y # 误差
cost = 1 / (2 * m) * np.dot(error.T, error) # 计算代价函数
J_history.append(cost)
theta = theta - (alpha / m) * np.dot(X.T, error) # 更新参数
return theta, J_history
# 训练模型
'''
在线性回归中,我们通常要在数据中增加一列全为1的特征,作为常数项的系数,也就是截距(intercept)。
这是因为线性回归模型是一个零点穿越的模型,即当特征取值为0时,模型的预测值也应该为0。
而这个零点交叉的地方,就是截距的取值。因此,在模型中加入截距这一项,可以更好地对数据进行拟合。
'''
X = np.c_[np.ones(m), X] # 增加一列全为1的特征
theta, J_history = bgd(X, y, theta, alpha, iters)
print("theta: ", theta)
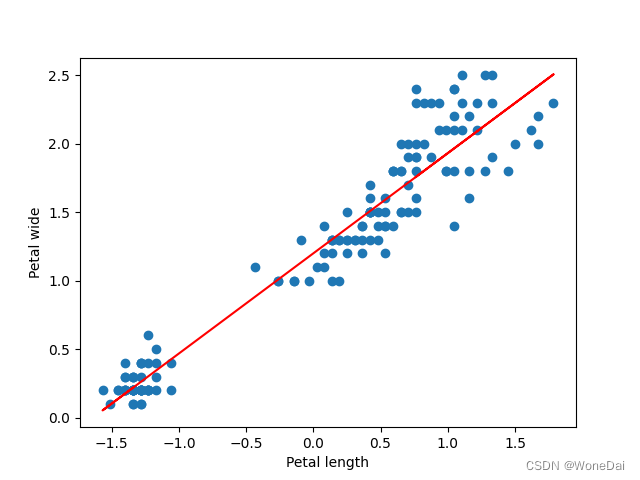
# 可视化
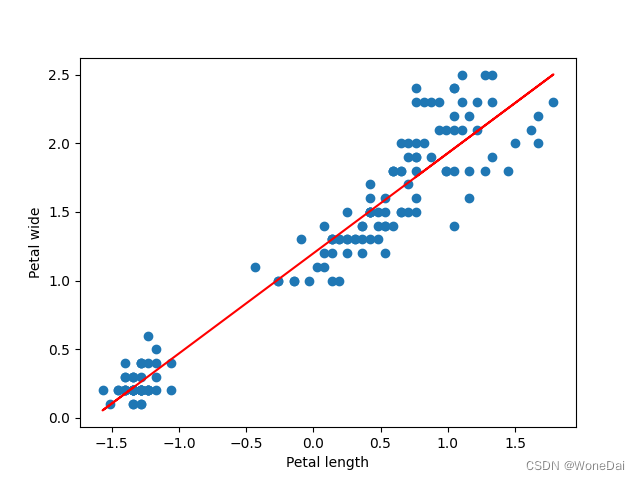
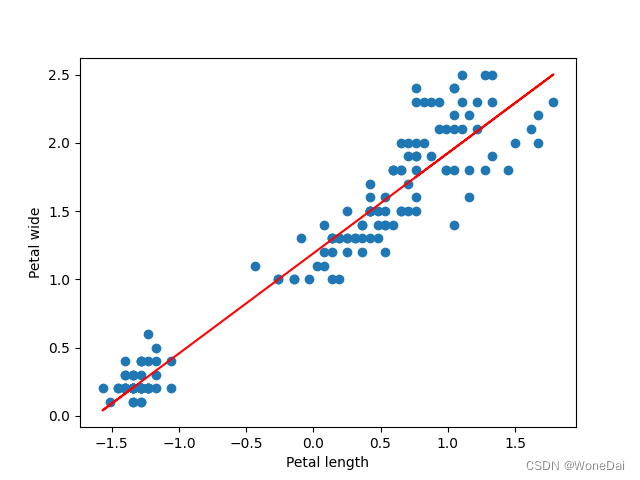
plt.scatter(X[:, 1], y)
plt.plot(X[:, 1], np.dot(X, theta), color='r')
plt.xlabel('Petal length')
plt.ylabel('Petal wide')
plt.show()
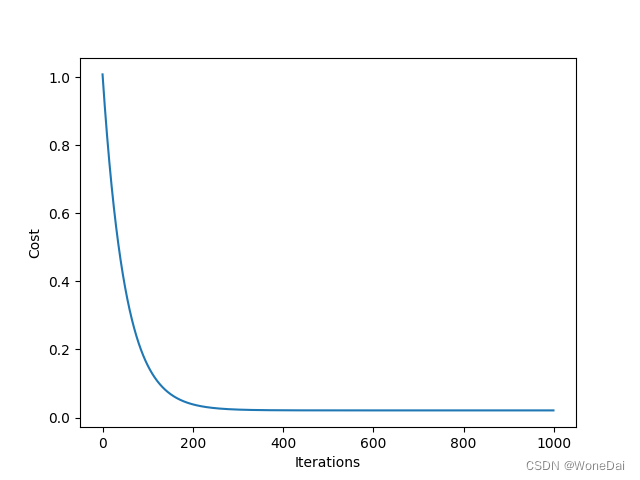
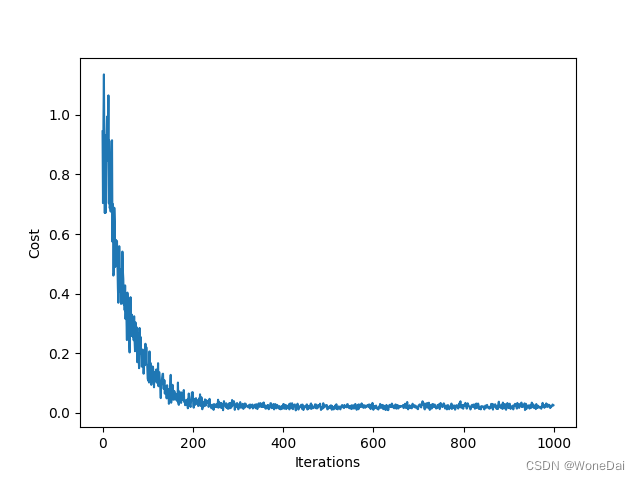
# 绘制代价函数随迭代次数变化的曲线
plt.plot(np.arange(iters), J_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.show()
2、小批量梯度下降
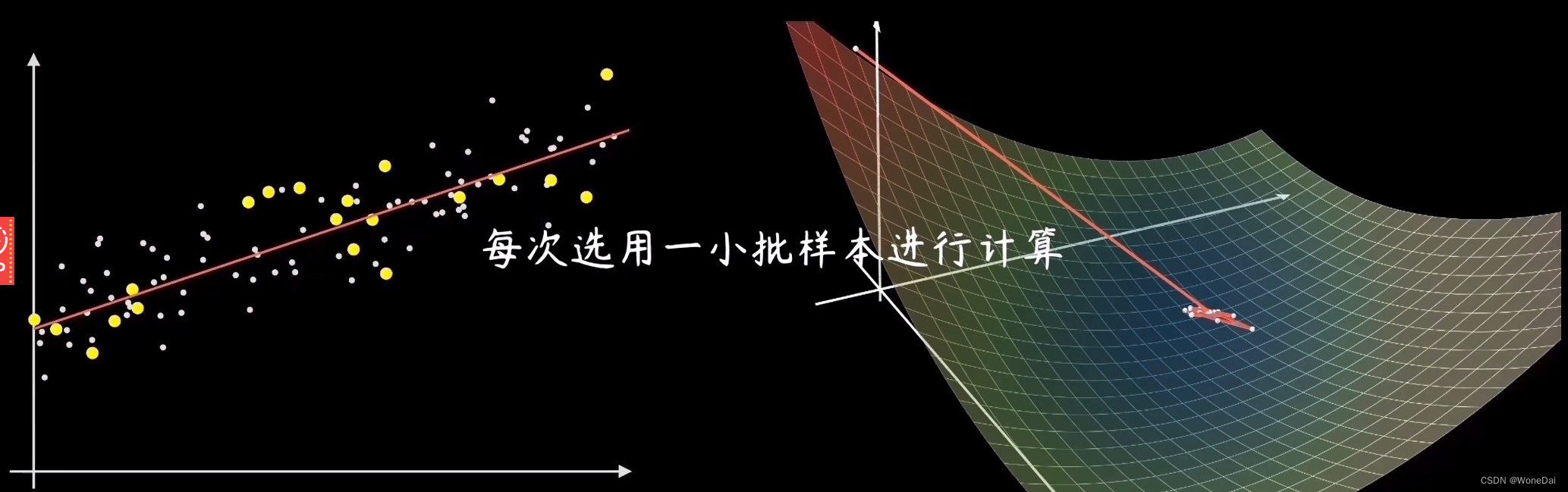
小批量梯度下降,是对批量梯度下降以及随机梯度下降的一个折中办法。
其思想是:每次迭代 使用 '' batch_size'' 个样本来对参数进行更新。
优点:
(1)通过矩阵运算,每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
(2)每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。
(3)可实现并行化。
缺点:
(1)batch_size的不当选择可能会带来一些问题。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X = iris.data[:, 2] # 取花瓣长度特征
y = iris.data[:, 3]
# 数据标准化
X = (X - np.mean(X)) / np.std(X)
# 构建模型
theta = np.zeros(2) # 参数初始化
alpha = 0.01 # 学习率
iters = 1000 # 迭代次数
batch_size = 16 # 小批量大小
m = len(X) # 样本数量
# 小批量梯度下降算法
def mini_batch_gd(X, y, theta, alpha, iters, batch_size):
J_history = [] # 记录代价函数的值
for i in range(iters):
# 从样本中随机选择一个小批量
'''
np.random.choice(m, batch_size, replace=False) 是用来随机抽取 batch_size 个数的函数,
其中 m 表示总共的样本数,batch_size 表示每次迭代随机抽取的样本数,
replace=False 表示不可重复抽取,即每次抽取的样本都是不同的。这里将随机抽取的样本的索引存储在 idx 变量中。
'''
idx = np.random.choice(m, batch_size, replace=False)
X_batch = X[idx]
y_batch = y[idx]
h = np.dot(X_batch, theta) # 预测值
error = h - y_batch # 误差
cost = 1 / (2 * batch_size) * np.dot(error.T, error) # 计算代价函数
J_history.append(cost)
theta = theta - (alpha / batch_size) * np.dot(X_batch.T, error) # 更新参数
return theta, J_history
# 训练模型
X = np.c_[np.ones(m), X] # 增加一列全为1的特征
theta, J_history = mini_batch_gd(X, y, theta, alpha, iters, batch_size)
print("theta: ", theta)
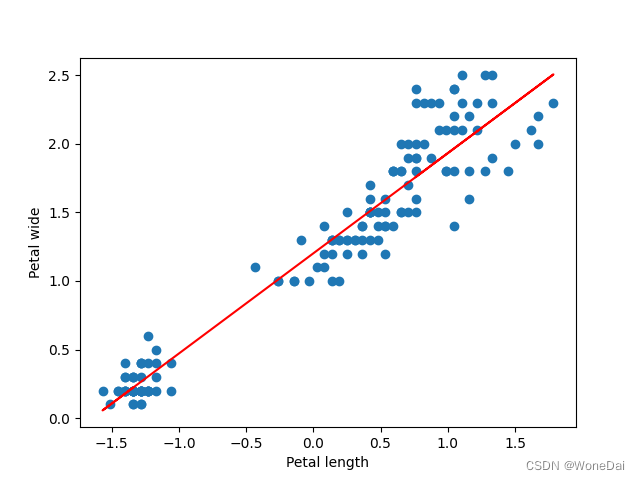
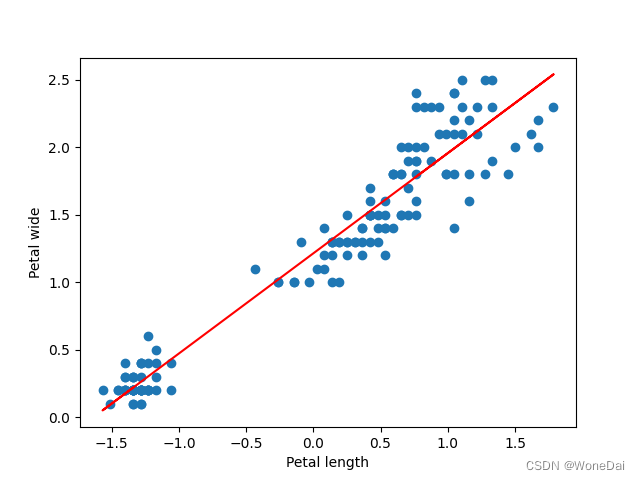
# 可视化
plt.scatter(X[:, 1], y)
plt.plot(X[:, 1], np.dot(X, theta), color='r')
plt.xlabel('Petal length')
plt.ylabel('Petal wide')
plt.show()
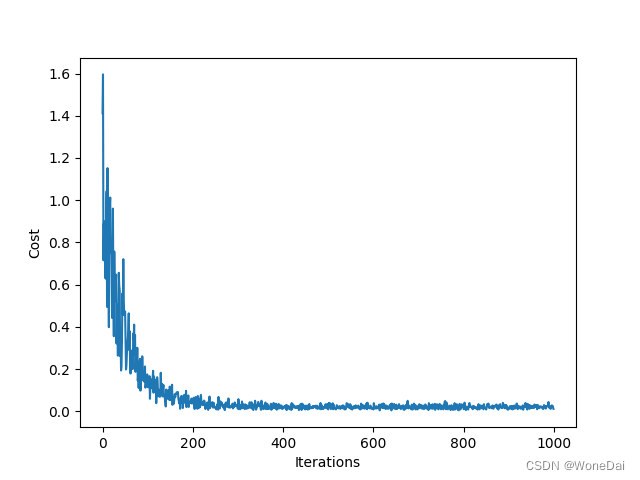
# 绘制代价函数随迭代次数变化的曲线
plt.plot(np.arange(iters), J_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.show()
3、随机梯度下降
随机梯度下降法不同于批量梯度下降,随机梯度下降是每次迭代使用一个样本来对参数进行更新。
优点:
(1)由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
(1)准确度下降。即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线收敛。
(2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X = iris.data[:, 2] # 取花瓣长度特征
y = iris.data[:, 3]
# 数据标准化
X = (X - np.mean(X)) / np.std(X)
# 构建模型
theta = np.zeros(2) # 参数初始化
alpha = 0.01 # 学习率
iters = 1000 # 迭代次数
m = len(X) # 样本数量
# 随机梯度下降算法
def sgd(X, y, theta, alpha, iters):
J_history = [] # 记录代价函数的值
for i in range(iters):
# 随机选择一个样本
random_index = np.random.randint(0, m)
xi = X[random_index, :]
yi = y[random_index]
# 预测值
h = np.dot(xi, theta)
error = h - yi # 误差
'''
在批量梯度下降中,每一次更新参数都需要遍历整个数据集,
因此计算代价函数时直接使用整个数据集的误差平方和即可。
而在小批量或随机梯度下降中,只是使用部分数据集来更新参数,因此计算代价函数时只能使用部分数据集的误差平方和。
'''
cost = 1 / 2 * (error ** 2) # 计算代价函数
J_history.append(cost)
# 更新参数
theta = theta - alpha * error * xi.T
return theta, J_history
# 训练模型
X = np.c_[np.ones(m), X] # 增加一列全为1的特征
theta, J_history = sgd(X, y, theta, alpha, iters)
print("theta: ", theta)
# 可视化
plt.scatter(X[:, 1], y)
plt.plot(X[:, 1], np.dot(X, theta), color='r')
plt.xlabel('Petal length')
plt.ylabel('Petal wide')
plt.show()
# 绘制代价函数随迭代次数变化的曲线
plt.plot(np.arange(iters), J_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.show()
三、回归结果和Loss变化体现
1、批量梯度下降
alpha = 0.01 # 学习率 iters = 1000 # 迭代次数 theta: [1.19927891 0.73144858]
2、小批量梯度下降
alpha = 0.01 # 学习率 iters = 1000 # 迭代次数 batch_size = 16 # 小批量大小 theta: [1.2015789 0.73079877]
alpha = 0.01 # 学习率 iters = 1000 # 迭代次数 batch_size = 26 # 小批量大小 theta: [1.19859429 0.72959769]
3、随机梯度下降
alpha = 0.01 # 学习率 iters = 1000 # 迭代次数 theta: [1.21414173 0.74142117]
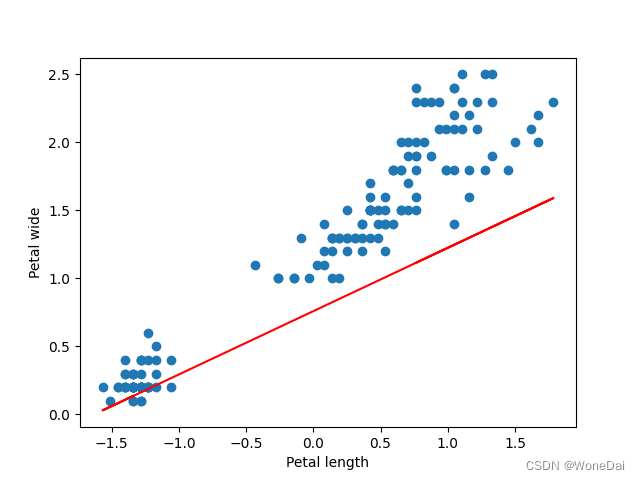
alpha = 0.001 # 学习率 iters = 1000 # 迭代次数 theta: [0.75929483 0.4656095]
alpha = 0.01 # 学习率 iters = 10000 # 迭代次数 theta: [1.19015919 0.73407146]
四、总结
在这个问题中,我们使用了相同的数据集、模型和参数,但是使用了不同的优化算法,包括批量梯度下降(BGD)、小批量梯度下降(MBGD)和随机梯度下降(SGD),下面我们来分析它们的差异。
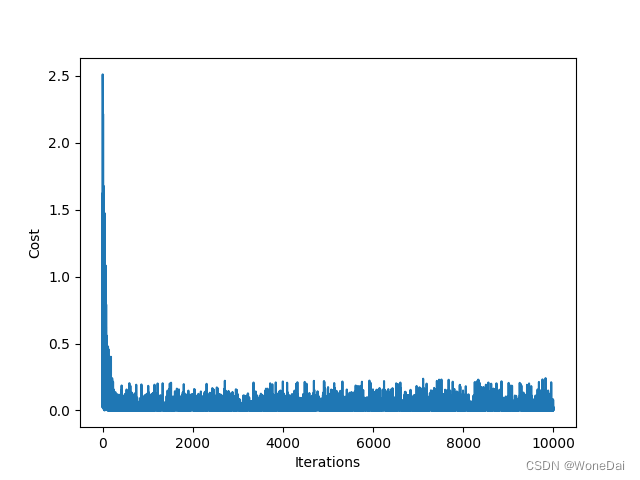
BGD的结果是,1000次迭代,代价函数随迭代次数的变化曲线呈现出单调下降的趋势。
MBGD的结果是,1000次迭代,代价函数随迭代次数的变化曲线呈现出波动性下降的趋势。
SGD的结果是,1000次迭代,代价函数随迭代次数的变化曲线呈现出波动性下降的趋势。
从结果可以看出,三种优化算法都能够在一定程度上优化模型的表现,但它们的优化效果和特点有所不同。首先,BGD是一种每次都遍历所有样本的算法,因此,每一次迭代都需要计算所有样本的代价函数和梯度,计算量较大,但是每次迭代可以朝着最优方向前进。
其次,MBGD是一种每次随机选择一部分样本进行计算的算法,因此,它比BGD更快,而且仍然可以达到最优解,但是它的迭代过程可能会有波动,这是由于选择的样本不同。
最后,SGD是一种每次随机选择一个样本进行计算的算法,它比MBGD更快,但是迭代过程中的波动可能更大。此外,由于每次迭代只计算一个样本,因此SGD比MBGD更容易收敛到局部最优解而不是全局最优解。