Tensor Distance Based Multilinear Locality-Preserved Maximum Information Embedding
基于张量距离的多线性局部保持最大信息嵌入
摘要:本文提出了一种基于张量的降维(dimensionality reduction,DR)统一框架,该框架采用了一种新的张量距离(tensor distance,TD)度量和一种新的多线性局部保持最大信息嵌入(multilinear locality-preserved maximum information embedding,MLPMIE)算法。与传统的受正交性假设约束的欧氏距离不同,TD通过考虑不同坐标之间的关系来度量数据点之间的距离。为了在低维空间中保持自然张量结构,MLPMIE直接处理输入数据的高阶形式,并迭代学习变换矩阵。为了保持局部几何结构,同时最大化全局分辨力,MLPMIE将局部和全局结构保持在流形模型中。通过将TD集成到张量嵌入中,TD-MLPMIE在整个学习过程中执行基于张量的DR,并在各种标准数据集上实现稳定的性能改进。
Introduce
模式分析任务通常具有高维特征空间,这导致识别精度低和计算成本高。降维(DR)技术通过为给定的观测值和目标生成原始特征空间的低维等价,提供了一种解决这一问题的方法。
然而,传统的DR算法在嵌入之前将输入数据展开为向量,即使数据自然是高阶张量。这种矢量化大大增加了数据分析的计算成本,严重破坏了高阶数据固有的张量结构。为了解决这些问题,Vasilescu和Terzopoulos在DR中引入了多线性代数来进行高阶数据分析。从那时起,许多多线性DR技术,也称为基于张量的DR技术,被提出。典型的多线性DR算法包括多线性主成分分析(MPCA)、多线性判别分析(MLDA)、多线性独立成分分析、张量子空间分析、基于张量的局部保持投影(TLPP)、张量线性拉普拉斯判别等。
现有的大多数基于张量的技术旨在保留高阶数据之间的关系,这些关系通常由不同数据点之间的距离来衡量。因此,基于张量的DR的性能不仅取决于嵌入策略,还与距离度量密切相关。当前基于张量的技术只是使用欧几里德距离来度量不同数据点之间的关系。然而,在欧几里德空间中,高阶数据点X由坐标x1、x2、。对应数轴e1、e2、,式中(ei,ej)=0(i?=j)。这意味着假设欧氏空间中的任意两个基ei和ej相互垂直,因此坐标xi和xj相互独立。不幸的是,这种正交性假设忽略了高阶数据的不同坐标之间的关系,例如图像中像素的空间关系,从而限制了进一步基于张量的嵌入的性能。
为了解除这种正交性假设,**我们提出了一种新的张量距离(TD)度量来度量高阶数据点之间的关系。**基于这个距离度量,我们进一步提出了一个统一的DR框架,称为基于TD的多线性局部保持最大信息嵌入(TD-MLPMIE),根据一种基于向量的算法称为局部保持最大信息投影(LPMIP)[19]。TD-MLPMIE继承了LPMIP的特性,通过在流形模型中同时平衡局部内部和局部之间,保持局部几何结构并最大化全局区分。此外,作为一种多线性技术,TD-MLPMIE在降低计算复杂性的同时提高了数据分析的准确性。
本文的其余部分组织如下。第二节提出了TD指标。第三节介绍TD-MLPMIE。第四节对所提出的方法进行了理论分析。第五节报告了实验结果。本文在第六节得出结论。
张量距离
对于某些类型的高阶数据,由于前面讨论的正交性假设,传统的欧氏距离可能无法反映两个数据点之间的实际距离。在本节中,我们提出了一种称为TD的新距离度量,用于建模任意阶数数据的不同坐标之间的相关性。
给定数据点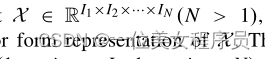
我们用x来表示X的向量形式表示,因此,X中的元素
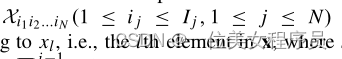
对应于xl,即x中的第l个元素,其中l=i1+
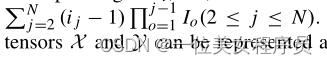
那么两个张量X和Y之间的TD可以表示为
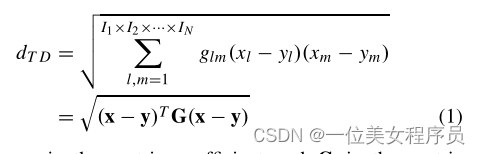
其中glm是度量系数,G是度量矩阵。为了反映高阶数据不同坐标之间的内在关系,一个自然的考虑是度量系数应与元素距离相关。Wang等人已经证明,对于图像数据,即二阶张量,如果度量系数适当地依赖于像素位置的距离,则获得的距离度量可以有效地反映像素之间的空间关系。受本文启发,我们设计了以下度量矩阵G:
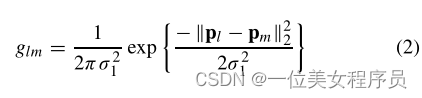
其中σ1是正则化参数,||pl − pm||2是Xi1i2…in(对应于xl)和Xi1’i2’…in’(对应于xm)之间的位置距离,定义为
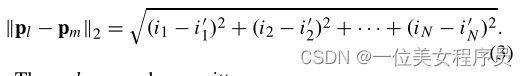
然后,dTD可以重写为
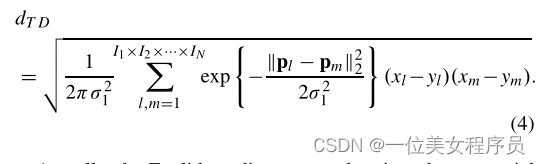
实际上,欧几里德距离可以看作是拟议TD的一个特例。如果我们将度量矩阵设为单位矩阵,即G=i,这意味着我们只考虑张量空间中两个高阶数据的对应坐标之间的距离,那么TD将缩减为欧氏距离。
由于G是实对称正定矩阵,我们可以很容易地将其分解如下:
 其中G(1/2)也是一个实对称矩阵,定义为
其中G(1/2)也是一个实对称矩阵,定义为
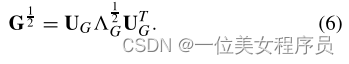
这里,AG是一个对角线矩阵,其元素是G的特征值,UG是一个正交矩阵,其列向量是G的特征向量。将变换G1/2应用于向量形式表示x和y,i。ex’=G 1/2x,y’=G 1/2y,然后将x和y之间的TD减少到x’和y’之间的传统欧氏距离
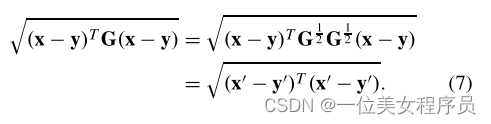
因此,很容易将TD嵌入到一般的学习过程中,我们只需对原始数据执行转换G1/2,然后在以下过程中使用转换后的数据
基于张量距离的多线性局部保持最大信息嵌入
基于新的距离度量TD,我们根据基于向量的方法LPMIP,提出了一种新的DR方法TD-MLPMIE