Tensor Distance based Multilinear Multidimensional Scaling for Image and Video Analysis

Tensor Distance based Multilinear Multidimensional Scaling for Image and Video Analysis
基于张量距离的多线性多维尺度图像和视频分析

摘要

提出了一种基于张量距离的多线性多维尺度降维技术（TD-MMDS）。首先，我们提出了一种新的距离度量，称为张量距离（TD），用于构建高阶数据点的关系图。然后，我们采用迭代策略顺序学习变换矩阵，以最好地保持低维嵌入空间中高阶数据的成对TDs。TD-MMDS通过结合张量距离和张量嵌入，提供了一个统一的基于张量的降维框架，在整个学习过程中保持了高阶数据的固有结构。在标准图像和视频数据集上的实验验证了TD-MMDS的有效性。

Introduction

图像和视频分析经常会遇到特征空间维数巨大的问题。降维技术通过为给定目标生成原始特征空间的低维等价来解决这一问题。然而，传统的降维算法通常将输入数据展开为向量形式，即使数据自然是高阶张量。这种矢量化大大增加了数据分析的计算量，严重破坏了高阶数据固有的张量结构。
为了解决矢量化带来的问题，人们提出了一些基于张量的降维技术，如张量主成分分析（tensor principal component analysis，TPCA）和张量线性判别分析（tensor linear discriminant analysis，TLDA）。这些算法旨在通过顺序学习变换矩阵来保持高阶数据之间的关系，高阶数据通常使用数据点之间的距离来测量。因此，基于张量的维数约简的性能不仅取决于嵌入策略，而且与距离度量密切相关。目前，基于张量的技术只是利用传统的欧几里德距离作为距离度量。在欧几里德空间中，空间R^I1xI2…In.中的高阶数据X可以由具有相应基e1,e2,…,eI1xI2x…In的坐标X1,X2,…,XI1xI2x…In表示，其中<ei，ej>=0（i≠ j） 。这意味着任意两个基ei，ej都假定相互垂直，因此任何坐标xi都是相互独立的。然而，这种正交性假设忽略了高阶数据的不同坐标之间的关系，例如图像中像素的空间关系，从而限制了进一步张量嵌入的性能。
为了释放当前距离度量的正交性假设，我们提出了一种新的张量距离（TD）来度量高阶数据之间的关系，尤其是图像和视频，这些数据在不同坐标之间具有很强的相关性。然后，我们将一种典型的基于距离保持的降维算法多维缩放（Multidimensional Scaling,MDS）[9]扩展到其多线性版本(Multilinear Multidimensional Scaling,MMDS)。结合TD和MMDS，我们提出了一种新的基于张量距离的多线性多维尺度降维算法（TD-MMDS），该算法在整个学习过程中保持了高阶数据的固有结构。

张量距离

对于某些类型的高阶数据，由于前面讨论的正交性假设，传统的欧氏距离可能无法反映两个数据点之间的实际距离。在本节中，我们提出了一种称为TD的新距离度量，用于建模任意阶数数据的不同坐标之间的相关性。
给定数据点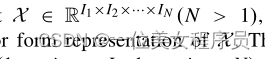
我们用x来表示X的向量形式表示，因此，X中的元素

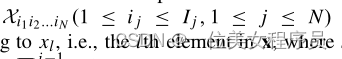
对应于xl，即x中的第l个元素，其中l=i1+

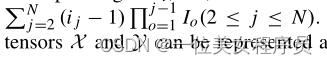
那么两个张量X和Y之间的TD可以表示为

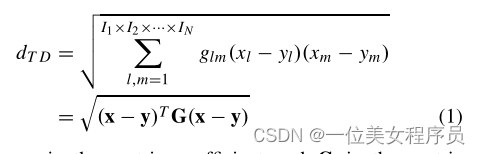
其中glm是度量系数，G是度量矩阵。为了反映高阶数据不同坐标之间的内在关系，一个自然的考虑是度量系数应与元素距离相关。Wang等人已经证明，对于图像数据，即二阶张量，如果度量系数适当地依赖于像素位置的距离，则获得的距离度量可以有效地反映像素之间的空间关系。受本文启发，我们设计了以下度量矩阵G：

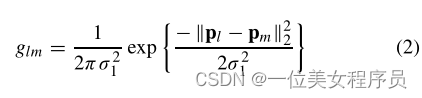
其中σ1是正则化参数，||pl − pm||2是Xi1i2…in（对应于xl）和Xi1’i2’…in’（对应于xm）之间的位置距离，定义为

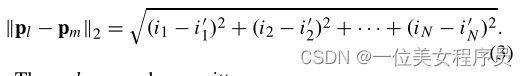
然后，dTD可以重写为

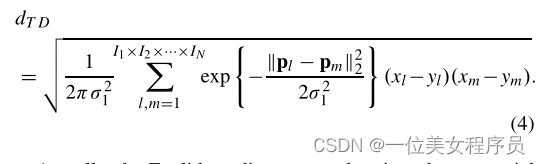
实际上，欧几里德距离可以看作是拟议TD的一个特例。如果我们将度量矩阵设为单位矩阵，即G=i，这意味着我们只考虑张量空间中两个高阶数据的对应坐标之间的距离，那么TD将缩减为欧氏距离。
由于G是实对称正定矩阵，我们可以很容易地将其分解如下：
其中G^(1/2)也是一个实对称矩阵，定义为

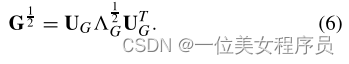
这里，AG是一个对角线矩阵，其元素是G的特征值，UG是一个正交矩阵，其列向量是G的特征向量。将变换G^1/2应用于向量形式表示x和y，i。ex’=G ^1/2x，y’=G ^1/2y，然后将x和y之间的TD减少到x’和y’之间的传统欧氏距离

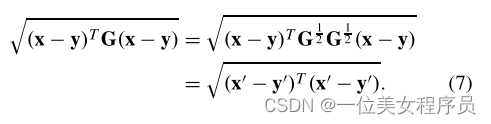
因此，很容易将TD嵌入到一般的学习过程中，我们只需对原始数据执行转换G^1/2，然后在以下过程中使用转换后的数据

基于张量距离的多线性多维尺度

基于张量距离的多线性多维尺度

给定张量空间R^I1xI2x…xIn中的n个数据点X1、X2、…、Xn，无需将输入数据展开为向量形式，基于张量距离的多线性多维缩放（TD-MMDS）旨在找到N个变换矩阵Vk∈R^IkxIk’(Ik’<<Ik,k=1,…,N)，从而通过多线性变换Yj=Xjx1V^T1x2…xnV^TN(j= 1, …, N)获得子空间R^{I1’xI2’x…xIn’}中的n个低维数据点Y1、Y2、…、Yn.
根据图嵌入框架，TD-MMDS的目标函数可以表示为：

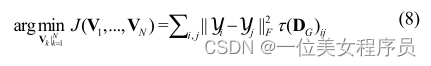
式中，t(DG)=–HSH/2（Sij=d²TD(Xi，Xj)，其中dTD（Xi，Xj）表示两个数据点Xi和Xj之间的张量距离，H=i-（ee^T/n），其中I是单位矩阵，e是所有数据点的向量）。目标函数（8）可以改写为：

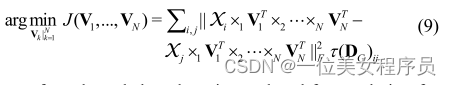
据我们所知，这个高阶非线性规划问题没有封闭形式的解。我们没有直接解决这个问题，而是采用迭代策略[2]、[5]、[6]来寻找局部最优解。在讨论迭代策略之前，我们给出以下定理：
**定理1：**假设V1，V2，…，Vk-1，Vk+1，…，VN是固定的，最小化目标函数J（V1，…，VN）的最优Vk由以下矩阵的第一个Ik′特征向量组成：

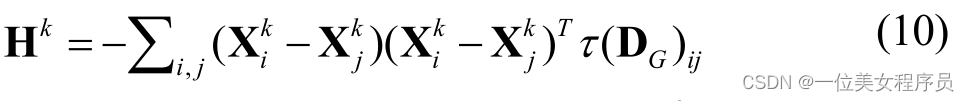
对应于第一个Ik′最大特征值。Xki是张量Xki的k模式展开


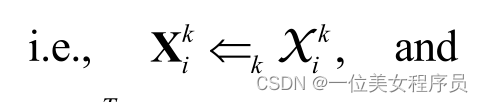
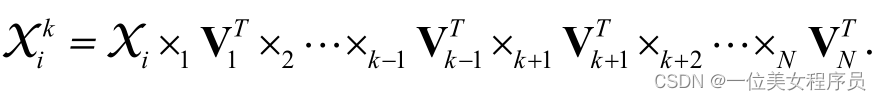
利用多线性代数和矩阵迹的性质可以很容易地证明上述定理。类似的证明可以在[5]和[6]中找到。根据定理1，如果V1，V2，…，Vk-1，Vk+1，…，VN是固定的，则可以通过一个简单的特征分解位置获得最优Vk。因此，迭代策略可以如下所示。首先，我们修正V2，…，VN，并通过最小化目标函数J（V1）获得V1。然后我们固定V1，V3，…，VN，并通过最小化目标函数J（V2）获得最优V2。其余的可以通过类比来推断。最后确定V1，V2，…，VN-1，通过最小化目标函数J（VN）得到最优VN。重复上述步骤，直到满足终止条件，然后我们得到一个解决方案。TD-MMDS的详细过程在算法1中描述。