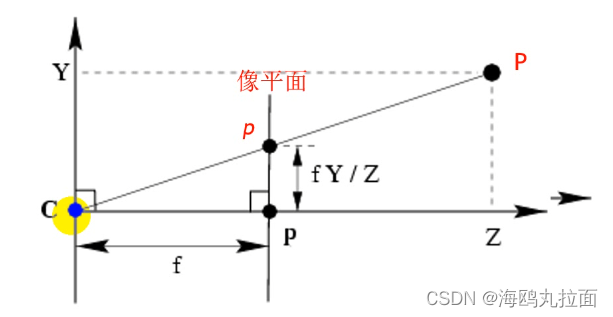

K阵(内部参数矩阵):焦距信息,像主点偏移信息(x0,y0)。
外阵:描述相机拍摄过程中不同位置和姿态信息。由旋转角参数矩阵和位移矩阵组合。

s:畸变参数。
a: 由于生产过程中像素不一定为正方形(长宽比值不同),因此用a表示长宽比值。
图像畸变原因:
- 透镜质量原因
- 光线在远离透镜中心的地方比靠近中心的地方更加弯曲
- 中短焦距:桶状畸变 长焦距:枕型畸变


pitch是围绕X轴旋转,也叫做俯仰角。yaw是围绕Y轴旋转,也叫偏航角。roll是围绕Z轴旋转,也叫翻滚角。
两类参数的总结:

两个矩阵相乘得到三行四列矩阵的过程,完成了空间中的点到图像中点的对应关系。
相机标定中,同步标定内部参数和外部参数,一般包括两种策略:
- 光学标定:利用已知的几何信息(如定长棋盘格)实现参数求解。
- 自标定:在静态场景中利用 structure from motion 估算参数。
标定参数线性回归
通过空间中已知坐标的(特征)点(Xi,Yi,Zi),以及它们在图像中的对应坐标(ui,vi),直接估算11个待求解的内部和外部参数。
u,v是可观测的,X,Y,Z是生产中已知的点信息。
- 最小二乘解:
最小特征值对应的特征向量
- 需要至少6对匹配特征
优点:
- 所有相机参数集中在一个矩阵中,便于求解
- 通过矩阵可以直接描述世界坐标中的三维点,到二维图像平面中点的映射关系
缺点:
- 无法得知具体内参数和外参数
- 求解出的11个未知量,比待定参数(9个)更多、带来了参数不独立/相关的问题
- 对噪声/ 误差敏感
- 高精度的标定板难以制作
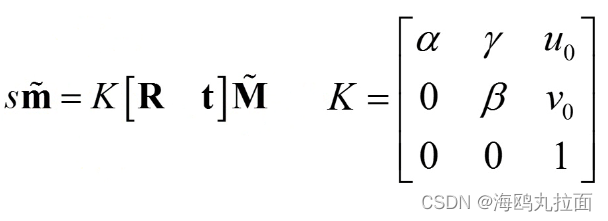
- 2D图像点:
- 3D空间点:
- 齐次坐标:
- 描述空间坐标到图像坐标的映射
- s:世界坐标系到图像坐标系的尺度因子
- K:相机内参矩阵
- (u0,v0):像主点坐标
- α,β:焦距与像素横纵比的融合
- γ:径向畸变参数
张正友标定法:多角度对棋盘格进行拍摄
- 设棋盘格位于Z=0(XOY平面上)
- 定义旋转矩阵R的第i列为
,则有:
- 于是空间到图像的映射可改为:
- 其中H是单应变换Homographic矩阵,可通过最小二乘,从角点世界坐标到图像坐标的关系求解
- H矩阵可以根据特征点/棋盘格角点的空间坐标,以及其图像坐标用最小二乘法很容易求解。
- 令H为H=[h1 h2 h3]
[h1 h2 h3]=λK[r1 r2 t] - Homography有8个自由度
- 由r1和r2正交,且r1和r2的模相等,可以得到如下约束:
正交
模相等
- 定义
- B是对称阵,其未知量可表示为6D向量b
- 设H中的第i列为hi
- 根据b的定义,可以推导出如下公式
- 可以推导出
- 如果有n组观察图像,则v是2n×6的矩阵
Vb = 0 - 根据最小二乘定义,Vb=0的解释
最小特征值对应的特征向量
- 因此,可以直接估算出b,后续可以通过b求解内参
- 当观测平面n≥3时,可以得到b的唯一解
- 当n=2时,一般可令畸变参数γ=0
- 当n=1时,仅能估算出α与β,此时一般可假定像主点坐标u0与v0为0
- B是通过b构造的对称矩阵
- 内部参数可通过如下公式计算(cholesky分解):
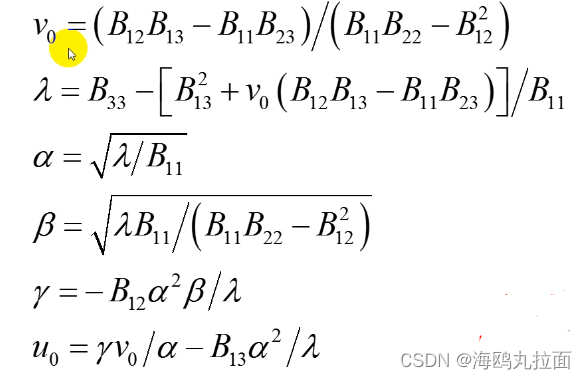
- 外部参数可通过Homography求解,由H=[h1 h2 h3]=λK[r1 r2 t],可推出

- 一般而言,求解出的R=[r1 r2 r3]不会满足正交与归一的标准
- 在实际操作中,R可以通过SVD分解实现规范化
- 给定n张棋盘格图像,每张图像由m个角点
- 最小化下述公式等同于极大似然估计
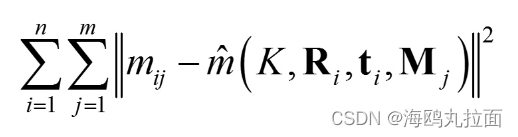
- 上述非线性优化问题可以用Levenberg-Marquardt算法求解
- 需要初值K,
总结:
- 仅需要平面标定板,拍摄若干张图片
- 标定板中的模式十分灵活,可以是棋盘格,也可以是其他几何结构已知的图形
- 实验结果表明张正友标定法具有很好地标定精度