1.搜索算法是一种邻域算法,通常是局部最优点
2.最佳步长沿着可行改进方向最大程度改进目标值,并保持可行的距离
3.梯度信息提供了一个改进方向的代数检验方法
4.凸可行集与线性目标保证了全局最优点
5.3A算法是最基础的搜索算法
上一篇我们介绍了“如何搭建运筹学模型”的核心思想,并介绍了运筹学模型的分类。但没有提及求解模型的方法,今天我们就针对“如何求解运筹学模型”做个综述,以后会针对具体的模型再深入介绍具体的求解方法。
1
DClub选址问题
有数学分析功底的我们知道,一些显式的方程可以得到精确的解,这个我们称为解析方法;但现实中大多数遇到的是无法得到精确解的方程,这时候我们需要用到数值方法。而运筹学模型本质上就是一个优化问题——求解最值模型,因此常常利用数值搜索的方法来求解。
数值搜索,英文是numerical search,思想是依次尝试不同的决策变量取值(即可行解),直到得到一个满意的结果。我们把在当前可行解邻域内对目标值有改进的下一组可行解的迭代过程称为搜索算法(improving search)。换句话说,搜索算法是在当前可行解基础上,通过检查它邻域来寻找比当前更好的解,所谓更好的解,就是对目标有改进的解,并且重复这个过程直到邻域内没有更好的解为止。
注意这里的一个关键词——邻域内。这说明搜索算法得到的是一个局部最优解,这一点我们后面再展开讨论。因此搜索算法又称为局部改进、爬山算法、局部搜索或邻域搜索.
下面我们通过一个例子来详细说明搜索算法的原理——DClub选址问题.
DClub折扣百货商店希望在一个地区新建一个店铺,尽可能获得最大的客流量。下面的地图标注出该地区的三个人口中心:人口中心1坐标(-1,3),约有6万人,人口中心2坐标(1,3),约有2万人,人口中心3坐标(0,-4),约有3万人。
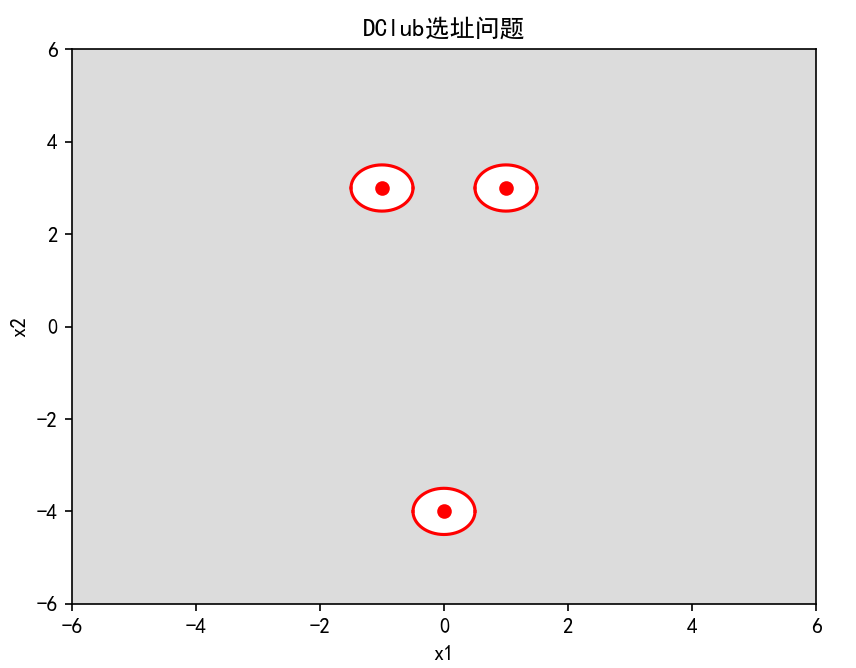
新店铺可以建在距离人口中心0.5英里以外的任何地方,也就是图中阴影部分。很显然,该模型决策变量只有两个:

根据以往经验,店铺从各人口中心获得的客流量服从“重力”模式——客流量与人口中心人口(千人)成正比,与1+距离平方成反比。由此我们得到目标函数:
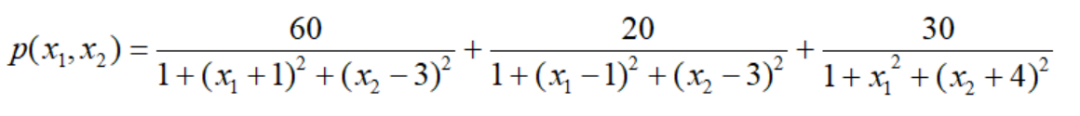
再根据约束条件,我们得到优化模型:
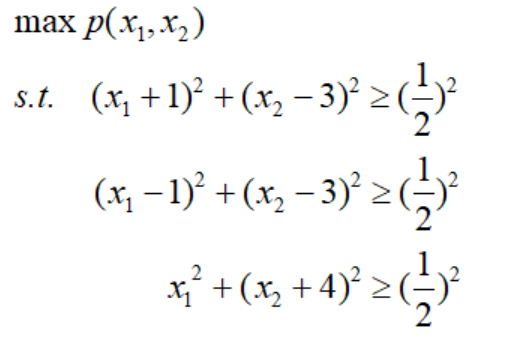
根据模型分类,可知DClub选址问题是非线性规划模型。利用三维图我们很容易画出目标函数的图像:
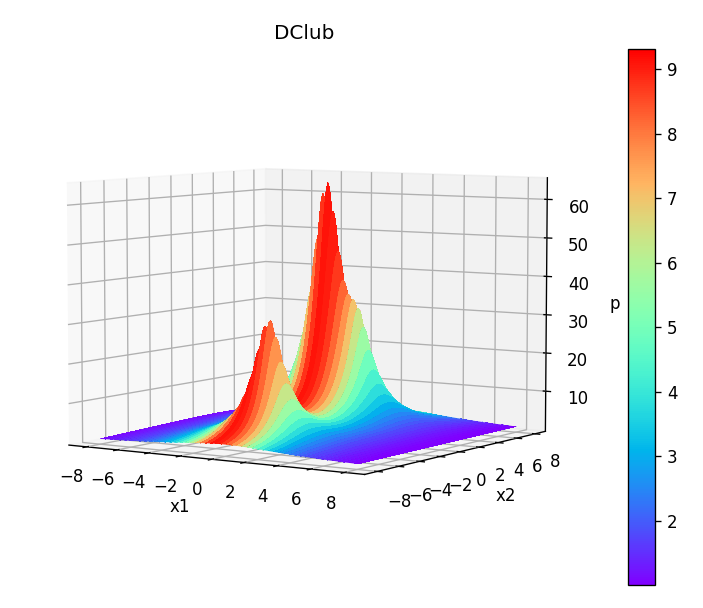
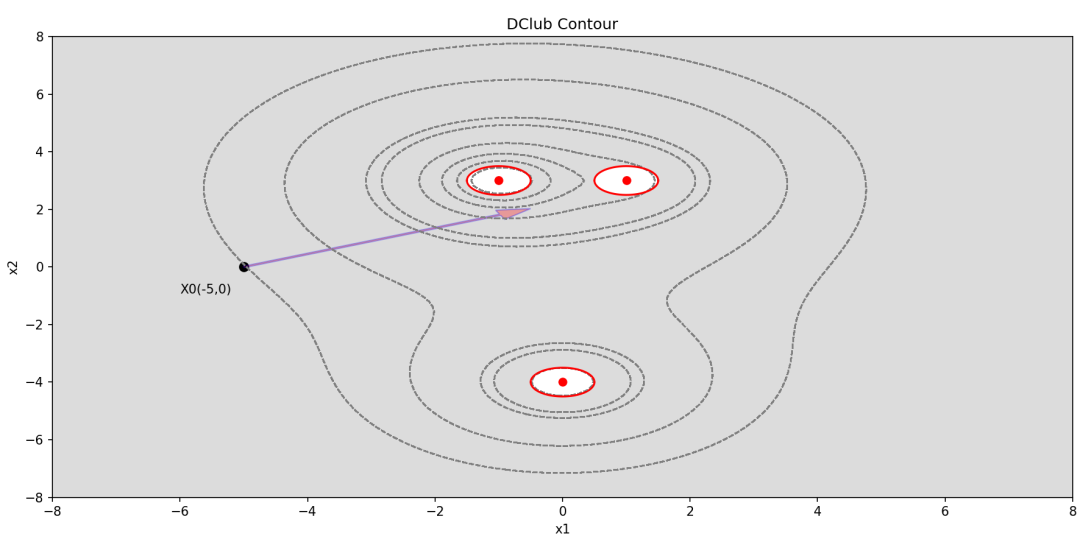
下面我们利用等高线来具体看一下搜索算法的原理:假设从点X0开始,经过四次,我们得到了模型的近似最优点X4,该过程为:

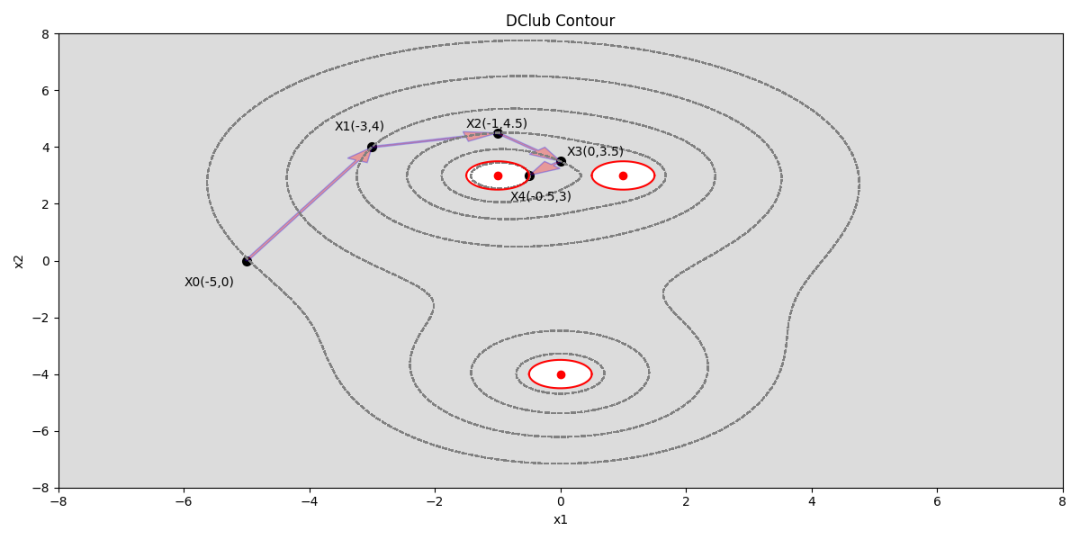
像这种便于绘图的优化模型,很容易找到最优解。如果对于更加复杂的优化模型,没办法通过绘图观察,就需要寻找一种特定的搜索算法才能找到最优解。我们知道,上述每一步迭代过程,都是在当前可行解的领域内寻找下一组对目标有改进的解,直到可行解领域内找不到更好的解。因此,我们定义:
局部最优解(local optimum)
倘若一组可行解周围足够小的邻域内不存在优于该解的可行点,则称该解为局部最优解

从一个初始值开始,进行搜索算法迭代,到达局部最优后,算法停止迭代。
进一步,我们可以定义全局最优解(global optimum):
如果全局范围内不存在目标值优于某可行解的其他可行点,则称该可行解为全局最优解

简单来说,全局最优解就是所有局部最优解中最优的那一组,因此有下面的结论:全局最优也是局部最优,局部最优不一定是全局最优.
比如DClub的例子,下面也是一个局部最优搜索的路径:
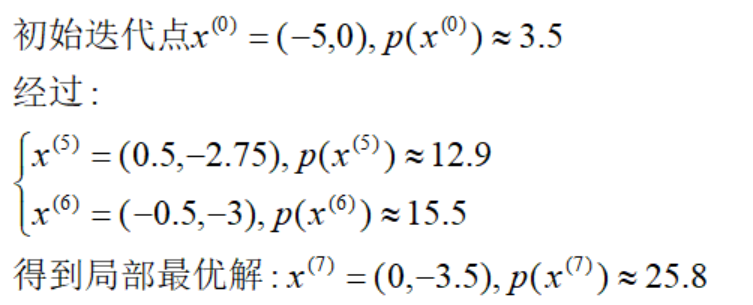
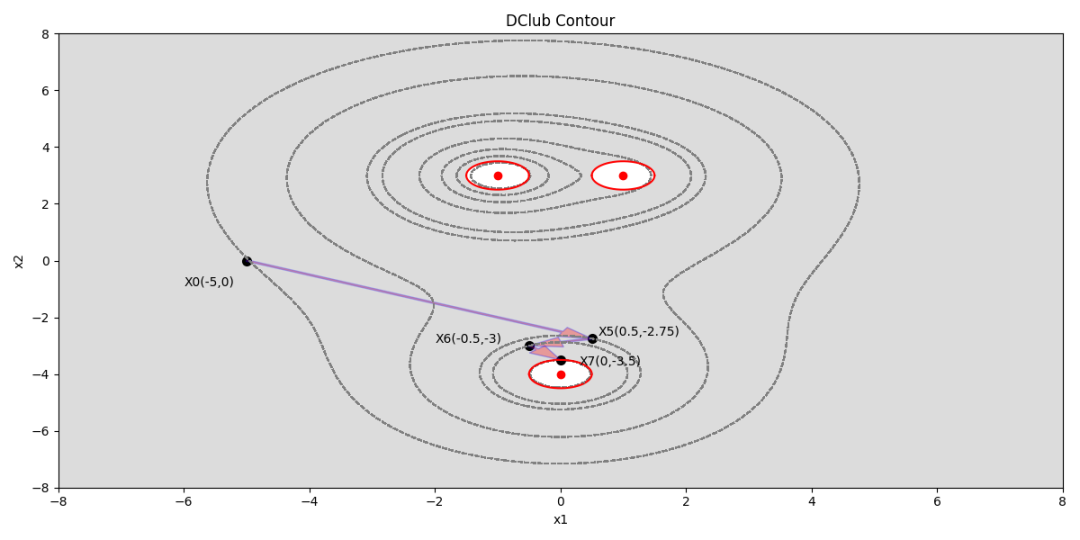
两条搜索路径:X0→X1→X2→X3→X4;X0→X5→X6→X7,都到达了局部最优解,但明显X4的目标值优于x7,所以X7不是全局最优.
接下来的一个问题自然是——如何找到全局最优呢。最常用的方法是尝试不同的搜索算法(一般使用不同的初始点),选取其中最好的结果作为一种近似或启发式最优。这一点我们后面再说。现在我们先来关注另外一个问题。
2
可行改进方向
上一节展示了搜索算法的基本逻辑,但是并没有给出改进目标值的搜索过程方法。先定义:

根据定义,模型在当前解可以往任意一个方向进行迭代得到下一个解,但为了能保证目标值的提高,我们要限制其在改进方向上进行迭代,因此再定义:

顾名思义,改进方向不考虑约束条件,只要保证下一次迭代的目标值优于当前的目标值即可;而可行方向要在可行域范围内考虑,但不保证下一次的目标值优于当前目标值,还要有可行性。注意这里的λ取值——足够小,意味这是在当前解的领域内进行搜索下一个可行解。
举个例子,双原油模型的表达式为:
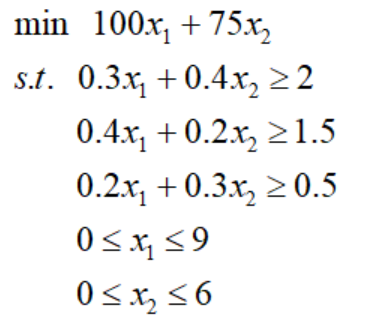
将其约束条件可视化,其中灰色部分为可行域:
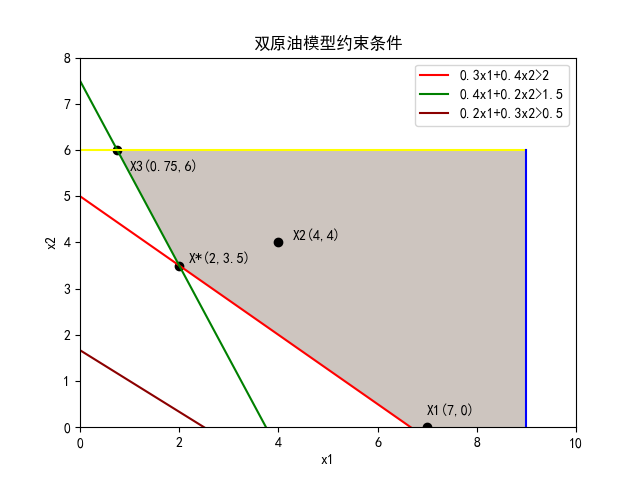
显然,图中x2往任意方向前进一小段都不违反约束条件,因此对于x2每一个Δx都是可行方向,但并非每一个可行方向都是改进方向,比如Δx=(0,-1);对于x1,沿Δx=(0,1)是可行方向,Δx=(0,-1)违反约束条件;对于x3,沿Δx=(0,1)方向违反约束条件,因此不是可行方向,但是改进方向。
模型优化的方向自然是——可行改进方向。也就是,当前解往可行的改进方向走一段微小距离,下一个点必定是在可行域内,且目标值是改进的。这里自然引发一个问题,沿着可行改进方向的步长是微小的,那么这个步长最多能多长仍能保证可行且目标值是改进的呢?我们定义最佳步长λ:
搜索算法通常沿着可行改进方向最大程度改进目标值,并保持可行的距离作为最佳步长

这里从两个方面理解:最大程度改进目标值的距离以及保持可行的最大的距离;当目标值停止或者约束条件不满足时,固定λ值,并选取一个新的改进方向。
举个例子,考虑数学模型的最佳步长:

最佳步长方法有了,就剩下最后一个问题——如何确定改进方向。改进方向是相对目标值来说的。如果目标函数f可微,根据微分定义,搜索算法在当前解x往方向Δx前进步长λ后目标函数的变化值可近似为:

根据此,梯度信息为搜索方向是否改进提供了一个代数检验方法:

进一步,因为实数的平方都大于等于0,数学上我们知道,梯度是函数值变化最快的方向。只要方向Δx对准梯度方向(或反方向),就可以使得目标值沿着改进方向进行迭代:

举个例子加以说明。

这里有一点需要说明,梯度方向是一个改进的方向,但不总是最佳的搜索方向。这一点以后会展开说明。
3
3A算法
根据前面的铺垫,我们可以给出第一套搜索算法——3A算法。

沿用上面DClub搜索的例子来说明3A算法。
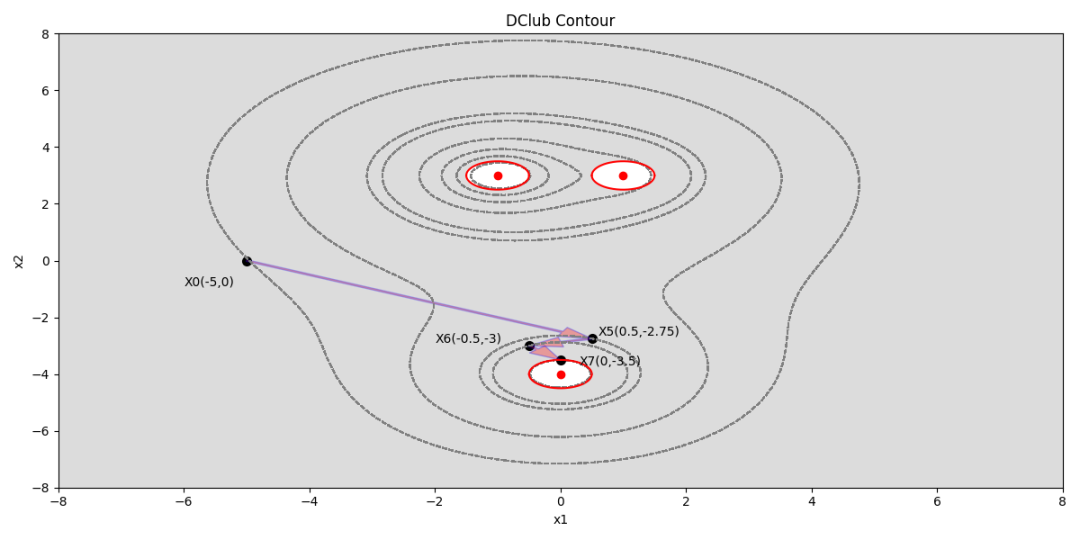
模型初始可行解X0=(-5,0),令t=0,很显然X0存在可行改进方向,跳过算法第1步,构建可行改进方向,选择的方向是Δx=(2,-1),这里根据作图法确定最佳步长λ=2.75,得到第一个迭代点:
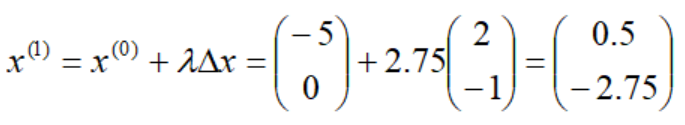
令t=t+1=1,返回第1步。选择可行改进方向Δx=(-4,-1),确定最佳步长λ=0.25,得到第二个迭代点:
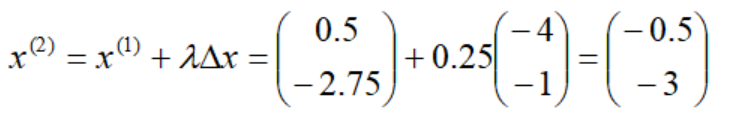
令t=t+1=2,返回第1步。选择可行改进方向Δx=(1-1),确定最佳步长λ=0.5,得到第三个迭代点:
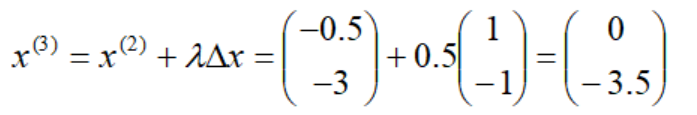
令t=t+1=3,返回第1步。不存在可行改进方向,停止搜索,得到局部最优点X3。
这里有四点内容需要注意。第一,这里的改进方向不是梯度方向,而是随机选取一个改进方向,说明3A算法的搜索方向不一定是往函数值下降最快的方向迭代;第二,确定最佳步长根据作图法,也就是说,这里使用约束条件来得到最佳步长是不行的,这与前面的例子有所不同,这是因为这两者的目标函数表达式不是同类型的。
假如在初始可行解X0沿着梯度方向改进,并且只利用约束条件寻找最佳步长,那么程序将是这样,计算函数在点X0的梯度约为(1,0.45);按照约束条件计算出来的步长取值范围为:
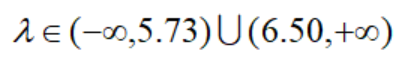
显然,最佳步长λ无法根据约束条件来确定,我们作图就能一目了然:在X0往梯度方向改进,步长不能太小也不宜过大,否则都是负优化,根据作图可以确定最佳步长约为4.7
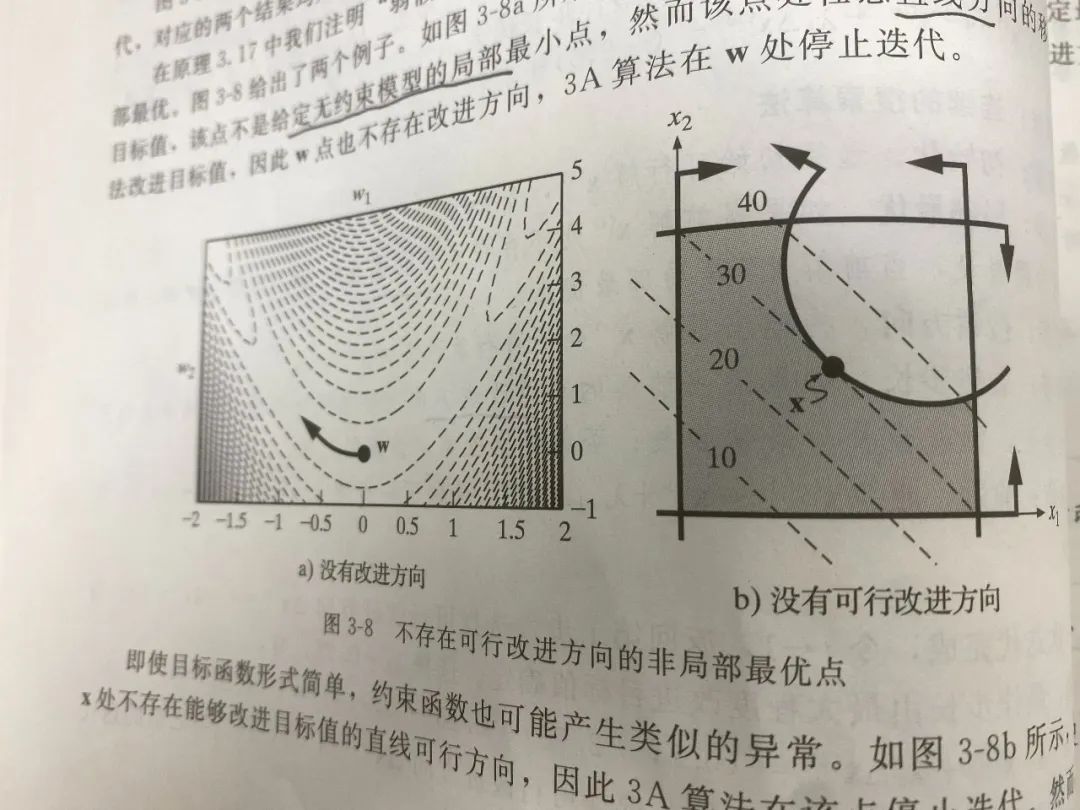
第三,3A算法强调了当不存在可行改进方向时,模型是在弱假设的前提下局部最优。这里的弱假设的意思是说——存在没有可行改进的方向的当前解不是局部最优。
比如下面两个例子:图a沿着w曲线方向可改进目标,但任意直线方向都无法改进目标值,即没有改进方向;图b在x处没有可行改进方向,但显然存在与x相邻的改进方向,即没有可行改进方向。
第四,3A算法提到了模型无界的情况。所谓的无界是指——如果沿某一可行改进方向前进任意步长都能同时改进目标值并保持可行性,则该模型无界(unbounded)。
举个最简单的例子加以理解。

4
保证局部最优即全局最优的条件
第一节我们就知道,局部最优不一定是全局最优。那么有没有一种满足某种条件下,局部最优就是全局最优呢。答案是有的——凸集与线性目标的全局最优性:

对于一个具有线性目标和凸可行集的优化模型,若3A算法在一个可行解处停止且不存在可行改进方向,则该可行解是全局最优解。换句话说,对于具有线性目标和凸集的模型,局部最优解就是全局最优解。
这里有两个名词需要解释,线性目标和凸可行集。
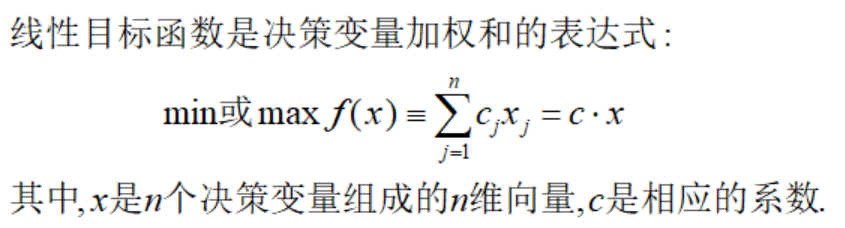
显然,目标函数f的梯度为常数,恒等于向量c,根据搜索方向改进的代数检验方法,对于最大化目标函数,当且仅当cΔx>0,方向Δx是改进方向;对于最小化目标函数,当且仅当cΔx<0,方向Δx是改进方向.
接下来只需要保证下一次迭代的地方是可行的即可——凸可行集:
如果可行域内任意两点的连线都在可行域内,则称该可行域为凸集

两点的连线中的任意一点可表示为:
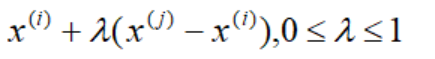
也就是说,若优化模型的可行集是凸集,那么对任意可行解始终存在指向另一个解的可行方向.
据此,我们可以证明凸集与线性目标的全局最优性:

最后,介绍紧约束的概念结束今天的内容。紧约束(tight constraint),又称积极约束(active constraint)或起作用约束(binding constraint),它表示在当前解x处恰好满足等式的约束.
仍以双原油为例,点X1=(7,0)满足不等式约束:
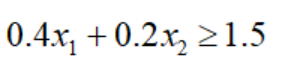
该约束是不起作用的,因为0.4*7+0.2*0=2.8>1.5。但该约束在点X*=(2,3.5)是起作用的:0.4*2+0.2*3.5=1.5
附赠作图的代码(部分):
import numpy as np
from matplotlib import cm
import matplotlib.pyplot as plt
plt.rcParams['figure.dpi'] = 100 #设置图片分辨率
class Plot(object):
def __init__(self,x,y,z):
'''
初始化对象
:param x: x轴数据集
:param y: y轴数据集t
:param z: z轴数据集
'''
self.x = x
self.y = y
self.z = z
def plot_3d(self):
'''
作3D图像
:return:
'''
fig = plt.figure(figsize=(12,6))
ax = plt.axes(projection='3d')
# ax.plot3D(x1, x2, p, 'gray')
surf = ax.plot_surface(self.x,self.y,self.z,cmap=cm.rainbow)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('p')
ax.set_title('DClub')
fig.colorbar(surf)
plt.show()
def plot_circle(self,center=(3, 3),r=2):
'''
作圆
:param center: 圆点坐标
:param r: 半径
:return:
'''
x = np.linspace(center[0] - r, center[0] + r, 5000)
y1 = np.sqrt(r**2 - (x-center[0])**2) + center[1]
y2 = -np.sqrt(r**2 - (x-center[0])**2) + center[1]
plt.plot(x, y1, c='r')
plt.plot(x, y2, c='r')
plt.fill_between(x, y1, y2, facecolor="white")
def plot_contour(self):
'''
等高线绘制,并且制作算法迭代路径,可自行定义
:return:
'''
plt.rcParams['axes.facecolor'] = '#DCDCDC'
plt.figure(figsize=(12,6))
CS = plt.contour(x1,x2,p,levels=[3.5,6,11.5,21.6,36.1,54],linestyles=6*['--'],colors=6*['gray'],linewidths=[1])
self.plot_circle((-1,3),0.5)
self.plot_circle((1,3),0.5)
self.plot_circle((0,-4),0.5)
plt.scatter([-1, 1, 0], [3, 3, -4], color='r')
# plt.grid(True)
plt.clabel(CS, inline=0, fontsize=0)
plt.scatter([-5,-3,-1,0,-0.5],[0,4,4.5,3.5,3],color='black',linewidths=2)
plt.text(-6,-1,s='X0(-5,0)',verticalalignment='bottom')
plt.text(-3.6,4.5,s='X1(-3,4)',verticalalignment='bottom')
plt.text(-1.5,4.6,s='X2(-1,4.5)',verticalalignment='bottom')
plt.text(0.1,3.6,s='X3(0,3.5)',verticalalignment='bottom')
plt.text(-0.8,2,s='X4(-0.5,3)',verticalalignment='bottom')
plt.arrow(-5, 0, 2, 4, length_includes_head=True, head_width=0.35, width=0.05,alpha=0.3, fc='red', ec='blue')
plt.arrow(-3, 4, 2, 0.5, length_includes_head=True, head_width=0.35, width=0.05,alpha=0.3, fc='red', ec='blue')
plt.arrow(-1, 4.5, 1, -1, length_includes_head=True, head_width=0.35, width=0.05,alpha=0.3, fc='red', ec='blue')
plt.arrow(0, 3.5, -0.5, -0.5, length_includes_head=True, head_width=0.35, width=0.05,alpha=0.3, fc='red', ec='blue')
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("DClub Contour")
plt.tight_layout()
plt.show()
if __name__ == '__main__':
n = 100
a = np.linspace(-8, 8, 100)
x1 = np.repeat(a, n, axis=0)
x2 = np.tile(a, n)
x1, x2 = np.meshgrid(x1, x2)
p = 60 / (1 + (x1 + 1) ** 2 + (x2 - 3) ** 2) + 20 / (1 + (x1 - 1) ** 2 + (x2 - 3) ** 2) + 30 / (
1 + x1 ** 2 + (x2 + 4) ** 2)
P = Plot(x1,x2,p)
P.plot_3d()
P.plot_contour()import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
x = np.linspace(0,9,500)
y1 = -3/4*x+5
y2 = -2*x+7.5
y3 = -2/3*x+5/3
y = np.piecewise(x,[x<2,x>=2],[lambda x:-2*x+7.5,lambda x:-0.75*x+5]) #分段函数
plt.plot(x, y1, c='r',label='0.3x1+0.4x2>2')
plt.plot(x, y2, c='g',label='0.4x1+0.2x2>1.5')
plt.plot(x, y3, c='#8B0000',label='0.2x1+0.3x2>0.5')
plt.plot(x, np.tile(np.array(6), 500), c='#FFFF00')
plt.plot(np.tile(np.array(9), 500),np.linspace(0,6,500), c='b')
plt.fill_between(x, y, np.tile(np.array(6), 500), where=(x>=0.75)&(x<=9),facecolor="#CDC5BF")
plt.scatter([7,4,0.75,2],[0,4,6,3.5],color='black')
plt.xlim(0,10)
plt.ylim(0,8)
plt.text(7,0.2,s='X1(7,0)',verticalalignment='bottom')
plt.text(4.3,4,s='X2(4,4)',verticalalignment='bottom')
plt.text(1,5.5,s='X3(0.75,6)',verticalalignment='bottom')
plt.text(2.2,3.5,s='X*(2,3.5)',verticalalignment='bottom')
plt.legend()
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("双原油模型约束条件")
plt.show()求解偏导数与不等式组代码:
import os
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
import tensorflow as tf
x1 = tf.Variable(-5.0)
x2 = tf.Variable(0.0)
with tf.GradientTape(persistent=True) as t:
p = 60 / (1 + (x1 + 1) ** 2 + (x2 - 3) ** 2) + 20 / (1 + (x1 - 1) ** 2 + (x2 - 3) ** 2) + 30 / (1 + x1 ** 2 + (x2 + 4) ** 2)
x1_grad, x2_grad= t.gradient(p, [x1,x2])
print(x1_grad.numpy(),x2_grad.numpy())
from sympy import symbols, solve
lam = symbols('lam')
x1 = -5+lam
x2 = 0.45*lam
f1 = (x1 + 1) ** 2 + (x2 - 3) ** 2 - 0.25
f2 = (x1 - 1) ** 2 + (x2 - 3) ** 2 - 0.25
f3 = x1**2 + (x2 + 4) ** 2 - 0.25
solve([f1 >=0, f2 >= 0, f3 >= 0])