一、e的值
自然常数(也称欧拉数)e是数学中最重要的数字之一。
2.7182818284590452353602874713527......
二、从复利理解e
设想你在一家银行有一个银行账户,该银行付给你一个慷慨的利息年利率12%,一年计一次复利.你将一笔初始存款存入账户.每一年你的财富增加12%.这意味着,n年后,你的财富会增加到原来的倍.特别地,一年后,你的财富就是(1+0.12)乘以原始存款.如果你最开始存入了100x元,年底你会得到112元。
在相同的年利率下,复利计算得越频繁,结果就会越好。
年利率依旧为12%、每年计三次复利,并将它除以3会得到4%,然后计算复利三次,我们的财富将会增加到原来的倍,其结果是1.124864.这还是高了些.要是每年计四次呢?那将是
倍,结果近似为1.1255,这就更高了。
那么现在的问题是,它会又尽头么?如果你以相同的年利率计算复利越来越频繁,一年后你会得到大把大把的现金,还是这一切有某种上限?
为了回答这个问题,让我们来求助于一些符号.首先,假设以年利率12%每年计n次复利.这意味着,每次计算复利时,复利的利率是0.12/n。
1、在一年中计算n次后,我们的原始财富增长的倍数为 。
。
2、如果复利计算得越来越频繁时会怎样;这意味着n变得越来越大.也就是说,我们想知道,当n→∞时上式的极限 
3、我们也很想知道,当利率不是12%时会发生什么.因此,用r代替0.12,并关心更一般的极限。
4、首先,设h=r/n,这样n=r/h.那么当n→∞时,我们看到h→0+(因为r是常数),故
5、完整计算

6、于是我们知道

令r=1

三、e的曲线
的值随着 n 变得越来越大而接近 e:

有时e也可以使用阶乘表示
四、现实生活中的例子
每当系统呈指数级和连续增长时,e 就会出现:人口、放射性衰变、利息计算等等。

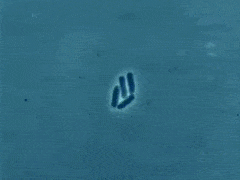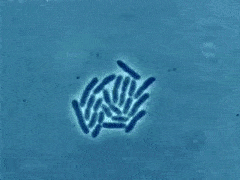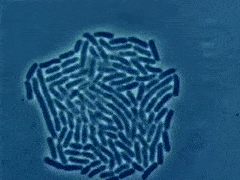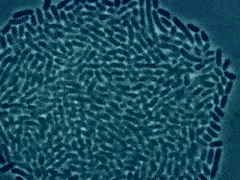
面包长时间放在外面时,面包会发生变色,这通常被称为面包霉菌。这种面包霉菌是一种微生物,当面包保持在正常室温下时会生长。面包霉菌以惊人的速度生长。这种快速增长被定义为“指数增长”。

在医院的病理学测试中,病理学家遵循指数增长的概念来培养从样本中提取的微生物。当微生物获得无限的资源和合适的环境时,它们会以快速的速度生长。