什么是傅里叶变换?
对随时间变化的曲线,不再从时间轴上去看他的变化,而是消去时间因子,从出现的频率上来分析他的变化情况。
例如:
股市变化曲线是随时间变化的曲线,而通过傅里叶变化,将不再是时间频域上分析,而是频率频域上分析,与时间没有关系了。(最简单的就是对sin或者cos进行变换来看。)
对于光场传输的话,光场在传输方向上的空间分布(类似时间),通过傅里叶变换,将无空间特性,而是频率特性。
在时间域(或者空间域)是一段变化的波,而对应的频率域可能就是一个简单的脉冲点或者线。
如一段音乐


一小段波的变化可能对应一个音符,也就是时域与频域的对应。
不同频率波的叠加


黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。
时域的基本单元就是“1秒”,如果我们将一个角频率为正弦波cos(w0t)看作基础,那么频域的基本单元就是w0。
近似矩形波在频域里的另一个模样:
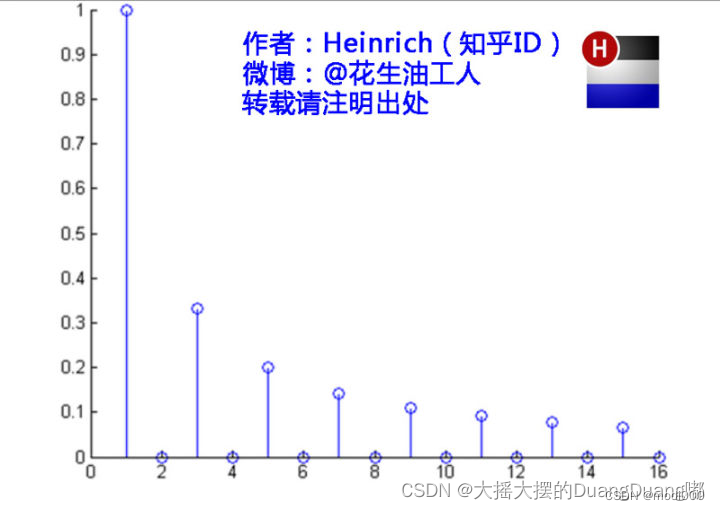


注:傅里叶变换,是将时间域的合成波形,分解成无数个周期恒定的子波,而子波的振幅高度就是频域高度,不同频率值即为不同的子波。
我们眼中的世界就像皮影戏的大幕布,幕布的后面有无数的齿轮,大齿轮带动小齿轮,小齿轮再带动更小的。在最外面的小齿轮上有一个小人——那就是我们自己。我们只看到这个小人毫无规律的在幕布前表演,却无法预测他下一步会去哪。而幕布后面的齿轮却永远一直那样不停的旋转,永不停歇。这样说来有些宿命论的感觉。
傅里叶变换有什么用?
可以用来处理 时间域(空间域)中难以实现的情况,而通过频率域则很简单。
比如,对于sin(3x)+sin(5x)的图形,需要去除sin(5x)函数,在空间域实现起来很难,但是在频率则很简单。
怎么来做呢?通过前一章的侧面观察法,我们可以发现,只需要在频率域去除这一频率脉冲就可以了,然后,需要的话,通过一个反傅里叶变换,不就实现了吗?是不是,这样对于复杂的情况就简单多了!
尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
这里再补充一个 相位谱
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。

也就是说,相位谱的大小,是距离频率轴最近的波峰往下投影,然后该投影点到频率轴的距离,就是相位谱!


傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波。
再补充一个 虚数符号与欧拉公式
我们先来看看这个虚数符号 i ,它有什么样的意义呢?可能自从我们认识它后,只初步了解他的数学运算,其实它还有一定的物理意义:

这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
我们知道乘-1其实就是乘了两次 i使线段旋转了180度,那么乘一次 i 呢——答案很简单——旋转了90度。

引:傅里叶变换的意义与理解(详解)
————————————————
版权声明:本文为CSDN博主「大摇大摆的DuangDuang嘟」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/VJCP_90909Bu0/article/details/127315765