文章目录
Part.I Introduction

因为在学习模糊度固定的时候涉及了『搜索椭球』这一概念,很想知道是如何用椭球来表示搜索空间的。出于好奇,在查阅了一些相关文献,终于解决了笔者的疑惑,此篇博文就简要记录一下如何根据协方差矩阵来绘制椭球。
下面是得到的一些结论:
- 对协方差矩阵进行奇异值分解得到奇异值和奇异向量
- 协方差矩阵的奇异值表征椭球的向径长度
- 协方差矩阵的奇异向量表征椭球的向径指向
Part.II 二维情况
Chap.I 绘图函数
%% 根据 奇异值分解绘制相关椭圆
function draw_oval1(cova)
[U,S,V] = svd(cova); % 奇异值分解
% [U,S] = eig(cova); % 特征值
angle = cart2pol(U(1, :), U(2, :))*180/pi;
beta = angle(1, 1);
if beta<0; beta=beta+180; end
semimajor = sqrt(S(1, 1)); % 长轴长度(一半)
semiminor = sqrt(S(2, 2)); % 短轴长度(一半)
alpha = linspace(0, 360, 2000)';
level = 1;
% 椭圆坐标点
ellipse_X = 0+sqrt(level)*(semimajor*cosd(alpha)*cosd(beta)-...
semiminor*sind(alpha)*sind(beta));
ellipse_Y = 0+sqrt(level)*(semimajor*cosd(alpha)*sind(beta)+...
semiminor*sind(alpha)*cosd(beta));
%% 可视化
% figure
hold on
box on
grid on
set(gca, 'linewidth', 1.5)
% 置信椭圆
plot(ellipse_X, ellipse_Y, 'Color', [0, 102, 255]/255,...
'LineStyle', '-', 'LineWidth', 3),
level = 1.5;
quiver(0,0,U(1,1)*semimajor*level,U(1,2)*semimajor*level,'LineWidth',2.0);
quiver(0,0,U(2,1)*semiminor*level,U(2,2)*semiminor*level,'LineWidth',2.0);
str=sprintf('a=%.2f\nb=%.2f\n',semimajor,semiminor); % len=%d\n
str=[str,sprintf('e=%.2f\nang=%.2f',(semimajor-semiminor)/semimajor,beta)];
text(2, -3, str, 'FontSize', 16, 'FontWeight', 'bold')
axis equal
end
Chap.II 调用示例与结果
调用示例:
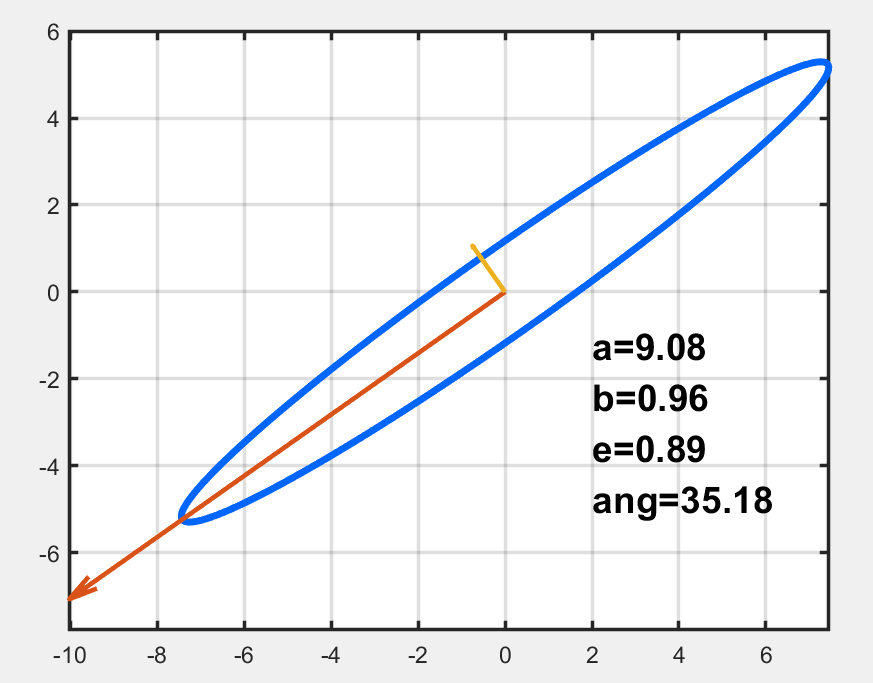
Z=[55.4 38.4;38.4 28];
draw_oval1(Z)
结果:
Part.III 三维情况
Chap.I 绘图函数
%% 根据 奇异值绘制相关椭球
function draw_ellipsoid(A)
[theta,phi] = meshgrid(0:10:360,-90:10:90);
[nr,nc] = size(theta);
Theta = reshape(theta,nr*nc,1)*pi/180;
Phi = reshape(phi,nr*nc,1)*pi/180;
%[R,V] = eig(A);
[R,V,U] = svd(A); % 奇异值分解, sqrt(V) 是半长轴, R 是向量方向
V=sqrt(V);
nd = size(A,1);
V = abs(V);
xyz = V(1,1)*sin(Phi)*R(:,1)'+ V(2,2)*cos(Phi).*cos(Theta)*R(:,2)'+ V(3,3)*cos(Phi).*sin(Theta)*R(:,3)';
P1 = reshape(xyz(:,1),nr,nc);
P2 = reshape(xyz(:,2),nr,nc);
P3 = reshape(xyz(:,3),nr,nc);
plot3(0,0,0);
hold on; surfl(P1, P2, P3);
%绘制向量箭头
level=1.5;
quiver3(0,0,0,R(1,1)*V(1,1)*level,R(2,1)*V(1,1)*level,R(3,1)*V(1,1)*level,'LineWidth',2.0);
quiver3(0,0,0,R(1,2)*V(2,2)*level,R(2,2)*V(2,2)*level,R(3,2)*V(2,2)*level,'LineWidth',2.0);
quiver3(0,0,0,R(1,3)*V(3,3)*level,R(2,3)*V(3,3)*level,R(3,3)*V(3,3)*level,'LineWidth',2.0);
end
Chap.II 调用示例与结果
调用示例:
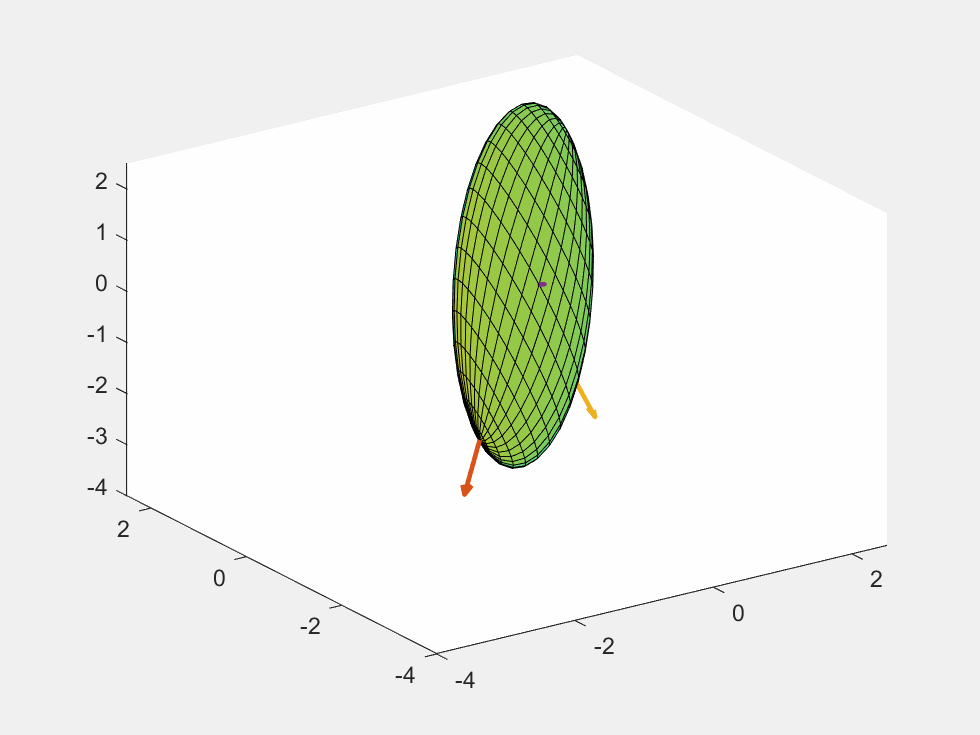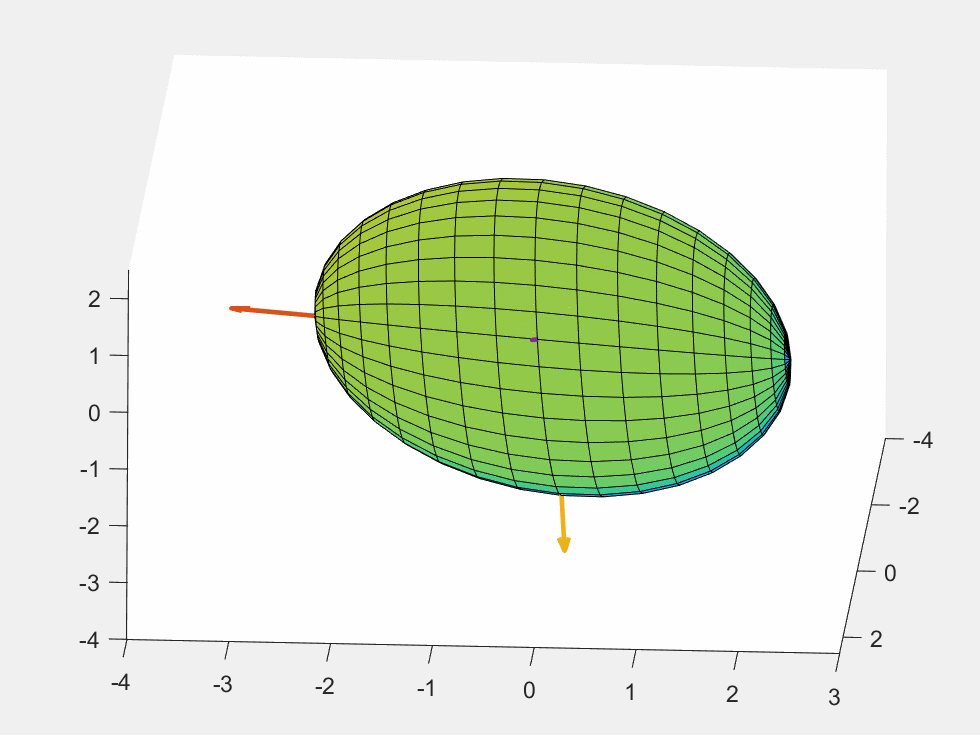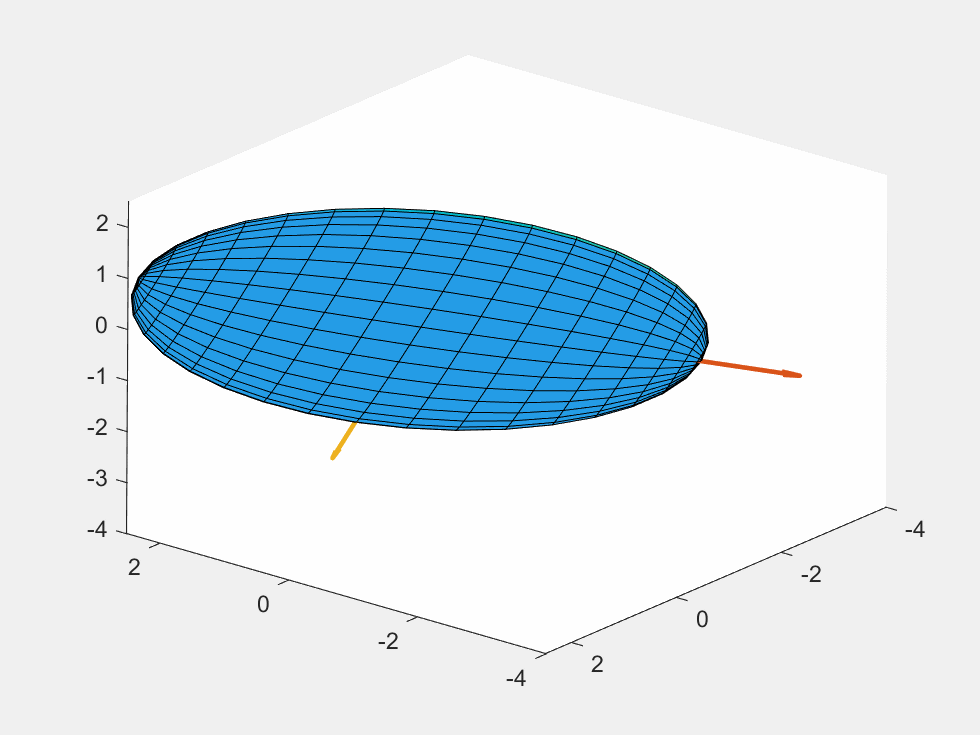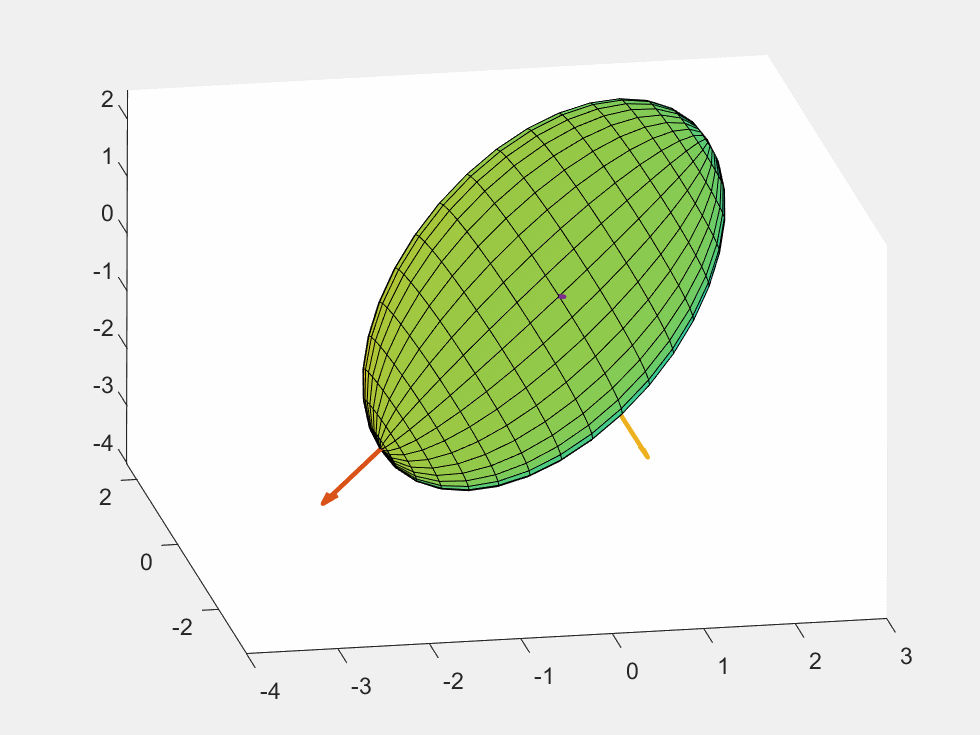
cova=[6.290 5.978 0.544;5.978 6.292 2.340;0.544 2.340 6.288];
draw_ellipsoid1(cova)
saveGIF()
结果:
Chap.III 补充函数
可以看到,笔者将绘制结果保存成了一个gif,所用到的函数为:
%% generate GIF and save file.
function saveGIF()
sdir='C:\Users\OHanlon\Desktop\temp\ellipsoid.gif';
%surf(peaks,'EdgeColor','yellow')
img_num = 120;
for i=1:img_num
camorbit(360/img_num,0,'data',[0,0,1]) %[0 0 1]表示按z轴旋转。
M=getframe(gcf);
nn=frame2im(M);
[nn,cm]=rgb2ind(nn,256);
if i==1
imwrite(nn,cm,sdir,'gif','LoopCount',inf,'DelayTime',0.1);%说明loopcount只是在i==1的时候才有用
else
imwrite(nn,cm,sdir,'gif','WriteMode','append','DelayTime',0.1)%当i>=2的时候loopcount不起作用
end
end
end
Part.IV 探究过程与存在的问题
Chap.I 探究过程
刚开始的时候,绕了一个弯路:因为之前有写过置信椭圆(误差椭圆)详解,里面可以用主成分分析来绘制样本的置信区域(椭圆);因为我不知道是如何来得到椭圆的长短半轴以及方向的,只是将里面用的函数当作一个黑盒子,只要我有样本数据,输进去它就会给我吐出来一个椭圆。所以我就用待画的椭圆来模拟一些样本数据,丢给那个函数就行了。但是这样存在一个问题:模拟出来的数据总是会存在离群值,从而导致绘制出来的椭圆并不是所给协方差,而是和它有一个微小的偏差(可以忽略不记)。
利用这种思路写的绘制函数如下:
function draw_oval(cova)
% ----------- 模拟数据 ---------------
len=300*10;
data=randn(len, 2);
data1=[];
while size(data1,1)~=size(data,1)
data1=data;
data=rmoutliers(data1,'mean');
end
R = chol(cova); % 上三角矩阵
data=data*R;
center = mean(data);
[coeff, ~, latent, ~, ~] = pca(data);
% r1 r2 为自定义的向量大小参数(模)
r1 = 6;
r2 = 3;
% p1 p2 为第一主轴和第二主轴上的点
p1 = r1*coeff(:, 1)'+center;
p2 = r2*coeff(:, 2)'+center;
% 主轴方向与X轴之间的夹角
angle = cart2pol(coeff(1, :), coeff(2, :))*180/pi;
% disp("第一主轴方向与 X 轴之间的夹角");
beta = angle(1, 1);
% 置信椭圆坐标(以 95% 为例)
semimajor = sqrt(latent(1, 1)); % 长轴长度(一半)
semiminor = sqrt(latent(2, 1)); % 短轴长度(一半)
alpha = linspace(0, 360, 2000)';
% 卡方分布表
% https://people.richland.edu/james/lecture/m170/tbl-chi.html
% level = 4.605; % 90%
% level = 5.991; % 95%
% level = 9.210; % 99%
level = 10.597; % 99.5%
% 椭圆坐标点
ellipse_X = center(1, 1)+sqrt(level)*(semimajor*cosd(alpha)*cosd(beta)-...
semiminor*sind(alpha)*sind(beta));
ellipse_Y = center(1, 2)+sqrt(level)*(semimajor*cosd(alpha)*sind(beta)+...
semiminor*sind(alpha)*cosd(beta));
%% 可视化
% figure
hold on
box on
grid on
% 原始数据
% scatter(data(:, 1), data(:, 2), 15, 'LineWidth', 1.2,...
% 'MarkerEdgeColor', [151, 138, 189]/255,...
% 'MarkerFaceColor', [151, 138, 189]/255);
% t=10;
% xlim([-t, t]); % 在这里更改显示界限
% ylim([-t, t]);
set(gca, 'linewidth', 1.5)
% 置信椭圆
plot(ellipse_X, ellipse_Y, 'Color', [0, 102, 255]/255,...
'LineStyle', '-', 'LineWidth', 3),
% 第一主轴方向
arrow_1 = annotation('arrow', 'Color', [162, 20, 47]/255,...
'HeadStyle', 'cback2', 'LineWidth', 3, 'HeadWidth', 20, 'HeadLength', 20);
arrow_1.Parent = gca;
arrow_1.X = [center(1, 1), p1(1, 1)];
arrow_1.Y = [center(1, 2), p1(1, 2)];
% 第二主轴方向
arrow_2 = annotation('arrow', 'Color', [0, 114, 189]/255,...
'HeadStyle', 'cback2', 'LineWidth', 3, 'HeadWidth', 20, 'HeadLength', 20);
arrow_2.Parent = gca;
arrow_2.X = [center(1, 1), p2(1, 1)];
arrow_2.Y = [center(1, 2), p2(1, 2)];
% 中心点
plot(center(1, 1), center(1, 2),...
'Marker', 'o',...
'MarkerSize', 8,...
'MarkerEdgeColor', [162, 20, 47]/255,...
'MarkerFaceColor', [162, 20, 47]/255);
% title('主轴方向和置信椭圆', 'FontSize', 16, 'FontWeight', 'bold')
str=sprintf('a=%.2f\nb=%.2f\n',semimajor,semiminor); % len=%d\n
str=[str,sprintf('e=%.2f\nang=%.2f',(semimajor-semiminor)/semimajor,beta)];
text(2, -3, str, 'FontSize', 16, 'FontWeight', 'bold')
axis equal
end
后来对pca函数进行了一下研究,发现pca就是对样本的协方差矩阵做了一个奇异值分解,椭圆的长短半轴和方向都是根据分解结果得到的。蓦然回首,那人却在灯火阑珊处。所以上面的是直接用奇异值分解对协方差矩阵进行了分解,然后直接绘制椭圆的函数。
然后,在做三维椭球绘制的时候,我发现特征值和奇异值有着千丝万缕的联系,但是这种关系搞得我云里雾里,只知道求椭球参数用奇异值分解也行,用特征值和特征向量也行,只是特征向量和奇异向量貌似只有顺序不一样?
Chap.II 存在的问题
- 只会绘制二维和三维的情况,但是更高维度的呢?
- 有大佬总结用 R 语言进行相关系数的可视化[3],有点好看,用空学学。