蒙特卡洛树搜索（新手教程）

本篇博客为《Monte Carlo Tree Search – beginners guide》的翻译，水平有限，有兴趣的朋友可以直接阅读原文。

很长一段时间以来，学术界普遍认为，机器在围棋领域达到人类大师的专业等级是不现实的。这被视为AI的一个“圣杯”，至少是在未来十年中仍难以抵达的一个里程碑。20年多前，Deep Blue在国际象棋中击败了国际象棋世界冠军Garry Kasparov，成就了它的辉煌时刻。从那以后，没有出现和人类围棋大师水平相当的围棋引擎，于是有人主张围棋中存在“numerical chaos”，并且也在一些电影用被引用。
　　令人惊讶的是，Google DeepMind团队在2016年3月份发布的一个叫做Alpha Go算法，以4-1的成绩击败了韩国世界冠军李世石，这推翻了之前否定机器不可能战胜人类的科幻电影和怀疑论者。大约一年后，新发布的Alpha Zero以100-0的成绩战胜了它的前代Alpha Go，这是人类一个很难达到的高度。

Alpha Go/Zero是几种方法集成而成的一个工程杰作。Alpha Go/Zero的核心组件包括：

蒙特卡洛树搜索——使用PUCT函数的一种树遍历的特定变体
残差卷积神经网络——使用policy network（策略网络）和value network（价值网络）来进行比赛的评估和落子先验概率的估计
强化学习——通过自我对局来训练网络

本篇文章只关注蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）。

1. 简介

2006年，Remi Coulom开发了一款叫做Crazy Stone的围棋游戏，该款游戏表现令人惊讶，斩获了好几个锦标赛冠军。蒙特卡洛树就是该游戏的一个核心算法。
　　从全局来看，蒙特卡洛树搜索的主要目标是：给定一个游戏状态来选择最佳的下一步。本文的余下部分关注蒙特卡洛树的细节，并解释这个主要目标意味着什么。同时，我们将会不时回顾Alpha Go/Zero，并尝试解释DeepMind在Alpha Go/Zeros中使用了怎样的蒙特卡洛树搜索的变体。

双人有限零和顺序游戏

MCTS运行所在的框架/环境是一个游戏，它本身是一个非常抽象和宽泛的概念，因此这里我们只关注一种游戏类型：双人有限零和顺序游戏。这个名词一开始听起来会有些复杂，但是实际上非常简单，现在来让我们将它分解一下：

游戏：意味着我们在一种需要交互的情境中，交互通常会涉及一个或多个角色
有限：表明在任意时间点，角色之间存在的交互方式都是有限的
双人：游戏中只有两个角色
顺序：玩家依次交替进行他们的动作
零和：参与游戏的两方有完全相反的目标，换句话说就是，游戏的任意结束状态双方的收益之和等于零

我们可以很轻松的验证，围棋、国际象棋和井字棋都是双人有限零和顺序游戏：有两位玩家参与，玩家能进行的动作总是有限的，双方的游戏目标是完全相反的（所有游戏的结果之和等于0）。

如何表示一个游戏

形式上，游戏可以由一些基本数学实体表示。在一本博弈论的书中，你也许会找到如下定义： $定义：一个广义形式的游戏可以有一个元组定义：\\\Gamma_E=\{\mathcal{X,A},I,p,\alpha,\mathcal{H},H,\imath,\rho,u \}$ 这看起来会有些混乱，对于一个数学家来说深挖下去或许会非常有趣。
　　但如果从一个程序员的角度来看就有些使人困惑。幸运的是我们可以用一种常见的数据结构以来表示游戏——游戏树。
　　游戏树是一个数，其中每一个节点代表游戏的一个确定状态。从一个节点到该节点的一个子节点（如果存在）是一个移动。节点的子节点数目称为分支因子。游戏树的根节点代表游戏的初始状态。游戏树的终端节点是没有子节点的节点，至此游戏结束，无法再进行移动。终端节点的状态也就是游戏的结果（输/赢/平局）。
　　下面以井字棋游戏为例，形象地来看下什么是游戏树。

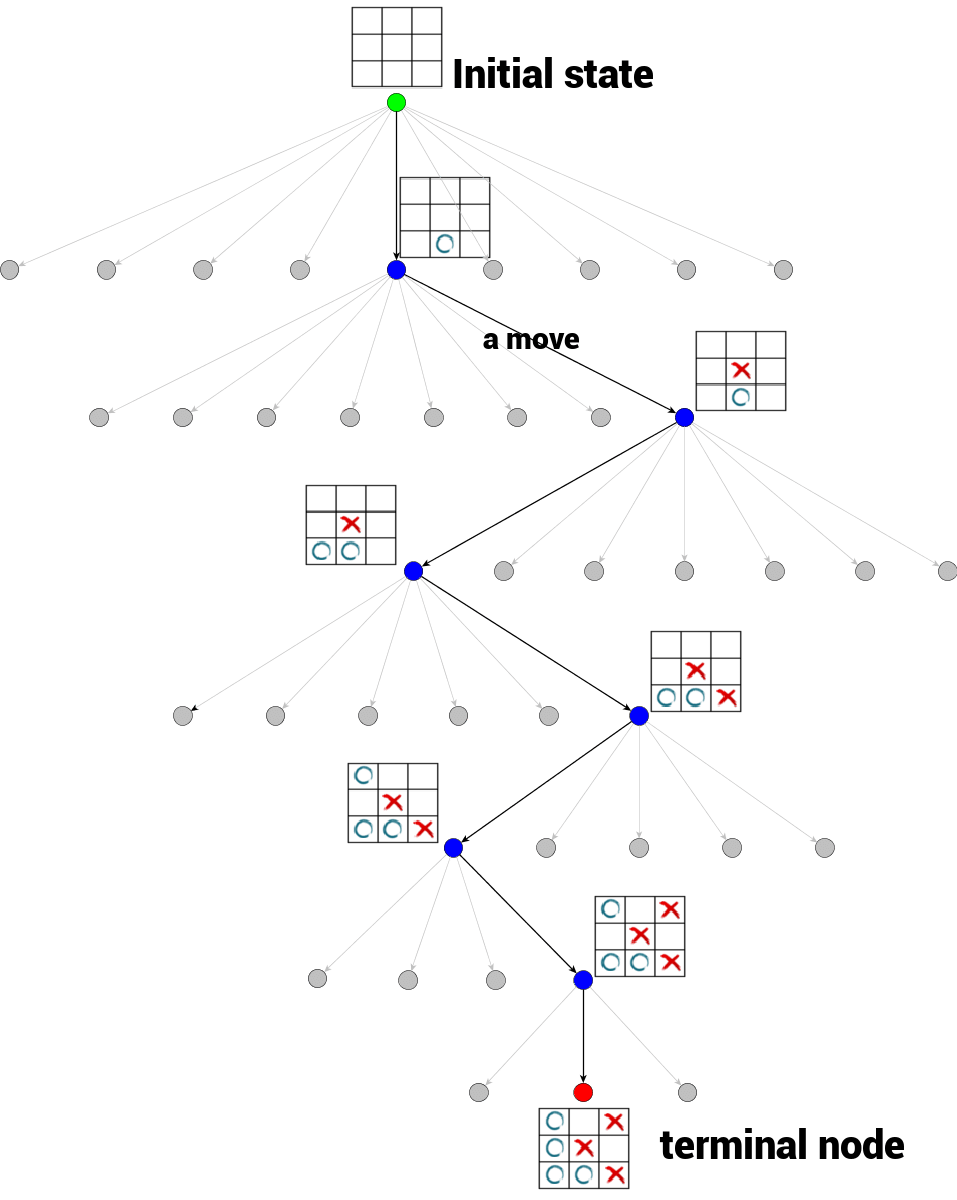
刚开局的时候，处于游戏树的根节点，代表井字棋游戏的初始状态，如上图所示，初始状态（绿点）是一张空棋盘。从一个节点到其任意一个子节点的过程称作一次移动（move）。分支因子每一步都不一样，这取决于树的深度，越到游戏后期可以落子的地方就越少，分支因子自然就越小。从树的根节点到终端节点的一次遍历代表一局游戏。
　　游戏树是一种递归的数据结构，每次选择完最佳的下一步时，会移动到下一个子节点，而这个子节点又是它子树的根节点。因此我们可以把一局游戏视为“最佳下一步”的一个问题序列，每一次都可以由一个不同根节点的游戏树表示。通常在实际应用中，我们不需要记住到当前状态的路径，因为这不是当前游戏状态的关注点。

什么是“最佳的下一步”？

重申一下，我们的终极目标是根据给定的游戏状态和游戏树找到“最佳下一步”。但这具体意味着什么呢？
　　关于这个问题并没有直接的答案。首先，我们根本无法提前知道对手的策略，对手可能是一个职业选手或者只是个并不怎么样的业余选手。以国际象棋为例，如果你的对手是一个业余选手，你也许可以选择简单的策略来欺骗他并迅速获得胜利。但是如果遇上很强的对手，仍然使用这个策略，情况可能就反过来了。
　　如果你完全不了解你的对手，这里有一个非常极端的策略，称为minmax。这个策略就是假设你的对手每一步都使用最优的策略，然后最大化你的游戏收益。在A和B之间的一个有限零和顺序游戏中（A最大化他的收益，而B希望最小化A的收益），minmax算法可以由下面的递推公式表示： $\begin{aligned} &v_A(s_i)=\max_{a_i}v_B(move(s_i,a_i)) v_A(\hat{s})=eval(\hat{s}) \\&v_B(s_i)=\min_{a_i}v_A(move(s_i,a_i)) v_B(\hat{s})=-eval(\hat{s})\end{aligned}\tag{1}$ 其中， $v_A$ 和 $v_B$ 是玩家A和B的效益函数， $m o v e$ 是给定当前状态 $s_i$ 和该状态下的动作 $a_i$ 产生下一个游戏状态的函数， $e v a l$ 是评估最终游戏状态的函数， $\hat{s}$ 是任意一个终端游戏状态。
　　简单来说，给定一个状态 $s$ ，你想要找到一个动作 $a_i$ 能够获得最大回报（假设你对手总是在最小化你的收益），这也是minmax算法的由来。我们所需要做的只是展开整个游戏树，并根据递归公式(1)来进行反向传播。
　　minmax最大的缺点是需要展开整个游戏树。对于有很大分支因子的游戏（比如围棋和国际象棋），这会导致游戏树非常巨大，并导致失败（搜索空间太大）。

有没有解决方法呢？

有，但是很少。一种方法是将游戏树扩展到一定的深度阈值 $d$ 。但是这样我们无法保证在深度 $d$ 处的任何节点都是终端节点。因此我们需要一个函数来评估非终端游戏状态。根据还未结束的棋局状态来预测输赢这对于人类来说非常容易。另一种克服游戏树规模过大的方法是通过 $\alpha-\beta$ 剪枝算法来对游戏树进行剪枝。 $\alpha-\beta$ 剪枝算法是一种加强的minmax，它以minmax的方式遍历游戏树，避免某些分支的展开。但这种方法的效果最好也只能和minmax一样，因为它是通过减小搜索空间来保证改进的。

2. 蒙特卡洛树搜索（MCTS）——基本概念

在蒙特卡洛树搜索算法中，最佳下一步的计算完全不同于上面提到的一游戏树。MCTS对游戏进行多次模拟，然后尝试基于模拟结果对最佳下一步进行预测。
　　MCTS的主要概念还是搜索。搜索是沿着游戏树的一组遍历的集合，单次遍历是从根节点（当前游戏状态）到一个未完全展开节点的路径。一个未完全展开的节点意味着它至少有一个未被访问的子节点。当遇到未完全展开的节点时，从该节点的子节点中选取一个未被访问过的用来进行一次模拟。模拟的结果然后反向转播是当前树的根节点，并更新节点的统计信息。当搜索结束时（受限于时间或计算能力），就可以根据收集的统计信息来决定下一步怎么走。
　　到目前为止，很多点可能还没有相互联系起来。接下来让我们根据上面的简单描述提出几个关键性的问题，并慢慢理解整个MCTS算法：

什么是未完全展开的游戏树节点？
搜索中“向下搜索”意味着什么？下一个节点如何选择？
什么是模拟？
什么是反向传播？
扩展的游戏树节点反向传播和更新哪些统计信息？
最终移动怎么选择？

模拟

首先让我们看看什么是模拟，这个概念不太依赖于其他术语的定义。模拟是一个移动的序列，从当前节点开始，到终端节点结束。也就是从当前游戏状态开始，一直玩玩玩（按照某种随机方式），玩到游戏分出胜负位置，从此当前到游戏结束每一步怎么下的序列。
　　那么，如何在模拟中如何选择移动呢？模拟中移动的选择是依据叫做rollout策略的函数： $s_i\rightarrow a_i$ 即根据当前游戏状态产生下一个移动。实际应用中，rollout策略往往会被设计成快速的，从而能够快速进行多次模拟，默认的rollout策略函数是均匀随机分布。

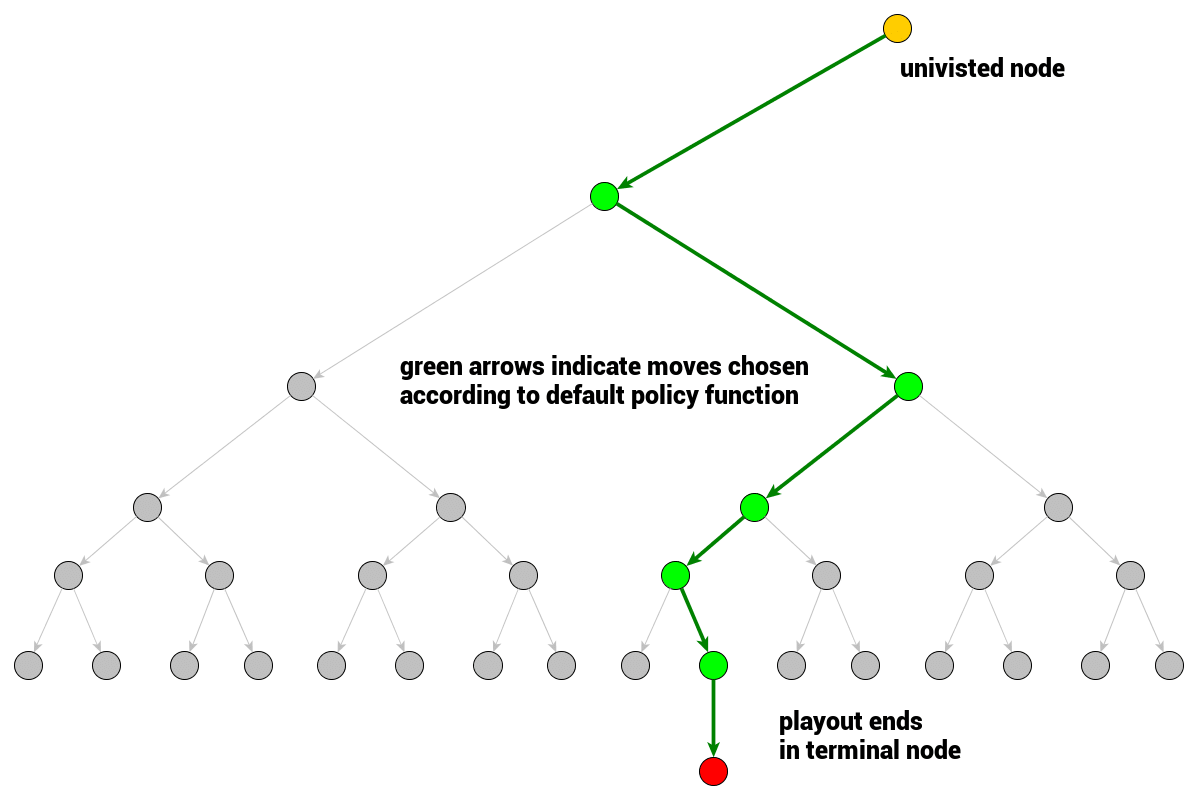
模拟的最简单的形式只是一个从给定游戏状态到终端的随机移动序列。模拟总是会产生一个结果，对于游戏来说就是获胜、失败或平局，但是广义上来说模拟的合法结果可以是任意值。

游戏树节点扩展——完全扩展和访问过的节点

先来让我们思考一下人类是如何进行围棋或国际象棋的。
　　给定一个根节点和游戏的规则，剩下的游戏树就可以推导出来了，所以我们可以不用将整个树都保存到内存中。在初始状态，我们位于游戏树的根节点，其他的节点都是未访问的。一旦我们考虑一步移动，就会想象这个动作会产生什么样的结果。
　　MCTS也是一样，节点分为访问过的和未访问过的。被访问过的节点意味着某个模拟过程是以它为起点的，即它至少被评估过一次。如果一个节点的所有子节点都被访问过了，那这个节点就称为是完全扩展的，否则就是未完全扩展的。

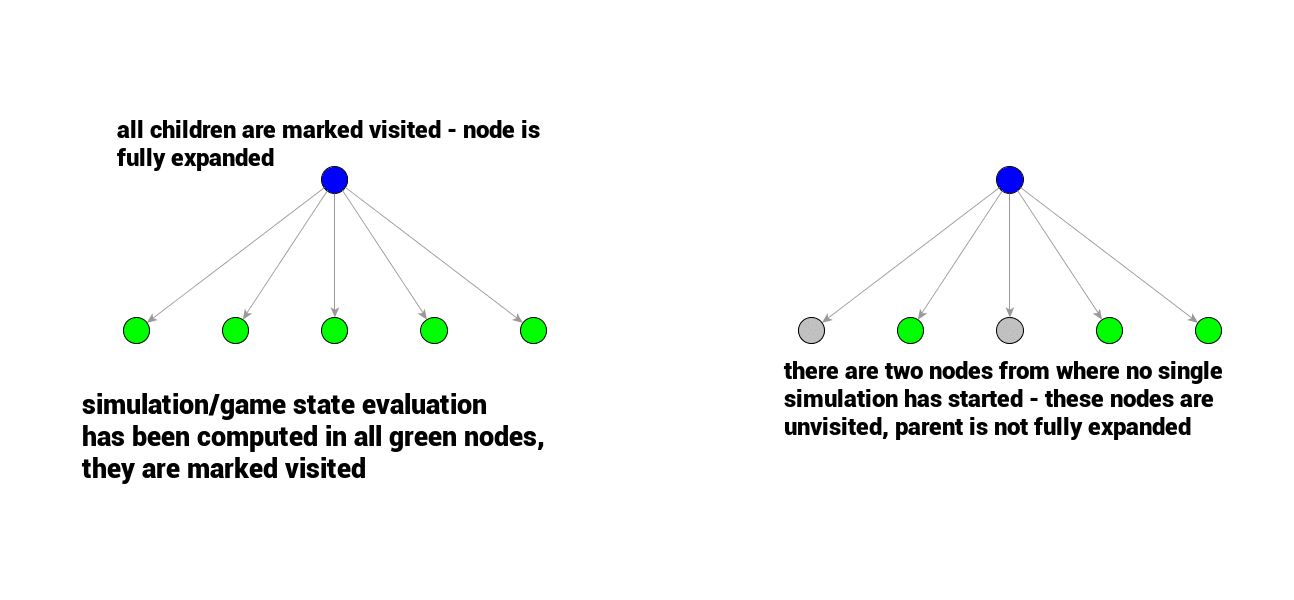
在实际应用中，搜索的一开始，根节点的所有子节点都是未被访问的，如果选择了一个，第一次模拟就随之开始。要注意的是，模拟过程中由rollout策略函数选择的节点是不会被标记为已访问过的，只有从模拟开始的节点被标记为已访问过。

反向传播

当完成对一个节点的模拟，其结果已准备好传播回当前游戏树的根节点，然后模拟开始的节点被标记为已访问。

反向传播是从叶节点（模拟开始）到根节点的遍历。模拟结果被传送到根节点，并更新反向传播路径上每个节点的统计信息。反向传播保证每个节点的统计信息能够反映该节点所有后代的模拟结果。

节点的统计信息

反向传播模拟结果的动机是为了更新反向传播路径上所有节点 $v$ （包括模拟开始的节点）的总模拟收益 $Q (v)$ 和总访问次数 $N (v)$ 。

$Q (v)$ ：总模拟收益是节点 $v$ 的一个属性，最简单形式的就是所有考虑的节点的模拟结果之和
$N (v)$ ：总访问次数是节点 $v$ 的另一个属性，代表这个节点有多少次出现在反向传播路径上

每个访问过的节点都需要维护这两个值。换句话说，如果你随机找一个节点，这个节点的统计信息反映了它多大可能是最佳下一步（总模拟收益），以及它被访问的频率（总访问次数）。收益高的节点是接下来探索的优秀候选节点，但那些访问次数低的节点也同样值得关注（因为它没有被探索完全）。

游戏树的遍历

在搜索的开始，因为我们还没有进行任何模拟，首先选择未遍历的节点。从每个节点开始一次模拟，模拟结果反向传播到根节点，然后根节点可以认为是完全扩展的。
　　但接下来怎么做呢？我们如何从一个完全展开的节点到一个未被访问的节点？我们需要遍历被访问过的节点的层，如何具体如何操作目前还没给出，大家耐心继续往下看。
　　为了选出我们路径上的下一个节点来开始下一次模拟，我们需要考虑 $v$ 的所有子节点 $v_1,v_2,...,v_k$ 的上的信息以及 $v$ 自身的信息。让我们来看看现在有哪些信息可以用:

我们当前节点（蓝色）是完全扩展的，所以它一定是被访问过的并且存储了相应的节点统计信息：总模拟收益和总访问次数，它的子节点也是一样。这些值组成了我们最后一个部分：树的置信度上界（Upper Confidence Bound applied to Trees，UCT）。

UCT

UCT是一个让我们从已访问的节点中选择下一个节点来进行遍历的函数，也是MCTS的核心函数。 $\mathbb{UCT}(v_i,v)=\frac{Q(v_i)}{N(v_i)}+c\sqrt{\frac{\log(N(v))}{N(v_i)}}\tag{2}$ MCTS遍历时，节点最大化UCT的值。现在让我们看看UCT函数做了什么：
　　首先，UCT函数是关于节点 $v$ 和其子节点 $v_i$ 的函数。它由两部分组成，第一部分是 $\frac{Q(v_i)}{N(v_i)}$ ，也称作exploitation component，可以看做是子节点 $v_i$ 的胜率估计（总收益/总次数=平均每次的收益）。看起来这一项已经有足够说服力，因为只要选择胜率高的下一步即可，但是为什么不能只用这一个成分呢？这是因为这种贪婪方式的搜索会很快导致游戏结束，这往往会导致搜索不充分，错过最优解。
　　举个简单的例子。现在假设MCTS的UCT函数只用了探索成分，从根节点开始，我们对所有子节点进行了一次模拟，然后在下一步中只访问至少赢了一次的子节点。那么在第一次模拟中那些不幸未被选中的节点（实际中rollout策略函数通常是随机的）将会被立刻抛弃，并再也得不到任何提升。因此有了UCT函数的第二项，称为exploration component。这个成分更倾向于那些想对较少被探索的节点（ $N(v_i)$ 较小）。让我们来看看UCT函数的exploration component的函数形状，它随访问次数的增加而下降，这可以使搜索过程朝那些较少访问的节点进行。

最后，式(2)中的参数 $c$ 是exploitation和exploration之间的折中系数。

MCTS的终止

现在，我们知道了成功实现MCTS的必要条件，但是仍有几个问题我们需要回答。首先，我们应该什么时候结束MCTS过程？答案是：它取决于上下文。如果你考虑搭建一个游戏引擎，那么你的“思考时间”可能是有限的，计算能力也是有限的。因此最保险的做法是在你资源允许的情况下尽可能久地运行MCTS。
　　当MSCT程序结束时，最佳的移动通常是访问次数最多的那个节点。

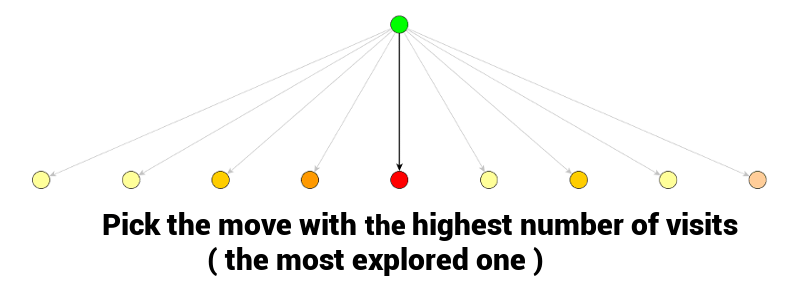
当你使用MCTS选择了移动之后，你选择的节点将变成你对手移动的游戏状态。当你对手选择了他的移动，你将再次从对手选择的节点处开始MCTS搜索。先前MCTS的一些统计信息可能仍然存在于你在正在考虑的新分支中，这样就可以不用重新构建树而是重用统计数据即可。