CKKS自举笔记（CKKS Bootstrapping）

CKKS的Bootstrapping技术在18年提出 ¹。CKKS无法使用常规的Bootstapping技术，即通过运行同态的解密电路来做噪声刷新，因为CKKS的解密电路仍然保留噪声，不像BGV和BFV那样完全消除噪声。

因此现在CKKS的Bootstrapping都是通过扩模的方法：将初始的密文$\mathsf{ct}$认为是在一个较小的模数$q$上面，其中$[⟨\mathsf{ct},\mathsf{sk}⟩{]}_q=m$。可以直接将其视为一个大模数$q_L$下面的密文$\mathsf{c}{\mathsf{t}}^{\prime }$，但$\mathsf{c}{\mathsf{t}}^{\prime }$包含的明文是$[⟨\mathsf{c}{\mathsf{t}}^{\prime },\mathsf{sk}⟩{]}_{q_L}=m+q\cdot I$，因此要通过一个取模的操作将$q\cdot I$消除。如何进行同态地取模是CKKS Bootstrapping的核心问题。

CKKS Bootstrapping流程

流程的框架

主要包含四步：扩模（ModRaise），同态编码（CoeffToSlot），同态取模（EvalMod），同态解码（SlotToCoeff）。

$$m(\mathrm{mod}q)\stackrel{\mathsf{ModRaise}}{\to }m+qI(\mathrm{mod}Q)\stackrel{\mathsf{CoeffToSlot}}{\to }(m+qI{)}^{\ast }\stackrel{\mathsf{EvalMod}}{\to }(m{)}^{\ast }\stackrel{\mathsf{SlotToCoeff}}{\to }m(\mathrm{mod}{Q}^{\prime })$$

扩模（ModRaise）：一个密文$\mathsf{ct}$包含的明文为$m(X)=[⟨\mathsf{ct},\mathsf{sk}⟩{]}_q$，则$t(X)=⟨\mathsf{ct},\mathsf{sk}⟩=qI(X)+m(X)\equiv m(X)\mathrm{mod}q$，其中$\Vert I(X){\Vert }_{\infty }<K=O(\sqrt{h})$。这里的$h$是$\mathsf{sk}$中1的数量。取一个足够大的模数$Q$，那么$[t(X){]}_Q=t(X)$。

Sparse Key 一般来说，同态加密中$\mathsf{sk}$中系数从$(-1,0,1)$中选取，每个系数选取到的概率相同，$n$位的密钥的$h=2/3n$。而在需要使用Bootstrapping的方案里面，会设定$h=64$，可以令$K$尽可能地小。但会导致安全性降低，因此要取比较大的$n$来保证安全性，这种密钥选取叫做稀疏密钥(Sparsed Key)。如何不基于稀疏密钥构造Bootstrapping也是一个研究点。

同态编码（CoeffToSlot）：我们要对多项式的系数进行一个取模操作，但我们使用同态的加法和乘法来拟合取模操作，而同态的加法和乘法是针对Slot中的数做的，因此，要将系数放进Slot中。相当于做一个同态的密文编码操作，可以使用乘DFT矩阵的方法来实现。但这里有一个问题，多项式的系数是$n$个，而明文Slot只有$n/2$个，因此这一步会得到两个密文分别加密$z_0^{\prime }=(t_0,...,t_{\frac{N}{2}-1})$和$z_1^{\prime }=(t_{\frac{N}{2}},...,t_{N-1})$。

同态取模操作（EvalMod）：使用加法和乘法来拟合取模操作，这一步会产生一定的噪声。因为加法和乘法执行过程有噪声，同时拟合函数本身使用了三角函数来对取模函数拟合，三角函数和取模之间还存在一定的误差，这一部分也会形成噪声。噪声的大小与消息和$q$之间的大小关系$ϵ=\frac{m}{q}$决定。因此，令$m$尽可能的小也是一种控制噪声的方法。

同态解码（SlotToCoeff）：同态解码操作是同态编码的逆操作。将Slot中的数放回系数中。也是通过一个矩阵乘法的方式来做。

总结：可以看到，CKKS的Bootstrapping都是直接在密文上进行操作，比如乘一个DFT矩阵和DFT逆矩阵，以及密文上面的多项式操作。因此，相比其他Bootstrapping技术存在的优势是：

1. 不需要Bootstrapping密钥
2. 计算复杂度是$O(\log (|sk{|}_1\cdot q))$的
3. 需要的内存很小，只有一个密文反复计算

如何做同态取模操作

取模操作$F(x)=[x{]}_q$本身并不是一个连续的周期函数，因此无法直接对取模操作进行多项式拟合。但是¹观察到由于$m<<q$，所以我们最终要拟合的部分只有以$q$为间隔的中间一小部分，因此，如下图所示，我们需要计算的部分只有黑色的直线区域，因此，可以使用一个三角函数$\sin$来进行拟合。这里拟合的范围是$[-Kq,Kq]$，原因在于$t(X)=⟨\mathsf{ct},\mathsf{sk}⟩=qI(X)+m(X)\equiv m(X)\mathrm{mod}q,\Vert I(X){\Vert }_{\infty }<K$。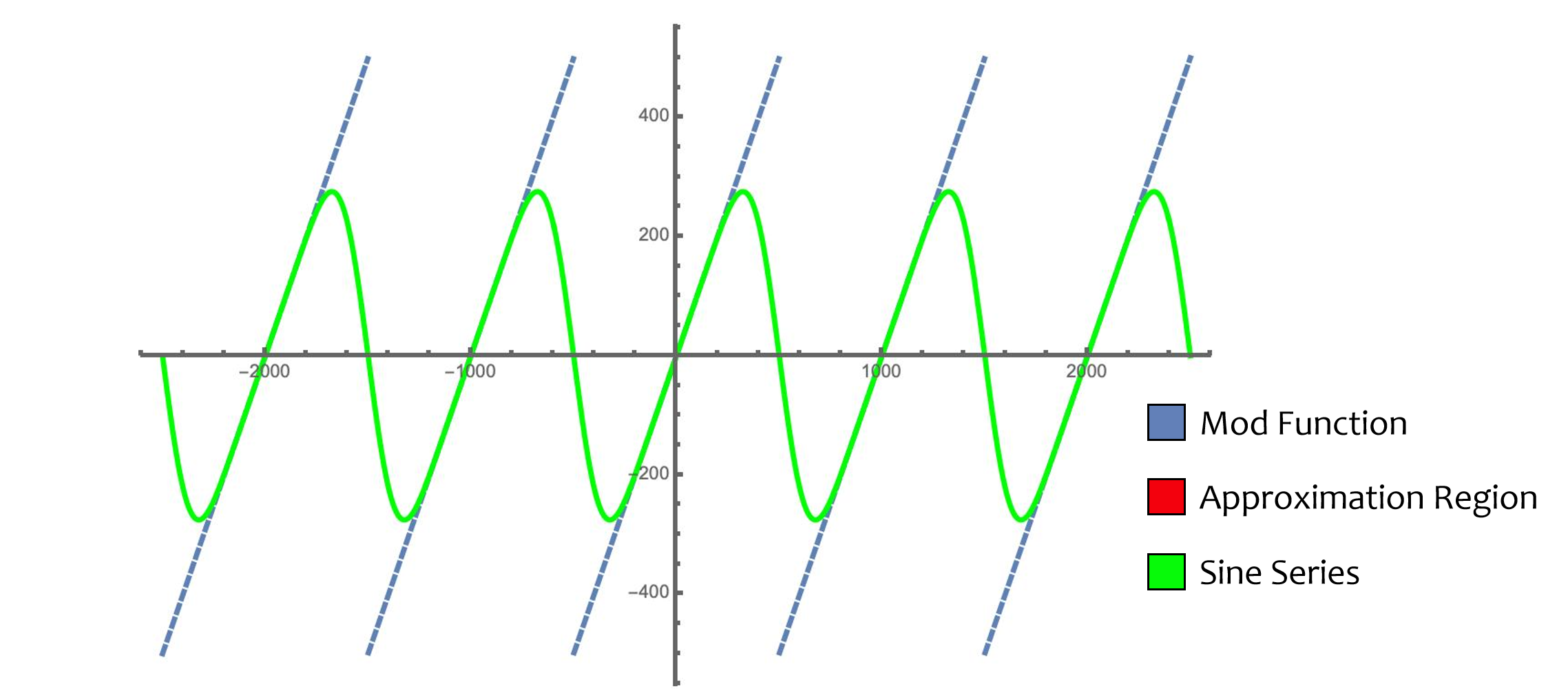

在欧密2018¹的方案中，直接采用了$S(x)=\frac{q}{2\pi }\sin (\frac{2\pi }{q}x)$函数对$[x{]}_q$函数进行拟合，但这个拟合函数这样最终会有大约$|[x{]}_q-S(x)|\le \frac{2{\pi }^2}{3}q{ϵ}^3\to O(q{ϵ}^3)$的误差，其中$ϵ=\frac{m}{q}$。

误差的推导为：(根据1阶泰勒展开式)
$$|[x{]}_q-S(x)|=\frac{q}{2\pi }\left|\frac{2\pi m}{q}-\sin \left(\frac{2\pi m}{q}\right)\right|\le \frac{q}{2\pi }\cdot \frac{1}{3!}{\left(\frac{2\pi |m|}{q}\right)}^3=O\left(q\cdot \frac{|m{|}^3}{q^3}\right)=O(q{ϵ}^3)$$

$\sin (x)$的泰勒展开式为$\sin x={\sum }_{n=0}^{\infty }\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}$

直接泰勒展开（naive idea）

一个很直接的想法来拟合$S(x)$是通过泰勒展开为一个高次的多项式，然后采用Paterson-Stockmeyer方法²来运算这个多项式。

泰勒展开多项式拟合

泰勒展开式：
$$f(x)=\sum _{j=0}^{d-1}\frac{f^{(n)}(x_0)}{d!}\cdot (x-x_0{)}^d$$
我们要执行函数$[x{]}_q$的定义域是$[-Kq,Kq]$，这里的$K=O(\lambda )$。我们可以直接对$S(x)$执行泰勒展开，得到
$$S^{\prime }(x)=\frac{q}{2\pi }\sum _{j=0}^{d-1}\frac{(-1{)}^j}{(2j+1)!}{\left(\frac{2\pi x}{q}\right)}^{2j+1}$$
因为$|x|<Kq$，所以其中$|S(x)-S^{\prime }(x)|<\frac{q}{2\pi }\cdot \frac{1}{(2d+1)!}(2\pi K{)}^{2d+1}$。

可以用斯特灵公式[^ strling]进行一个推导：$n!\sim \sqrt{2 \pi n}\left(\frac{n}{e} \right)^n $。
$$\frac{q}{2\pi }\cdot \frac{1}{(2d+1)!}(2\pi K{)}^{2d+1}=\frac{q}{2\pi }\cdot \frac{{(2\pi eK)}^{2d+1}}{\sqrt{2\pi (2d+1)}\cdot (2d+1{)}^{2d+1}}$$
当我们取到阶为$d=O(Kq)$时，这个误差就足够小到可以忽略了。

我们可以用Paterson-Stockmeyer方法²来用$O(\sqrt{d})=O(\sqrt{Kq})$次的乘法来运算这个多项式。

Paterson-Stockmeyer方法计算多项式

Paterson-Stockmeyer方法可以用$O(\sqrt{n})$次乘法执行$n$次多项式，具体如下：对于一个$n$阶多项式$F(x)={\sum }_{i=0}^{n-1}{a}_i{x}^i$，令$n=k\cdot m$，
$$\begin{array}{rl}F(x)& =a_{km-1}{x}^{km-1}+\cdots +a_{1}x+a_0\\ & =(a_{km-1}{x}^{k-1}+\cdots +a_{k(m-1)})\cdot x^{k(m-1)}\\ & +(a_{k(m-1)-1}{x}^{k-1}+\cdots +a_{k(m-2)})\cdot x^{k(m-2)}\\ & ...\\ & +(a_{2k-1}{x}^{k-1}+\cdots +a_k)\cdot x^k\\ & +a_{k-1}{x}^{k-1}+\cdots +a_0.\end{array}$$
我们需要算的是$x^1,x^2,...,x^k$的$k$次乘法，$x^{2k},...,x^{(m-1)k}$的$m$次乘法，以及$m$行中每一行的一次乘法，当$k=\sqrt{n}$的时候，乘法的次数最优。

但就算如此还是需要$O(\sqrt{Kq})$次的乘法，仍然是非常大的计算量。

采用二倍角公式来拟合（欧密2018）

直接泰勒展开存在的问题是：
$$S(x)=\frac{q}{2\pi }sin\left(\frac{2\pi x}{q}\right)\approx S^{\prime }(x)=\frac{q}{2\pi }\sum _{j=0}^{d-1}\frac{(-1{)}^j}{(2j+1)!}{\left(\frac{2\pi x}{q}\right)}^{2j+1}$$
需要取到$d=O(Kq)$时才可以保证$S^{\prime }(x)-S(x)$足够小。乘法的次数就算使用了²中的方法还是太大了。

我们可以考虑用二倍角公式来构造一个$O(\log d)$复杂度的拟合方法¹。

注意到在欧拉公式中，$\exp (i\theta )=\cos (\theta )+i\cdot \sin (\theta )$，可以得出$\sin (\theta )=\frac{1}{2}i\cdot \left(\exp (i\theta )-\exp (-i\theta )\right)$。

因此可以通过$\exp (\frac{i2\pi x}{q})$来得到$\sin (\frac{2\pi x}{q})$。

而$\exp (\frac{i2\pi x}{q})$函数可以通过递归$\exp (\frac{i2\pi x}{2^{r}q})$的平方来得到，原因如下：
$$\{\begin{array}{rl}& \exp (i\theta )=\cos \theta +i\sin \theta ,\\ & \exp (2i\theta )=(\exp (i\theta ){)}^2,\end{array}\leftarrow \{\begin{array}{rl}& \cos (2\theta )={\cos }^2\theta -{\sin }^2\theta ,\\ & \sin (2\theta )=2\cos \theta \cdot \sin \theta .\end{array}$$
完整的调用流程如下：

最初是用$P_0(t)$来拟合$\exp \left(\frac{2\pi it}{2^r\cdot q}\right)$，由于取值范围比较小，因此只要取到一个很小的阶$d_0$就可以令误差足够小。然后通过不断取平方的方式来得到$\exp (\frac{2\pi it}{q})$。

初始的噪声为：
$$|P_0(t)-\Delta \cdot \exp \left(\frac{2\pi it}{2^r\cdot q}\right)|\le \frac{\Delta }{(d_0+1)!}|\frac{2\pi K}{2^r}{|}^{d_0+1}$$

平方$r$次之后的噪声为：
$$\begin{array}{rl}\left|P_r(t)-\Delta \cdot \exp \left(\frac{2\pi it}{q}\right)\right|& \le \frac{\Delta \cdot 2^r}{\left(d_0+1\right)!}{\left(\frac{2\pi K}{2^r}\right)}^{d_0+1}\\ & \le \frac{\Delta \cdot 2^r}{\sqrt{2\pi \left(d_0+1\right)}}{\left(\frac{e\pi K}{2^{r-1}\left(d_0+1\right)}\right)}^{d_0+1}\end{array}$$
因此从参数选取上来说，只要选$d_0=O(1),r=O(\log (Kq))$就可以让噪声足够小。

在计算出$\exp \left(\frac{2\pi it}{2^r\cdot q}\right)$之后，可以运算$\sin (\frac{2\pi m}{q})=\frac{1}{2}i\cdot \left(\exp \left(\frac{2\pi im}{q}\right)-\exp \left(\frac{-2\pi im}{q}\right)\right)$

如何做同态编码或解码

CKKS的编码和解码基础知识（明文下面怎么做）

对一个2的幂次的数$M$来说，第$M$个分圆多项式为${\Phi }_M(X)=X^N+1$，将数字$5$作为生成元，可以构成了一个阶为$N/2$的模$M$的乘5循环群 { 5 j   m o d   M ∣ j ∈ [ 0 , N / 2 ] } \{5^j \bmod M| j\in[0,N/2]\} { 5jmodM∣j∈[0,N/2]}，此外，这个群乘$-1$也构成一个乘5的循环群 { − 5 j   m o d   M ∣ j ∈ [ 0 , N / 2 ] } \{-5^j \bmod M |j\in [0,N/2]\} { −5jmodM∣j∈[0,N/2]}，这两个乘法群可以构成完整的$Z_M^{\ast }$。

举例，对于$M=16$来说，两个阶为$4$的乘法群分别为$[1,5,9,13],[15,11,7,3]$。

因此，对于${\Phi }_M(X)=X^N+1$的某个$M$次单位原根$\zeta$来说，可以令${\zeta }_j={\zeta }^{5^j},0\le j<N/2$。$\left{\zeta_{j}, \overline{\zeta_{j}}: 0 \leq j<N / 2\right} $组成了单元原根的集合。

举例，对于$X^8+1$来说:

${\zeta }_0=\zeta ,{\zeta }_1={\zeta }^5,{\zeta }_2={\zeta }^9,{\zeta }_3={\zeta }^{13}$，

$\overline{{\zeta }_0}={\zeta }^{15},\overline{{\zeta }_1}={\zeta }^{11},\overline{{\zeta }_2}={\zeta }^7,\overline{{\zeta }_3}={\zeta }^3$。

对于同态的解码是将系数形式多项式变为点值形式；而编码是将点值形式变为系数形式。

CKKS支持将$N/2$个复数${\mathbb{C}}^{N/2}$编码到一个实系数多项式$R=\mathbb{R}(X)/{\Phi }_M(X)$。

对于一个系数多项式$m(X)$来说，$m(X)={\sum }_{i=0}^{N-1}{m}_i{X}^i$，可以令其系数组成向量$\mathbf{m}=(m_0,...,m_{N-1})$。

解码函数：$\tau :R\to {\mathbb{C}}^{N/2}$，比如$\tau :m(X)\to \mathbf{z}=(z_j{)}_{0\le j<N/2}$，那么$z_j=m({\zeta }_j)={\sum }_{i=0}^{N-1}{m}_i\cdot ({\zeta }_j{)}^i$。

因此，这个解码变换可以写为$\mathbf{z}=\mathbf{U}\cdot \mathbf{m}$，其中$\mathbf{U}$为：
$$\mathbf{U}=\left[\begin{array}{ccccc}1& {\zeta }_0& {\zeta }_0^2& \cdots & {\zeta }_0^{N-1}\\ 1& {\zeta }_1& {\zeta }_1^2& \cdots & {\zeta }_1^{N-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\zeta }_{\frac{N}{2}-1}& {\zeta }_{\frac{N}{2}-1}^2& \cdots & {\zeta }_{\frac{N}{2}-1}^{N-1}\end{array}\right]\in {\mathbb{C}}^{(N/2)\times N}$$
**编码函数：**直接取解码函数的逆变换，其实$\mathbf{m}={\mathbf{U}}^{-1}\cdot \mathbf{z}$。但${\mathbf{U}}^{-1}$一般不直接计算，利用范德蒙的行列式的形式，我们将$\mathbf{U}$进行扩充，令$\mathsf{CRT}=\left[\begin{array}{rl}& U\\ & \overline{U}\end{array}\right]$，那么$(\mathbf{z},\overline{\mathbf{z}})=\mathsf{CRT}\cdot \mathbf{m}$，则$\mathbf{m}={\mathsf{CRT}}^{-1}\cdot (\mathbf{z},\overline{\mathbf{z}})$。

其中${\mathsf{CRT}}^{-1}=\frac{1}{N}{\overline{\mathsf{CRT}}}^T=\frac{1}{N}({\overline{U}}^T,U^T)$。

因此这个逆变换可以写为：$\mathbf{m}=\frac{1}{N}({\overline{U}}^T\cdot \mathbf{z}+U^T\cdot \overline{\mathbf{z}})$。

同态的旋转、共轭，和同态矩阵向量乘法（密文状态下怎么做）

在计算编码函数的时候，相当于要计算密文状态下的$\mathbf{m}=\frac{1}{N}({\overline{U}}^T\cdot \mathbf{z}+U^T\cdot \overline{\mathbf{z}})$过程，解码函数为$\mathbf{z}=U\cdot \mathbf{m}$。其中$U$是明文输入，$\mathbf{z}$是密文，$\mathbf{m}$是密文，因此要找到密文状态下做矩阵乘法和密文做共轭的操作。就可以在密文状态下做同态的编码和解码了。

旋转和共轭操作是使用密钥转化(KeySwitch)算法来构造的，

同态密钥转换

简单来说KeySwitch算法可以将一个由$s^{\prime }$加密的密文$c{t}^{\prime }$，其中包含的明文信息为$m$，转换为一个由$s$加密的密文$ct$，其中包含的明文信息为$m$。

KeySwitch过程为：

首先，密文$c{t}_1=(b_1,a_1)$，其中$b_1+a_1{s}^{\prime }=m+e_1$。

转化密钥的生成过程$\mathsf{ksk}\leftarrow {\mathsf{KSGen}}_s(s^{\prime })$：取$a^{\prime }\in {\mathcal{R}}_{PQ}$，$b^{\prime }=-a^{\prime }s+e^{\prime }+P{s}^{\prime }\mathrm{mod}PQ$，转化密钥为$(b^{\prime },a^{\prime })$。

密钥转化的过程$ct\leftarrow \mathsf{KeySwitch}(c{t}_1,\mathsf{ksk})$：$(b,a)=(b_1,0)+\lfloor P^{-1}\cdot a_1\cdot \mathsf{ksk}\rfloor \mathrm{mod}Q$。

那么得到的$ct$是由$s$加密的$m$构成的密文，正确性推导如下：
$$\begin{array}{rl}b+as& =b_1+\lfloor P^{-1}\cdot a_1\cdot b^{\prime }\rfloor +(\lfloor P^{-1}\cdot a_1\cdot a^{\prime }\rfloor )s\\ & =b_1+P^{-1}\cdot a_1\cdot (-a^{\prime }s+e^{\prime }+P{s}^{\prime })+P^{-1}{a}_1{a}^{\prime }s+ϵ\\ & =b_1+a_1{s}^{\prime }+P^{-1}{a}_1{e}^{\prime }+ϵ\\ & =m+e_1+P^{-1}{a}_1{e}^{\prime }+ϵ\\ & \approx m\end{array}$$

同态的旋转和共轭

考虑明文多项式如何旋转Slot：

在编码过程中，对于一个向量$\mathbf{z}=(z_j{)}_{0\le j<\frac{N}{2}}$来说，将其编码为多项式$m(X)$的方式是将$\mathbf{z}$放入$m(X)$的点值表达式中，点值对应的横坐标为${\zeta }^{5^j}$，比如对于$N=8$时，点值的横坐标为$[\zeta ,{\zeta }^5,{\zeta }^9,{\zeta }^{13}]$。即$m({\zeta }^{5^i})=z_i$，而在共轭的位置会放$\overline{z_i}$，即$m(\overline{{\zeta }^{5^i}})=\overline{z_i}$。

如果我们要将其左移两位，则可以计算${\phi }_2(x)=x^{5^2}:{\zeta }_j\to {\zeta }_j^{5^2}$，则${\phi }_2(m(X))$所对应的横坐标为$[{\zeta }^9,{\zeta }^{13},\zeta ,{\zeta }^5]$。那么其对应的明文为$(z_2,z_3,z_0,z_1)$，也就是左移了两位。

密文通过KeySwitch旋转：

对于一个密文来说，$\mathsf{ct}=(b,a)$，其中$b+as=m+e$，我们要得到$\phi (m)$，可以计算$\phi (\mathsf{ct})=(\phi (b),\phi (s))$。

$\phi (\mathsf{ct})$是由$\phi (s)$加密的$\phi (m)$：$\phi (b)+\phi (a)\cdot \phi (s)=\phi (m)+\phi (e)$。

所以我们在密文$\mathsf{ct}$上进行了$\phi (\cdot )$变化后，可以通过KeySwitch将其变为由$s$加密的$\phi (m)$，也就实现了旋转。

令${\mathsf{rk}}_r={\mathsf{KSGen}}_s({\phi }_r(s))$

$\mathsf{Rot}(\mathsf{ct};r):\mathsf{KeySwitch}(\phi (\mathsf{ct}),{\mathsf{rk}}_r)$。

通过KeySwitch求共轭：

共轭的思想和旋转一致，只是将$\phi$函数替换为${\phi }^{\prime }(x):x^{-1}$。

比如$[\zeta ,{\zeta }^5,{\zeta }^9,{\zeta }^{13}]$变为了$[{\zeta }^{15},{\zeta }^{11},{\zeta }^7,{\zeta }^3]$。对应了共轭操作。

同态的矩阵向量乘法

记$k=N/2$，对于一个矩阵$A=\left[\begin{array}{ccccc}{A}_{0,0}& A_{0,1}& A_{0,2}& \cdots & A_{0,k-1}\\ A_{1,0}& A_{1,1}& A_{1,2}& \cdots & A_{1,k-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ A_{k-1,0}& A_{k-1,1}& A_{k-1,2}& \cdots & A_{k-1,k-1}\end{array}\right]\in {\mathbb{C}}^{k\times k}$

对于一个向量$\mathbf{z}=(z_j{)}_{0\le j<k}$来说，我们要计算 m = A z = { ∑ i = 0 k − 1 A i , j z j } i \boldsymbol{m}=A\boldsymbol{z}= \{\sum_{i=0}^{k-1}A_{i,j}z_j\}_i m=Az={ ∑i=0k−1​Ai,j​zj​}i​。其中$A$是明文，$\mathbf{z}$是密文。

难点在于：$\mathbf{z}$是密文状态，而且要在打包的情况下计算。打包支持的乘法运算是向量两两之间的相乘（点乘），而矩阵乘法其实每行做了一个内积。所以如何在明文打包的情况下，通过向量两两之间的乘法，来构造一个矩阵乘法是一个难点。

初始思路：

两两之间的乘法其实也存在，

我们可以取第一列元素 { A 0 , 0 , A 1 , 0 , . . . , A k − 1 , 0 } \{A_{0,0},A_{1,0},...,A_{k-1,0}\} { A0,0​,A1,0​,...,Ak−1,0​}，与向量 { z 0 , z 0 , . . . z 0 } \{z_0,z_0,...z_0\} { z0​,z0​,...z0​}之间两两相乘（点乘），

第二列元素 { A 0 , 1 , A 1 , 1 , . . . , A k − 1 , 1 } \{A_{0,1},A_{1,1},...,A_{k-1,1}\} { A0,1​,A1,1​,...,Ak−1,1​}与向量 { z 1 , z 1 , . . . , z 1 } \{z_1,z_1,...,z_1\} { z1​,z1​,...,z1​}之间两两相乘，

…

然后将这些结果的向量累加起来，就可以得到 { ∑ i = 0 k − 1 A 0 , i z i , ∑ i = 0 k − 1 A 1 , i z i , . . . ∑ i = 0 k − 1 A k − 1 , i z i } \{\sum_{i=0}^{k-1}A_{0,i}z_i, \sum_{i=0}^{k-1}A_{1,i}z_i,...\sum_{i=0}^{k-1}A_{k-1,i}z_i\} { ∑i=0k−1​A0,i​zi​,∑i=0k−1​A1,i​zi​,...∑i=0k−1​Ak−1,i​zi​}。

但这样的话，我们需要$k$个密文，分别加密 { z i , . . . , z i } 0 ≤ i < k \{z_i,...,z_i\}_{0\le i < k} { zi​,...,zi​}0≤i<k​。

改善思路：

注意到，

1. 原本在矩阵第$i$行的元素，被累加到了结果向量的第$i$个位置。所以我们要构造的向量要满足 { A 0 , r , A 1 , r ′ , . . . , A k − 1 , r ′ ′ } \{A_{0,r},A_{1,r'},...,A_{k-1,r''}\} { A0,r​,A1,r′​,...,Ak−1,r′′​}的形式。

2. 而第$j$列对应的元素，要与$z_j$相乘。而$\mathbf{z}=(z_0,...,z_{k-1})$本身是一个下标递增的数组。

所以我们要构造的与$\mathbf{z}$进行的点乘的数组，可以取 a i = { A 0 , i , A 1 , i + 1 , . . . , A k − i , 0 , . . . , A k − 1 , i − 1 } \boldsymbol{a}_i=\{A_{0,i},A_{1,i+1},...,A_{k-i,0},...,A_{k-1,i-1}\} ai​={ A0,i​,A1,i+1​,...,Ak−i,0​,...,Ak−1,i−1​}，与${\mathbf{z}}_i=(z_i,z_{i+1},...,x_{k-i,0}...,z_{i-1})$相乘。

${\mathbf{z}}_i$可以通过将$\mathbf{z}$左移$i$位来构造${\mathbf{z}}_i=\mathsf{Rot}(\mathbf{z},i)$。${\mathbf{a}}_i$是直接取$A$的第$i$个对角线向量。

因此：$A\cdot \mathbf{z}={\sum }_{0\le i<k}({\mathbf{a}}_i\cdot \mathsf{Rot}(\mathbf{z},i))$。其中

这样的话，只需要原本的$\mathbf{z}$的密文就可以构造。但需要$k$次的旋转和$k$次的明文密文乘法。但旋转操作比较耗时，有没有方法进一步减少旋转的次数？是有的：

小步大步法：

取$k_1\cdot k_2=k$
$$\begin{array}{rl}A\cdot \mathbf{z}& =\sum _{0\le i<k}({\mathbf{a}}_i\cdot \mathsf{Rot}(\mathbf{z},i))\\ & =\sum _{0\le j<k_2}\sum _{0\le i<k_1}({\mathbf{a}}_{j\cdot k_1+i}\cdot \mathsf{Rot}(\mathbf{z},j\cdot k_1+i))\\ & =\sum _{0\le j<k_2}\mathsf{Rot}\left(\sum _{0\le i<k_1}\mathsf{Rot}(a_{j\cdot k_1+i},-j\cdot k_1)\cdot \mathsf{Rot}(\mathbf{z},i),j\cdot k_1\right)\end{array}$$
这样做就只需要$k_1+k_2=\sqrt{k}$次的旋转，$k_1\cdot k_2=k$次的乘法。

CKKS BootStrapping方案整体(将上面提到的方法结合一下)

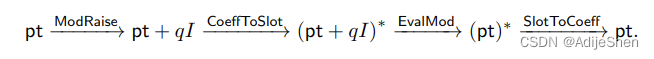
扩模（ModRaise）：一个模数为$q$的密文$\mathsf{ct}$包含的明文为$m(X)=[⟨\mathsf{ct},\mathsf{sk}⟩{]}_q$，则$t(X)=⟨\mathsf{ct},\mathsf{sk}⟩=qI(X)+m(X)\equiv m(X)\mathrm{mod}q$，其中$\Vert I(X){\Vert }_{\infty }<K=O(\sqrt{h})$。这里的$h$是$\mathsf{sk}$中1的数量。因此，$\mathsf{ct}$可以认为是一个大模数为$Q_0\gg q$的密文，其中包含的明文为$t(X)=t_0+t_{1}X+\cdots +t_{N-1}{X}^{N-1}$。

同态编码（CoeffToSlot）：我们要对多项式的系数进行一个取模操作，但我们使用同态的加法和乘法来拟合取模操作，而同态的加法和乘法是针对Slot中的数做的，因此，要将系数放进Slot中。相当于做一个同态的密文编码操作，可以使用乘DFT矩阵的方法来实现。但这里有一个问题，多项式的系数是$n$个，而明文Slot只有$n/2$个，因此这一步会得到两个密文分别加密$z_0^{\prime }=(t_0,...,t_{\frac{N}{2}-1})$和$z_1^{\prime }=(t_{\frac{N}{2}},...,t_{N-1})$。
$$U=\left[\begin{array}{ccccc}1& {\zeta }_0& {\zeta }_0^2& \cdots & {\zeta }_0^{N-1}\\ 1& {\zeta }_1& {\zeta }_1^2& \cdots & {\zeta }_1^{N-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\zeta }_{\frac{N}{2}-1}& {\zeta }_{\frac{N}{2}-1}^2& \cdots & {\zeta }_{\frac{N}{2}-1}^{N-1}\end{array}\right]\in {\mathbb{C}}^{(N/2)\times N}$$
我们将其分为两块：
$$U_0=\left[\begin{array}{cccc}1& {\zeta }_0& \dots & {\zeta }_0^{\frac{N}{2}-1}\\ 1& {\zeta }_1& \dots & {\zeta }_1^{\frac{N}{2}-1}\\ ⋮& ⋮& \ddots & ⋮\\ 1& {\zeta }_{\frac{N}{2}-1}& \dots & {\zeta }_{\frac{N}{2}-1}^{\frac{N}{2}-1}\end{array}\right]\text{ and }{U}_1=\left[\begin{array}{cccc}{\zeta }_0^{\frac{N}{2}}& {\zeta }_0^{\frac{N}{2}+1}& \dots & {\zeta }_0^{N-1}\\ {\zeta }_1^{\frac{N}{2}}& {\zeta }_1^{\frac{N}{2}+1}& \dots & {\zeta }_1^{N-1}\\ ⋮& ⋮& \ddots & ⋮\\ {\zeta }_{\frac{N}{2}-1}^{\frac{N}{2}}& {\zeta }_{\frac{N}{2}-1}^{\frac{N}{2}+1}& \dots & {\zeta }_{\frac{N}{2}-1}^{N-1}\end{array}\right]$$
令${\mathbf{z}}^{\prime }\in {\mathbb{C}}^{N/2}$为密文$\mathsf{ct}$中的Slot内元素，可以得到${\mathbf{z}}_k^{\prime }=\frac{1}{N}\left({\overline{U_k}}^T\cdot {\mathbf{z}}^{\prime }+U_k^T\cdot \overline{{\mathbf{z}}^{\prime }}\right),k=0,1$。这一步可以使用上面的同态矩阵乘法来构造。

${\mathbf{z}}_k^{\prime }=\frac{1}{N}\left({\overline{U_k}}^T\cdot {\mathbf{z}}^{\prime }+U_k^T\cdot \overline{{\mathbf{z}}^{\prime }}\right),k=0,1$的正确性推导：

我们记$t(X)$的系数组成的列向量为$\mathbf{t}=(t_0,t_1,...,t_{N-1})$。

记${\mathbf{z}}^{\prime }=(z_0,...,z_{\frac{N}{2}-1})$为$t(X)$对应的点值（Slot内元素），因此$t({\zeta }_i)=z_i,0\le i<\frac{N}{2}$，$t(\overline{{\zeta }_i})=\overline{z_i}$。

因此${\mathbf{z}}^{\prime }=U\cdot \mathbf{t},\overline{{\mathbf{z}}^{\prime }}=\overline{U}\cdot \mathbf{t}$。
$$\begin{gathered} \left[\begin{array}{c}{\mathbf{z}}^{\prime }\\ \overline{{\mathbf{z}}^{\prime }}\end{array}\right]=\left[\begin{array}{cc}{U}_0& U_1\\ \overline{U_0}& \overline{U_1}\end{array}\right]\cdot \mathbf{t} \\ \to \left[\begin{array}{c}{\mathbf{z}}^{\prime }\\ \overline{{\mathbf{z}}^{\prime }}\end{array}\right]=\left[\begin{array}{cc}{U}_0& U_1\\ \overline{U_0}& \overline{U_1}\end{array}\right]\cdot \left[\begin{array}{c}{\mathbf{z}}_0^{\prime }\\ {\mathbf{z}}_1^{\prime }\end{array}\right]; \\ downarrow \\ \left[\begin{array}{c}{\mathbf{z}}_0^{\prime }\\ {\mathbf{z}}_1^{\prime }\end{array}\right]={\left[\begin{array}{cc}{U}_0& U_1\\ \overline{U_0}& \overline{U_1}\end{array}\right]}^{-1}\cdot \left[\begin{array}{c}{\mathbf{z}}^{\prime }\\ \overline{{\mathbf{z}}^{\prime }}\end{array}\right] \\ \to \left[\begin{array}{c}{\mathbf{z}}_0^{\prime }\\ {\mathbf{z}}_1^{\prime }\end{array}\right]=\frac{1}{N}\left[\begin{array}{cc}{\overline{U_0}}^T& U_0^T\\ {\overline{U_1}}^T& U_1^T\end{array}\right]\cdot \left[\begin{array}{c}{\mathbf{z}}^{\prime }\\ \overline{{\mathbf{z}}^{\prime }}\end{array}\right] \\ \downarrow \\ {\mathbf{z}}_0^{\prime }=\frac{1}{N}\left({\overline{U_0}}^T\cdot {\mathbf{z}}^{\prime }+U_0^T\cdot \overline{{\mathbf{z}}^{\prime }}\right) \\ {\mathbf{z}}_1^{\prime }=\frac{1}{N}\left({\overline{U_1}}^T\cdot {\mathbf{z}}^{\prime }+U_1^T\cdot \overline{{\mathbf{z}}^{\prime }}\right) \end{gathered}$$

同态取模操作（EvalMod）：在两个密文上分别运算$\frac{q}{2\pi }sin\left(\frac{2\pi x}{q}\right)$函数，过程为拟合$\exp \left(\frac{2\pi it}{2^r\cdot q}\right)$函数，通过不断将其平方，来计算$\exp \left(\frac{2\pi it}{q}\right)$，最后通过取共轭来得到$\exp \left(\frac{-2\pi it}{q}\right)$，可以运算$\frac{q}{2\pi }\sin (\frac{2\pi m}{q})=\frac{q}{2\pi }\cdot \frac{1}{2}\left(\exp \left(\frac{2\pi im}{q}\right)-\exp \left(\frac{-2\pi im}{q}\right)\right)$。

迭代运算过程如下：

同态解码（SlotToCoeff）：同态解码操作是同态编码的逆操作。将Slot中的数放回系数中。也是通过一个矩阵乘法的方式来做。

我们通过上一个同态取模操作，将$z_0^{\prime }=(t_0,...,t_{\frac{N}{2}-1})$和$z_1^{\prime }=(t_{\frac{N}{2}},...,t_{N-1})$变为了$z_0=(m_0,...,m_{\frac{N}{2}-1})$，$z_1=(m_{\frac{N}{2}},...,m_{N-1})$。我们计算$z=U_0\cdot z_0+U_1\cdot z_1$。

其余优化操作：

稀疏密文：不利用到密文中所有$N/2$个槽，而是z

原始方案的效果：

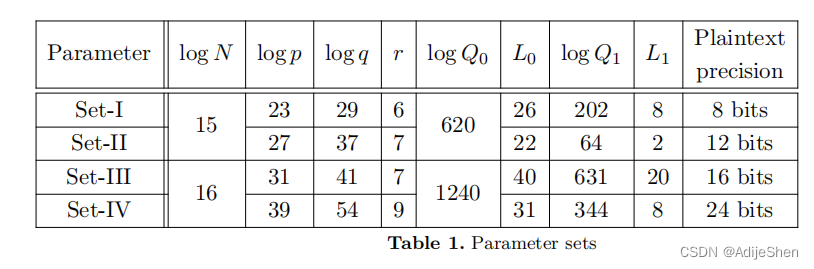
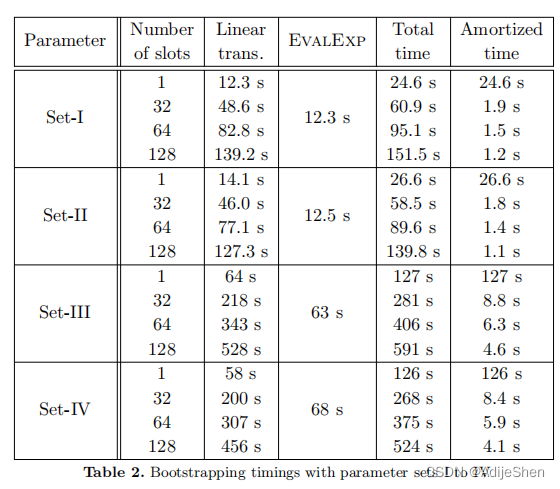
可以看出来这个初始的方案效果还是比较差的，精度24bit基本上无法运算了。

优化方案：

优化思路1：更改拟合函数(欧密2022a)

在上述的方案中，我们采用了$S(x)=\frac{q}{2\pi }sin\left(\frac{2\pi x}{q}\right)$函数来拟合$[x{]}_q$函数，但最终能够做到的精度只有16bit，非常的少。是因为这个函数本身与$[x{]}_q$之间存在着$O(q{ϵ}^3)$的误差。

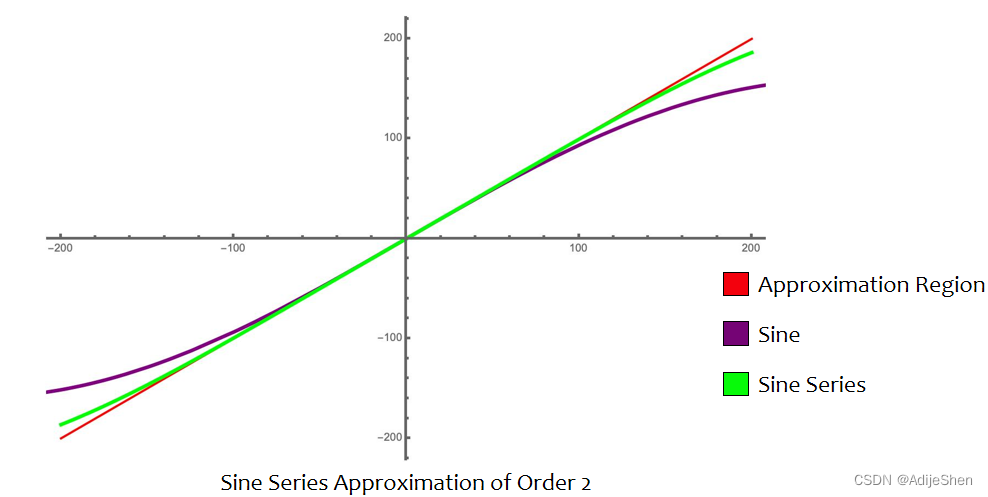
2022年欧密的一篇工作³发现了如果采用sine的序列，即$\frac{4}{3}\sin x-\frac{1}{6}\sin 2x$来计算的话，则可以达到更高的逼近程度。原因在于

$\sin x=x-x^3/3!+x^5/5!-x^7/7!+\dots$

$4/3\sin x=4/3x-2/9x^3+1/90x^5-1/3780x^7+\dots$

$-1/6\sin 2x=-1/3x+2/9x^3-2/45x^5+4/945x^7-\dots$

---

1. Jung Cheon, Kyoohyung Han, Andrey Kim, Miran Kim, and Yongsoo Song. Bootstrapping for approximate homomorphic encryption. In EUROCRYPT, pages 360–384, 01 2018. ↩︎ ↩︎ ↩︎ ↩︎

2. M. S. Paterson and L. J. Stockmeyer. On the number of nonscalar multiplications necessary to evaluate polynomials. SIAM Journal on Computing, 2(1):60–66, 1973.
   [^ strling]: 斯特林公式（Stirling’s approximation）https://blog.csdn.net/qq_40507857/article/details/82595516 ↩︎ ↩︎ ↩︎

3. Jutla, Charanjit S., and Nathan Manohar. “Sine series approximation of the mod function for bootstrapping of approximate HE.” Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Cham, 2022. ↩︎