文章目录
为什么会有这篇文章
在我参与工作的时候,这边就已经把CKKS的源码都写好了,没有能够自己实现一遍,导致目前对CKKS的Encoding方法一知半解。于是趁着有空来梳理一下。
首先看一下Daniel Huynh大佬的讲解,CKKS的上层框架。
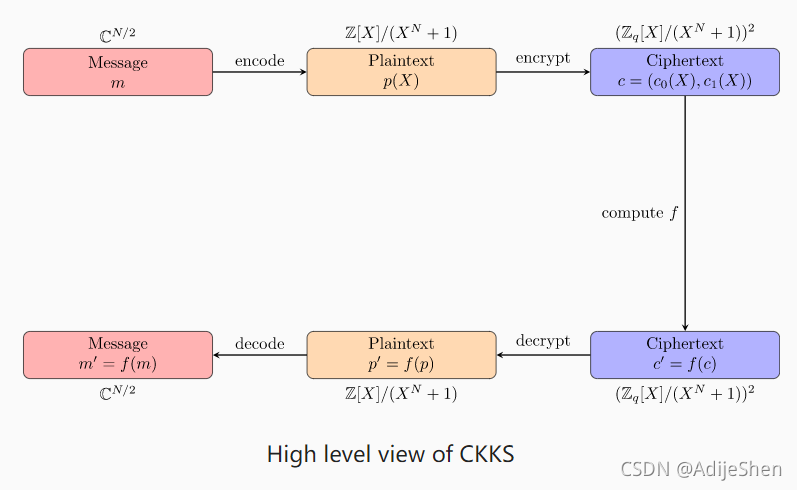
是将 N / 2 N/2 N/2个复数 m ∈ C N / 2 m\in \mathbb{C}^{N/2} m∈CN/2编码到一个 Z [ X ] / X N + 1 \mathbb{Z}[X]/X^N+1 Z[X]/XN+1的多项式 p ( x ) p(x) p(x)上,然后加密,得到 ( c 0 ( x ) , c 1 ( x ) ) ∈ ( Z q [ X ] / X N + 1 ) 2 (c_0(x),c_1(x))\in (\mathbb{Z}_q[X]/X^N+1)^2 (c0(x),c1(x))∈(Zq[X]/XN+1)2,同样有一个逆过程将一个密文变回 C N / 2 \mathbb{C}^{N/2} CN/2的向量。
要明白Encoding的过程,还需要先了解快速傅里叶变换(FFT)
快速傅里叶变换(FFT)
FFT思路
快速傅里叶变换可以看看这段视频https://www.youtube.com/watch?v=h7apO7q16V0
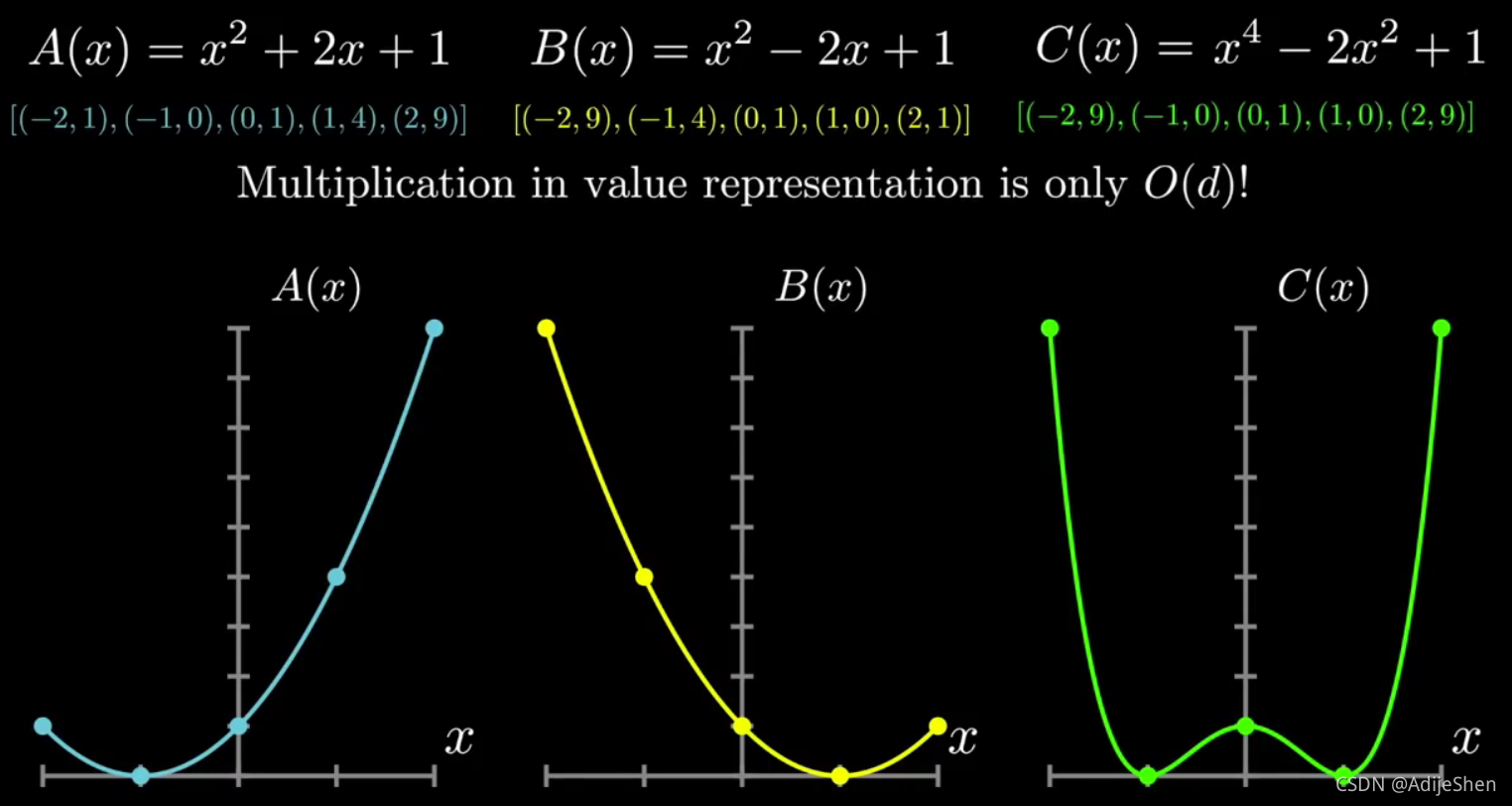
结合图片,来聊一下傅里叶变换的思路:
对于两个多项式
A ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a d x d , B ( x ) = b 0 + b 1 x + b 2 x 2 + ⋯ + b d x d A(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{d} x^{d},B(x)=b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{d} x^{d} A(x)=a0+a1x+a2x2+⋯+adxd,B(x)=b0+b1x+b2x2+⋯+bdxd
要计算他们的乘积
C ( x ) = c 0 + c 1 x + c 2 x 2 + ⋯ + c 2 d x 2 d C(x)=c_{0}+c_{1} x+c_{2} x^{2}+\cdots+c_{2 d} x^{2 d} C(x)=c0+c1x+c2x2+⋯+c2dx2d,
其中 c i = a 0 b i + a 1 b i − 1 + ⋯ + a i b 0 , i ∈ [ 0 , 2 d ] c_i=a_0b_i+a_1b_{i-1}+\cdots +a_ib_0,i\in[0,2d] ci=a0bi+a1bi−1+⋯+aib0,i∈[0,2d]。
因此,直接对多项式的系数进行运算的计算复杂度是 O ( d 2 ) O(d^2) O(d2)的。
然而
如果把这个多项式表示为点值形式,比如像图里一样,将 A ( x ) = x 2 + 2 x + 1 A(x)=x^2+2x+1 A(x)=x2+2x+1,表示为点值形式 [ ( − 2 , A ( − 2 ) ) , ( − 1 , A ( − 1 ) ) , ( 0 , A ( 0 ) ) , ( 1 , A ( 1 ) ) , ( 2 , A ( 2 ) ) ] [(-2,A(-2)),(-1,A(-1)),(0,A(0)),(1,A(1)),(2,A(2))] [(−2,A(−2)),(−1,A(−1)),(0,A(0)),(1,A(1)),(2,A(2))],那么就可以分别对点值进行两两相乘,得到 C ( x ) C(x) C(x)的点值表达形式: [ ( − 2 , A ( − 2 ) ⋅ B ( − 2 ) ) , ( − 1 , A ( − 1 ) ⋅ B ( − 1 ) ) , ( 0 , A ( 0 ) ⋅ B ( 0 ) ) , ( 1 , A ( 1 ) ⋅ B ( 1 ) ) , ( 2 , A ( 2 ) ⋅ B ( 2 ) ) ] [(-2,A(-2)\cdot B(-2)),(-1,A(-1)\cdot B(-1)),(0,A(0)\cdot B(0)),(1,A(1)\cdot B(1)),(2,A(2)\cdot B(2))] [(−2,A(−2)⋅B(−2)),(−1,A(−1)⋅B(−1)),(0,A(0)⋅B(0)),(1,A(1)⋅B(1)),(2,A(2)⋅B(2))]。由这样5个点,就可以唯一确定一个4次的多项式(见引理1)。而这样的两两相乘的运算复杂度只有 O ( d ) O(d) O(d)。
引理1: ( d + 1 ) (d+1) (d+1)个点值可以唯一确定一个 d d d阶多项式
{ ( x 0 , P ( x 0 ) ) , ( x 1 , P ( x 1 ) ) , … , ( x d , P ( x d ) ) } → P ( x ) = p 0 + p 1 x + p 2 x 2 + ⋯ + p d x d \left\{\left(x_{0}, P\left(x_{0}\right)\right),\left(x_{1}, P\left(x_{1}\right)\right), \ldots,\left(x_{d}, P\left(x_{d}\right)\right)\right\} \to P(x)=p_{0}+p_{1} x+p_{2} x^{2}+\cdots+p_{d} x^{d} { (x0,P(x0)),(x1,P(x1)),…,(xd,P(xd))}→P(x)=p0+p1x+p2x2+⋯+pdxd
可以把 P ( x 0 ) 到 P(x_0)到 P(x0)到 P ( x d ) P(x_d) P(xd)都列出来:
P ( x 0 ) = p 0 + p 1 x 0 + p 2 x 0 2 + ⋯ + p d x 0 d P ( x 1 ) = p 0 + p 1 x 1 + p 2 x 1 2 + ⋯ + p d x 1 d ⋮ P ( x d ) = p 0 + p 1 x d + p 2 x d 2 + ⋯ + p d x d d \begin{array}{c} P\left(x_{0}\right)=p_{0}+p_{1} x_{0}+p_{2} x_{0}^{2}+\cdots+p_{d} x_{0}^{d} \\ P\left(x_{1}\right)=p_{0}+p_{1} x_{1}+p_{2} x_{1}^{2}+\cdots+p_{d} x_{1}^{d} \\ \vdots \\ P\left(x_{d}\right)=p_{0}+p_{1} x_{d}+p_{2} x_{d}^{2}+\cdots+p_{d} x_{d}^{d} \end{array} P(x0)=p0+p1x0+p2x02+⋯+pdx0dP(x1)=p0+p1x1+p2x12+⋯+pdx1d⋮P(xd)=p0+p1xd+p2xd2+⋯+pdxdd
上述的表达式也可以写成一个矩阵形式:
[ P ( x 0 ) P ( x 1 ) ⋮ P ( x d ) ] = [ 1 x 0 x 0 2 ⋯ x 0 d 1 x 1 x 1 2 ⋯ x 1 d ⋮ ⋮ ⋮ ⋱ ⋮ 1 x d x d 2 ⋯ x d d ] [ p 0 p 1 ⋮ p d ] \left[\begin{array}{c} P\left(x_{0}\right) \\ P\left(x_{1}\right) \\ \vdots \\ P\left(x_{d}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} & \cdots & x_{0}^{d} \\ 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{d} & x_{d}^{2} & \cdots & x_{d}^{d} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ \vdots \\ p_{d} \end{array}\right] ⎣⎢⎢⎢⎡P(x0)P(x1)⋮P(xd)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡11⋮1x0x1⋮xdx02x12⋮xd2⋯⋯⋱⋯x0dx1d⋮xdd⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡p0p1⋮pd⎦⎥⎥⎥⎤
其中中间的那列就是一个范德蒙德行列式了,秩为1,所以 p 0 , . . . p d p_0,...p_d p0,...pd只有一个解,即多项式的系数确定。因此通过 d + 1 d+1 d+1个点可以唯一确定一个 d d d阶的多项式。

因此,我们可以将一个系数多项式转换为一个点值多项式,然后进行 O ( d ) O(d) O(d)复杂度的两两相乘运算,再将结果的点值多项式恢复回系数多项式就行啦。
但是:这里新的问题就出现了,如果我们采用下方这种矩阵形式来计算点值的话,那么由系数转为点值的复杂度也是 O ( d 2 ) O(d^2) O(d2)的,那不是白忙活了吗。别着急,这时候FFT就有用了。
[ P ( x 0 ) P ( x 1 ) ⋮ P ( x d ) ] = [ 1 x 0 x 0 2 ⋯ x 0 d 1 x 1 x 1 2 ⋯ x 1 d ⋮ ⋮ ⋮ ⋱ ⋮ 1 x d x d 2 ⋯ x d d ] [ p 0 p 1 ⋮ p d ] \left[\begin{array}{c} P\left(x_{0}\right) \\ P\left(x_{1}\right) \\ \vdots \\ P\left(x_{d}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} & \cdots & x_{0}^{d} \\ 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{d} & x_{d}^{2} & \cdots & x_{d}^{d} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ \vdots \\ p_{d} \end{array}\right] ⎣⎢⎢⎢⎡P(x0)P(x1)⋮P(xd)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡11⋮1x0x1⋮xdx02x12⋮xd2⋯⋯⋱⋯x0dx1d⋮xdd⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡p0p1⋮pd⎦⎥⎥⎥⎤
如何加速系数多项式到点值类型多项式的运算?
首先来观察一些多项式:

例如 F ( x ) = x 2 F(x)=x^2 F(x)=x2,对于这样一个对称的多项式来说 F ( − x ) = F ( x ) F(-x)=F(x) F(−x)=F(x),确定了一个点就相当于确定了两个点。因为通过 ( x 0 , F ( x 0 ) ) (x_0,F(x_0)) (x0,F(x0))就可以知道 − x 0 -x_0 −x0所对应的点是 ( − x 0 , F ( x 0 ) ) (-x_0,F(x_0)) (−x0,F(x0))了。同理对于 F ( x 3 ) F(x^3) F(x3)来说 F ( − x ) = − F ( x ) F(-x)=-F(x) F(−x)=−F(x),只要知道了 ( x 0 , F ( x 0 ) ) (x_0,F(x_0)) (x0,F(x0)),就可以知道 − x 0 -x_0 −x0所对应的点是 ( − x 0 , − F ( x 0 ) ) (-x_0,-F(x_0)) (−x0,−F(x0))了。相当于我们只需要找原本的一半的点就可以得到这个多项式了。
基于上面的想法,假如有一个一般形式的多项式:
P ( x ) = 3 x 5 + 2 x 4 + x 3 + 7 x 2 + 5 x + 1 P ( x ) = 2 x 4 + 7 x 2 + 1 + ( 3 x 5 + x 3 + 5 x ) P ( x ) = ( 2 x 4 + 7 x 2 + 1 ) ⏟ P e ( x 2 ) + x ( 3 x 4 + x 2 + 5 ) ⏟ P o ( x 2 ) P ( x ) = P e ( x 2 ) + x P o ( x 2 ) P ( x i ) = P e ( x i 2 ) + x i P o ( x i 2 ) P ( − x i ) = P e ( x i 2 ) − x i P o ( x i 2 ) P(x)=3 x^{5}+2 x^{4}+x^{3}+7 x^{2}+5 x+1\\ P(x)=2x^4+7x^2+1 +(3x^5+x^3+5x) \\ \begin{aligned} P(x)=& \underbrace{\left(2 x^{4}+7 x^{2}+1\right)}_{P_{e}\left(x^{2}\right)}+x \underbrace{\left(3 x^{4}+x^{2}+5\right)}_{P_{o}\left(x^{2}\right)} \\ & P(x)=P_{e}\left(x^{2}\right)+x P_{o}\left(x^{2}\right) \\ & P\left(x_{i}\right)=P_{e}\left(x_{i}^{2}\right)+x_{i} P_{o}\left(x_{i}^{2}\right) \\ & P\left(-x_{i}\right)=P_{e}\left(x_{i}^{2}\right)-x_{i} P_{o}\left(x_{i}^{2}\right) \end{aligned} P(x)=3x5+2x4+x3+7x2+5x+1P(x)=2x4+7x2+1+(3x5+x3+5x)P(x)=Pe(x2)
(2x4+7x2+1)+xPo(x2)
(3x4+x2+5)P(x)=Pe(x2)+xPo(x2)P(xi)=Pe(xi2)+xiPo(xi2)P(−xi)=Pe(xi2)−xiPo(xi2)
可以把 P e P_e Pe和 P o P_o Po分别看做两个两次的多项式 P e ( x ) = 2 x 2 + 7 x + 1 , P o ( x ) = 3 x 2 + x + 5 P_e(x)=2x^2+7x+1,P_o(x)=3x^2+x+5 Pe(x)=2x2+7x+1,Po(x)=3x2+x+5。对于一个点 x i x_i xi来说,我们还需要计算 P e ( x i 2 ) , P o ( x i 2 ) P_e(x_i^2),P_o(x_i^2) Pe(xi2),Po(xi2)就可以得到 P ( x i ) P(x_i) P(xi)以及 P ( − x i ) P(-x_i) P(−xi)的值了。且 P e P_e Pe和 P o P_o Po还可以进一步拆分为奇偶两部分。
假设原本我们对于 P ( x ) P(x) P(x)要求的点是 ± x 1 , ± x 2 , … , ± x n / 2 \pm x_{1}, \pm x_{2}, \ldots, \pm x_{n / 2} ±x1,±x2,…,±xn/2,用这 n n n个点来确定一个 n − 1 n-1 n−1阶的多项式。现在我们变成了求 P e ( x ) , P o ( x ) P_e(x),P_o(x) Pe(x),Po(x)在 x 1 2 , x 2 2 , . . . , x n / 2 2 x_1^2,x_2^2,...,x_{n/2}^2 x12,x22,...,xn/22上面的点值。如果说他们两两之间满足某个 x i 2 = − x j 2 x_i^2=-x^2_j xi2=−xj2的话,那就可以进一步拆分为一半了。那就可以将原来 O ( n 2 ) O(n^2) O(n2)的复杂度降为 O ( n l o g n ) O(n\ logn) O(n logn)。
问题又出现了, x 1 2 , x 2 2 , . . . , x n / 2 2 x_1^2,x_2^2,...,x_{n/2}^2 x12,x22,...,xn/22之间并不满足两两互为相反数的条件呀。而且我们需要这几个数再平方之后仍然是两两之间互为相反数。
所以这里就要引入n次单位根了,不是随机选取 n n n个点,而是采用 [ ω 0 , ω 1 , ω 2 , … , ω n − 1 ] \left[\omega^{0}, \omega^{1}, \omega^{2}, \ldots, \omega^{n-1}\right] [ω0,ω1,ω2,…,ωn−1]这n个点。
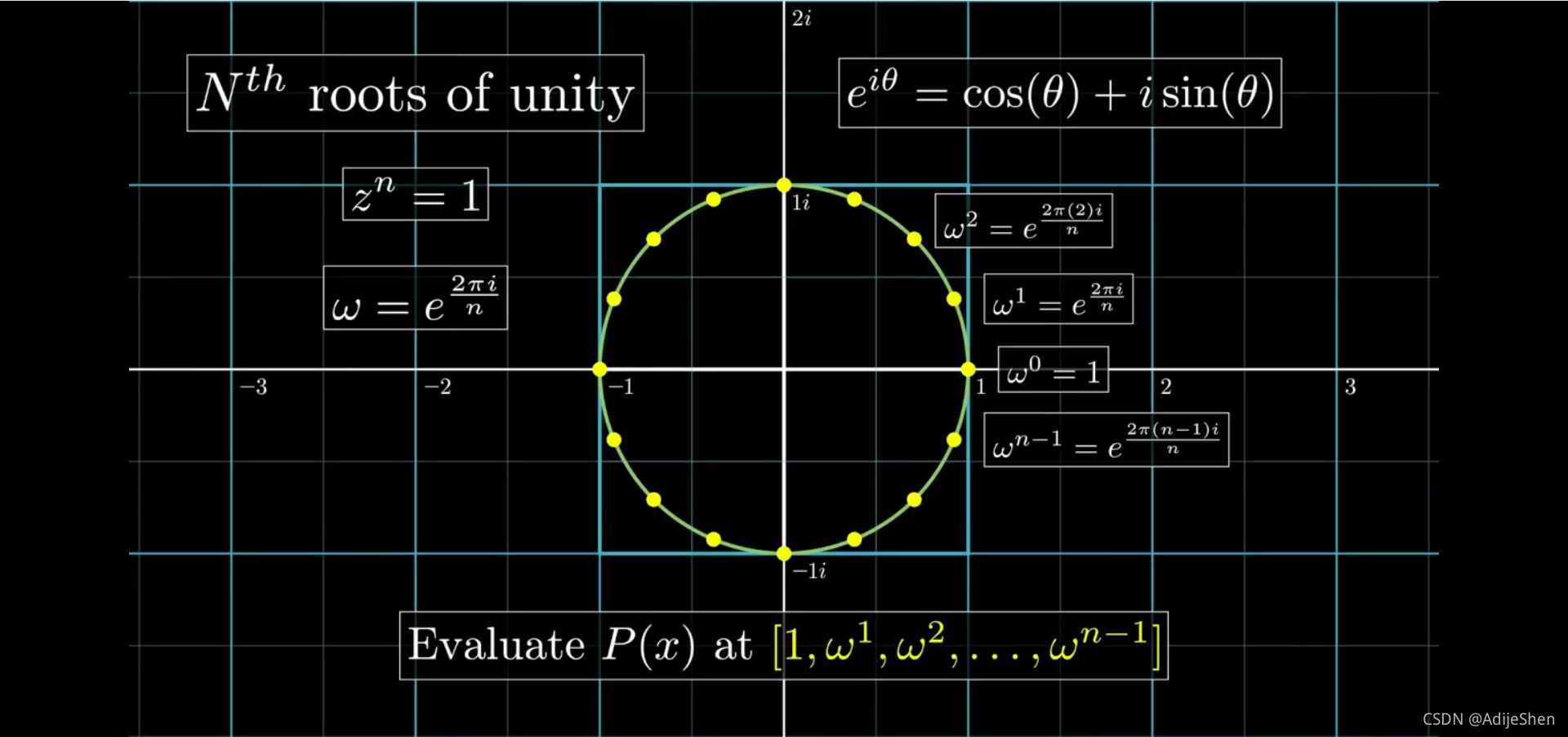
对于 n n n个点 ω 0 , . . . ω n − 1 \omega_0,...\omega_{n-1} ω0,...ωn−1来说,他们满足 − ω i = ω i + n 2 -\omega_i = \omega_{i+{\frac{n}{2}}} −ωi=ωi+2n, ω n + i = ω i \omega_{n+i}=\omega_{i} ωn+i=ωi, ω n − i = ω i ‾ \omega_{n-i}=\overline{\omega_i} ωn−i=ωi。

因此,这样的点平方之后还是满足两两互为相反数的性质。

所以可以看到,可以将一个 n n n个点的求值问题转换为 n / 2 n/2 n/2个的,再转为 n / 4 n/4 n/4个的,从而达到 O ( n log n ) O(n\log n) O(nlogn)的复杂度。
把这部分转换为伪代码的话就是如下这样:

如何做逆运算?即从点值多项式变为系数多项式
对于计算点值来说,
P ( x ) = p 0 + p 1 x + p 2 x 2 + ⋯ + p n − 1 x n − 1 → { ( x 0 , P ( x 0 ) ) , ( x 1 , P ( x 1 ) ) , … , ( x n − 1 , P ( x n − 1 ) ) } P(x)=p_{0}+p_{1} x+p_{2} x^{2}+\cdots+p_{n-1} x^{n-1}\to\left\{\left(x_{0}, P\left(x_{0}\right)\right),\left(x_{1}, P\left(x_{1}\right)\right), \ldots,\left(x_{n-1}, P\left(x_{n-1}\right)\right)\right\} P(x)=p0+p1x+p2x2+⋯+pn−1xn−1→{
(x0,P(x0)),(x1,P(x1)),…,(xn−1,P(xn−1))}
其实运算的是一个矩阵乘法。
[ P ( x 0 ) P ( x 1 ) ⋮ P ( x d ) ] = [ 1 x 0 x 0 2 ⋯ x 0 n − 1 1 x 1 x 1 2 ⋯ x 1 n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n − 1 x n − 1 2 ⋯ x n − 1 n − 1 ] [ p 0 p 1 ⋮ p n − 1 ] \left[\begin{array}{c} P\left(x_{0}\right) \\ P\left(x_{1}\right) \\ \vdots \\ P\left(x_{d}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} & \cdots & x_{0}^{n-1} \\ 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^{2} & \cdots & x_{n-1}^{n-1} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ \vdots \\ p_{n-1} \end{array}\right] ⎣⎢⎢⎢⎡P(x0)P(x1)⋮P(xd)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡11⋮1x0x1⋮xn−1x02x12⋮xn−12⋯⋯⋱⋯x0n−1x1n−1⋮xn−1n−1⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡p0p1⋮pn−1⎦⎥⎥⎥⎤
将点换为 n n n次单位根 ω \omega ω,则这个矩阵就变为了
[ P ( ω 0 ) P ( ω 1 ) P ( ω 2 ) ⋮ P ( ω n − 1 ) ] = [ 1 1 1 ⋯ 1 1 ω ω 2 ⋯ ω n − 1 1 ω 2 ω 4 ⋯ ω 2 ( n − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ω n − 1 ω 2 ( n − 1 ) ⋯ ω ( n − 1 ) ( n − 1 ) ] ⏟ Discrete Fourier Transform (DFT) matrix [ p 0 p 1 p 2 ⋮ p n − 1 ] \left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right]=\underbrace{\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^{2} & \cdots & \omega^{n-1} \\ 1 & \omega^{2} & \omega^{4} & \cdots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)} \end{array}\right]}_{\text {Discrete Fourier Transform (DFT) matrix }}\left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right] ⎣⎢⎢⎢⎢⎢⎡P(ω0)P(ω1)P(ω2)⋮P(ωn−1)⎦⎥⎥⎥⎥⎥⎤=Discrete Fourier Transform (DFT) matrix ⎣⎢⎢⎢⎢⎢⎡111⋮11ωω2⋮ωn−11ω2ω4⋮ω2(n−1)⋯⋯⋯⋱⋯1ωn−1ω2(n−1)⋮ω(n−1)(n−1)⎦⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡p0p1p2⋮pn−1⎦⎥⎥⎥⎥⎥⎤
其中中间的范德蒙德矩阵就成了一个DFT矩阵。
那有了这个正向(从系数到点值)的矩阵变换,求逆向(从点值到系数)也是非常方便的,就是对上面的矩阵求逆:
[ p 0 p 1 p 2 ⋮ p n − 1 ] = [ 1 1 1 ⋯ 1 1 ω ω 2 ⋯ ω n − 1 1 ω 2 ω 4 ⋯ ω 2 ( n − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ω n − 1 ω 2 ( n − 1 ) ⋯ ω ( n − 1 ) ( n − 1 ) ] − 1 [ P ( ω 0 ) P ( ω 1 ) P ( ω 2 ) ⋮ P ( ω n − 1 ) ] \left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right]=\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^{2} & \cdots & \omega^{n-1} \\ 1 & \omega^{2} & \omega^{4} & \cdots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)} \end{array}\right]^{-1}\left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right] ⎣⎢⎢⎢⎢⎢⎡p0p1p2⋮pn−1⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎡111⋮11ωω2⋮ωn−11ω2ω4⋮ω2(n−1)⋯⋯⋯⋱⋯1ωn−1ω2(n−1)⋮ω(n−1)(n−1)⎦⎥⎥⎥⎥⎥⎤−1⎣⎢⎢⎢⎢⎢⎡P(ω0)P(ω1)P(ω2)⋮P(ωn−1)⎦⎥⎥⎥⎥⎥⎤
即:
[ p 0 p 1 p 2 ⋮ p n − 1 ] = 1 n [ 1 1 1 ⋯ 1 1 ω − 1 ω − 2 ⋯ ω − ( n − 1 ) 1 ω − 2 ω − 4 ⋯ ω − 2 ( n − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ω − ( n − 1 ) ω − 2 ( n − 1 ) ⋯ ω − ( n − 1 ) ( n − 1 ) ] [ P ( ω 0 ) P ( ω 1 ) P ( ω 2 ) ⋮ P ( ω n − 1 ) ] \left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right]=\frac{1}{n}\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega^{-1} & \omega^{-2} & \cdots & \omega^{-(n-1)} \\ 1 & \omega^{-2} & \omega^{-4} & \cdots & \omega^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{-(n-1)} & \omega^{-2(n-1)} & \cdots & \omega^{-(n-1)(n-1)} \end{array}\right]\left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right] ⎣⎢⎢⎢⎢⎢⎡p0p1p2⋮pn−1⎦⎥⎥⎥⎥⎥⎤=n1⎣⎢⎢⎢⎢⎢⎡111⋮11ω−1ω−2⋮ω−(n−1)1ω−2ω−4⋮ω−2(n−1)⋯⋯⋯⋱⋯1ω−(n−1)ω−2(n−1)⋮ω−(n−1)(n−1)⎦⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡P(ω0)P(ω1)P(ω2)⋮P(ωn−1)⎦⎥⎥⎥⎥⎥⎤
从上面的事情我们可以知道,DFT是将 ω \omega ω作为点值传入,IDFT其实就是将 1 n ω − 1 \frac{1}{n}\omega^{-1} n1ω−1作为点值传入,FFT其实就是对DFT的快速算法,由此,IFFT的算法也很好得到:

CKKS Encoding
思路
回顾一下FFT的本质,就是用点值的两两相乘来代替多项式系数的乘法。从而达到加速的效果。
而逆FFT,是把原本两两相乘的点值变回一个多项式
这就很有趣了,因为在RLWE类型的同态加密方案里面,明文的空间是一个多项式,操作是多项式加法和多项式乘法。那如果说我把一个向量做IFFT,变成了一个多项式,把这个多项式作为明文,那就完成了向量的两两之间的加法和乘法,也就是SIMD操作。这也是CKKS的Encoding的核心思路。
通过IFFT构造Toy Encode
这段的内容来自openmined,原文有notebook代码,还是非常易懂的。
假设现在有个需求,要把 N N N个复数 z ∈ C N z\in \mathbb{C}^N z∈CN编码到一个复数系数的多项式上: m ( X ) ∈ C [ X ] / X N + 1 m(X)\in\mathbb{C}[X]/X^N+1 m(X)∈C[X]/XN+1。还要做一个解码:从 C [ X ] / X N + 1 → C N \mathbb{C}[X]/X^N+1 \to \mathbb{C}^{N} C[X]/XN+1→CN。
记映射 σ : C [ X ] / X N + 1 → C N \sigma:\mathbb{C}[X]/X^N+1 \to \mathbb{C}^{N} σ:C[X]/XN+1→CN,逆映射 σ − 1 : C N → C [ X ] / X N + 1 \sigma^{-1}:\mathbb{C}^N\to \mathbb{C}[X]/X^N+1 σ−1:CN→C[X]/XN+1。
最简单构造这样的映射的方法就是令 σ \sigma σ为FFT, σ \sigma σ运算就是计算 m ( X ) m(X) m(X)在 N N N次单位根 ω 0 , ω 1 , . . . ω N − 1 \omega^0,\omega^1,...\omega^N-1 ω0,ω1,...ωN−1上面的值。
注意到,我们这里使用的是分圆多项式 C [ X ] / X N + 1 \mathbb{C}[X]/X^N+1 C[X]/XN+1,所以采用之前的 ω N = 1 \omega^N=1 ωN=1的 N N N次单位根 ω \omega ω已经不合适了,这里采用的是 2 N 2N 2N次单位根 ξ \xi ξ,满足 ξ N + 1 = 0 \xi^N+1=0 ξN+1=0,既 ξ N = − 1 → ξ 2 N = 1 \xi^{N}=-1\to\xi^{2N}=1 ξN=−1→ξ2N=1。
这里我是这么理解的,对于FFT来说,他适用的是一个循环卷积,即 Z [ X ] / X N − 1 Z[X]/X^N-1 Z[X]/XN−1上,那么 X N + k = X k X^{N+k}=X^k XN+k=Xk,而RLWE用的是第2N个分圆多项式,即 Z [ X ] / X N + 1 Z[X]/X^N+1 Z[X]/XN+1,是逆循环的,所以这里要找满足 X N + 1 = 0 X^N+1=0 XN+1=0的根 ξ \xi ξ,而不是 X N = 1 X^N=1 XN=1的根 ω \omega ω。
那么新的解码函数 σ \sigma σ就定义为对于一个多项式 m ( X ) = ∑ i = 0 N − 1 a i X i ∈ C [ X ] / ( X N + 1 ) m(X)=\sum_{i=0}^{N-1}a_iX^i\in\mathbb{C}[X]/(X^N+1) m(X)=∑i=0N−1aiXi∈C[X]/(XN+1),生成一个复数向量 m ( ξ ) , m ( ξ 3 ) , . . . , m ( ξ 2 i + 1 ) , . . . m ( ξ 2 N − 1 ) ∈ C N m(\xi),m(\xi^3),...,m(\xi^{2i+1}),...m(\xi^{2N-1})\in \mathbb{C}^N m(ξ),m(ξ3),...,m(ξ2i+1),...m(ξ2N−1)∈CN。
σ − 1 : [ a 0 a 1 a 2 ⋮ a N − 1 ] = [ 1 ξ ξ 2 ⋯ ξ N − 1 1 ξ 3 ξ 6 ⋯ ξ 3 ( N − 1 ) 1 ξ 5 ξ 10 ⋯ ξ 5 ( N − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ξ 2 N − 1 ξ ( 2 N − 1 ) 2 ⋯ ξ ( 2 N − 1 ) ( N − 1 ) ] − 1 [ m ( ξ 1 ) m ( ξ 3 ) m ( ξ 5 ) ⋮ m ( ξ 2 N − 1 ) ] \sigma^{-1}: \left[\begin{array}{c} a_{0} \\ a_{1} \\ a_{2} \\ \vdots \\ a_{N-1} \end{array}\right] =\left[\begin{array}{ccccc} 1 & \xi & \xi^2 & \cdots & \xi^{N-1} \\ 1 & \xi^{3}& \xi^{6} & \cdots & \xi^{3({N-1})} \\ 1 & \xi^{5} & \xi^{10} & \cdots & \xi^{5(N-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \xi^{2N-1} & \xi^{(2N-1)2} & \cdots & \xi^{(2N-1)(N-1)} \end{array}\right]^{-1}\left[\begin{array}{c} m\left(\xi^{1}\right) \\ m\left(\xi^{3}\right) \\ m\left(\xi^{5}\right) \\ \vdots \\ m\left(\xi^{2N-1}\right) \end{array}\right] σ−1:⎣⎢⎢⎢⎢⎢⎡a0a1a2⋮aN−1⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎡111⋮1ξξ3ξ5⋮ξ2N−1ξ2ξ6ξ10⋮ξ(2N−1)2⋯⋯⋯⋱⋯ξN−1ξ3(N−1)ξ5(N−1)⋮ξ(2N−1)(N−1)⎦⎥⎥⎥⎥⎥⎤−1⎣⎢⎢⎢⎢⎢⎡m(ξ1)m(ξ3)m(ξ5)⋮m(ξ2N−1)⎦⎥⎥⎥⎥⎥⎤
σ : [ m ( ξ 1 ) m ( ξ 3 ) m ( ξ 5 ) ⋮ m ( ξ 2 N − 1 ) ] = [ 1 ξ ξ 2 ⋯ ξ N − 1 1 ξ 3 ξ 6 ⋯ ξ 3 ( N − 1 ) 1 ξ 5 ξ 10 ⋯ ξ 5 ( N − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ξ 2 N − 1 ξ ( 2 N − 1 ) 2 ⋯ ξ ( 2 N − 1 ) ( N − 1 ) ] [ a 0 a 1 a 2 ⋮ a N − 1 ] \sigma: \left[\begin{array}{c} m\left(\xi^{1}\right) \\ m\left(\xi^{3}\right) \\ m\left(\xi^{5}\right) \\ \vdots \\ m\left(\xi^{2N-1}\right) \end{array}\right] =\left[\begin{array}{ccccc} 1 & \xi & \xi^2 & \cdots & \xi^{N-1} \\ 1 & \xi^{3}& \xi^{6} & \cdots & \xi^{3({N-1})} \\ 1 & \xi^{5} & \xi^{10} & \cdots & \xi^{5(N-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \xi^{2N-1} & \xi^{(2N-1)2} & \cdots & \xi^{(2N-1)(N-1)} \end{array}\right] \left[\begin{array}{c} a_{0} \\ a_{1} \\ a_{2} \\ \vdots \\ a_{N-1} \end{array}\right] σ:⎣⎢⎢⎢⎢⎢⎡m(ξ1)m(ξ3)m(ξ5)⋮m(ξ2N−1)⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎡111⋮1ξξ3ξ5⋮ξ2N−1ξ2ξ6ξ10⋮ξ(2N−1)2⋯⋯⋯⋱⋯ξN−1ξ3(N−1)ξ5(N−1)⋮ξ(2N−1)(N−1)⎦⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡a0a1a2⋮aN−1⎦⎥⎥⎥⎥⎥⎤
举例
考虑一个 N = 4 N=4 N=4的情况, ξ = e 2 π i 2 N = 2 2 + 2 2 i \xi = e^{\frac{2 \pi i}{2N}}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i ξ=e2N2πi=22+22i。
要进行encode的向量为[1,2,3,4],对这个向量进行 σ − 1 \sigma^{-1} σ−1运算,得到
m 1 ( X ) = 2.5 + 2 2 i X + 0.5 i X 2 + 2 2 i X 3 m_1(X)=2.5+\frac{\sqrt{2}}{2}iX+0.5iX^2+\frac{\sqrt{2}}{2}iX^3 m1(X)=2.5+22iX+0.5iX2+22iX3。
可以把 ξ = 2 2 + 2 2 i , ξ 3 = − 2 2 + 2 2 i , , ξ 5 = − 2 2 − 2 2 i , , ξ 7 = 2 2 − 2 2 i \xi=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i,\xi^3=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i,,\xi^5=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i,,\xi^7=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i ξ=22+22i,ξ3=−22+22i,,ξ5=−22−22i,,ξ7=22−22i带入验算一下,可以得到 m 1 ( ξ ) = 1 , m 1 ( ξ 3 ) = 2 , m 1 ( ξ 5 ) = 3 , m 1 ( ξ 7 ) = 4 m_1(\xi)=1,m_1(\xi^3)=2,m_1(\xi^5)=3,m_1(\xi^7)=4 m1(ξ)=1,m1(ξ3)=2,m1(ξ5)=3,m1(ξ7)=4。
所以对[1,2,3,4]encode得[2.5,0.7i,0.5i,0.7i]。
同样的可以对[1,-2,3,-4]进行encode得到[-0.5,-0.7,-2.5i,0.7]。
即 m 2 ( X ) = − 0.5 + − 2 2 X − 2.5 i X 2 + 2 2 X 3 m_2(X)=-0.5+-\frac{\sqrt{2}}{2}X-2.5iX^2+\frac{\sqrt{2}}{2}X^3 m2(X)=−0.5+−22X−2.5iX2+22X3。
令:
m a d d ( X ) = m 1 ( X ) + m 2 ( X ) m o d X N + 1 = 2 + ( − 2 2 + 2 2 i ) X − 2 i X 2 + ( 2 2 + 2 2 i ) X 3 m_{add}(X)=m_1(X)+ m_2(X)\bmod X^N+1=2+(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)X-2iX^2+(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i)X^3 madd(X)=m1(X)+m2(X)modXN+1=2+(−22+22i)X−2iX2+(22+22i)X3
m m u l ( X ) = m 1 ( X ) ⋅ m 2 ( X ) m o d X N + 1 = − 2.5 + ( − 5 2 2 − 2 2 i ) X − 7.5 i X 2 + ( 5 2 2 − 2 2 i ) X 3 m_{mul}(X)=m_1(X) \cdot m_2(X)\bmod X^N+1=-2.5+(-\frac{5\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)X-7.5iX^2+(\frac{5\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i)X^3 mmul(X)=m1(X)⋅m2(X)modXN+1=−2.5+(−252−22i)X−7.5iX2+(252−22i)X3
可以把执行一次decode,得到:
2,0,6,0: m a d d ( ξ ) = 2 , m a d d ( ξ 3 ) = 0 , m a d d ( ξ 5 ) = 6 , m a d d ( ξ 7 ) = 0 m_{add}(\xi)=2,m_{add}(\xi^3)=0,m_{add}(\xi^5)=6,m_{add}(\xi^7)=0 madd(ξ)=2,madd(ξ3)=0,madd(ξ5)=6,madd(ξ7)=0
1,-4,9,-16: m m u l ( ξ ) = 1 , m m u l ( ξ 3 ) = − 4 , m m u l 5 ( ξ ) = 9 , m m u l 7 ( ξ ) = − 16 m_{mul}(\xi)=1,m_{mul}(\xi^3)=-4,m_{mul^5}(\xi)=9,m_{mul^7}(\xi)=-16 mmul(ξ)=1,mmul(ξ3)=−4,mmul5(ξ)=9,mmul7(ξ)=−16
正好是encode前两个向量的按位加和按位乘。
CKKS的Encode
通过上面的举例可以看到,直接对一个 N N N维向量(实数或复数向量)进行IFFT得到的多项式的系数上面是有虚数的。但我们在RLWE当中,所有的多项式系数都是整数。所以CKKS除了进行IFFT还做了一些其他的变化:
首先,将向量复制一份共轭:
比如向量[1+i,2+2i],变为[1+i,2+2i,2-2i,1-i],对这个变化之后的向量做IFFT就可以得到
m ( X ) = 1.5 + 2 2 X − 0.5 X 2 + 2 X 3 m(X)=1.5+\frac{\sqrt{2}}{2}X -0.5X^2+\sqrt{2}X^3 m(X)=1.5+22X−0.5X2+2X3。
为什么会满足这样的性质?对于第2N个分圆多项式 X N + 1 X^N+1 XN+1来说,其单位根 ξ \xi ξ满足 ξ i = ξ 2 N − i ‾ \xi^i=\overline{\xi^{2N-i}} ξi=ξ2N−i, ξ i = − ξ i + N \xi^i=-\xi^{i+N} ξi=−ξi+N的性质。所以对于 R = Z [ X ] / X N + 1 \mathcal{R}=Z[X]/X^N+1 R=Z[X]/XN+1, m ( X ) ∈ R m(X)\in \mathcal{R} m(X)∈R来说, m ( ξ i ) = m ( ξ 2 N − i ‾ ) = m ( ξ 2 N − i ) ‾ m(\xi^i)=m(\overline{\xi^{2N-i}})=\overline{m(\xi^{2N-i})} m(ξi)=m(ξ2N−i)=m(ξ2N−i)。
那么反向的来说只要在令向量的 ξ i \xi^i ξi对应的位置是 ξ 2 N − i \xi^{2N-i} ξ2N−i对应的位置的共轭,那么经过IFFT得到的多项式系数就会在实数域内。
因为要复制一份共轭的关系,也就是对于 N N N个系数来说,我们有效利用的只有 N / 2 N/2 N/2,所以CKKS的encoding中的slot是 N / 2 N/2 N/2。
前面我们已经定义了 σ , σ − 1 \sigma,\sigma^{-1} σ,σ−1操作,分别对应IFFT和FFT,这里再定义 π , π − 1 \pi,\pi^{-1} π,π−1操作。 π − 1 \pi^{-1} π−1操作将 C N / 2 \mathbb{C}^{N/2} CN/2的复数向量复制一份共轭,CKKSpaper里面把这种共轭向量空间称作 H \mathbb{H} H。 π \pi π定义为从 H \mathbb{H} H到 C N / 2 \mathbb{C}^{N/2} CN/2的一个投影(也就是把后面一半扔掉)。
如何从实数多项式到整数多项式?
现在 m ( X ) m(X) m(X)的系数都是实数了,但还不是我们想要的有限域内的整数,所以CKKS的处理方法是将系数扩大再取整。
比如取扩张倍数 Δ = 2 10 = 1024 \Delta=2^{10}=1024 Δ=210=1024,
对于一个向量[1.23+i,2.14+2i]来说,首先我们复制一份共轭( π − 1 \pi^{-1} π−1),得到[1.23+i,2.14+2i,2.14-2i,1.23-i]。然后对其扩张1024倍并执行 σ − 1 \sigma^{-1} σ−1得到 1725.5 + 765.9578 X − 511.999 X 2 + 1415.274 X 3 1725.5+765.9578X-511.999X^2+1415.274X^3 1725.5+765.9578X−511.999X2+1415.274X3,对其进行取整,使得它落在 R \mathcal{R} R上: 1725 + 766 X − 512 X 2 + 1415 X 3 1725+766X-512X^2+1415X^3 1725+766X−512X2+1415X3。就得到了encode之后的多项式。
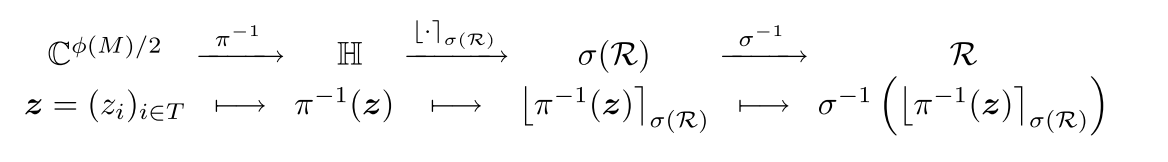
可以和CKKS文章里面的encode方法对应上了。首先是 π − 1 \pi^{-1} π−1复制一份共轭,然后是 σ ( R ) \sigma(R) σ(R)这里我理解成扩张再取整,最后通过一个 σ − 1 \sigma^{-1} σ−1修改后的IFFT得到最终的多项式。
现在可以执行decode了:
decode相对简单, z = π ∘ σ ( Δ − 1 ⋅ m ) z=\pi \circ \sigma\left(\Delta^{-1} \cdot m\right) z=π∘σ(Δ−1⋅m)
对于多项式 1725 + 766 X − 512 X 2 + 1415 X 3 1725+766X-512X^2+1415X^3 1725+766X−512X2+1415X3
先把他执行 σ \sigma σ得到
[1259.72373798+1023.83592874j, 2190.27626202+2047.83592874j, 2190.27626202-2047.83592874j, 1259.72373798-1023.83592874j],
然后除以 Δ = 1024 \Delta=1024 Δ=1024得到[1.23019896+0.99983977j, 2.13894166+1.99983977j, 2.13894166-1.99983977j, 1.23019896-0.99983977j],
再进行 π \pi π得到[1.23019896+0.99983977j, 2.13894166+1.99983977j]。
就是和原始输入向量近似的一个向量啦。