概述
400多年前,西班牙文学大师塞万提斯在其巨作《唐吉珂德》中提出了一个被投资界奉为经典的思想:“智者不会把所有的鸡蛋放在同一个蓝子里”。
那么如何分散投资才能实现最大程度地获取收益而最小程度的承担风险呢?资产配置主要就是解决这个问题。
资产配置是将财富分散到各种不同的资产中,目的是为了在未来某个时点达成某个收益目标,通过合理的配置,能够在达成收益目标的过程中,将财富的波动程度控制在个人可以接受的范围之内,并有很大的几率能够达成目标。显然,在资产未来的价格充满不确定性的前提下,资产配置有其必要性。
投资组合的收益率与风险
在拓展到N种风险资产之前,先来看两种风险资产的情形。假设现在市场有资产A和B,其随机收益率分别为RA和RB,若投资人将其财富的一部分投入到资产A,剩下的投入到资产B,投资比例分别为WA和WB,且WA+WB=1,如果投资人初期资本为W0,则在资产A上的收益为W0WARA,在资产B上的收益为WOWBRB,总的收益为W0WARA+W0WBRB。
知道初始资本、收益即可求得投资组合的收益率RP
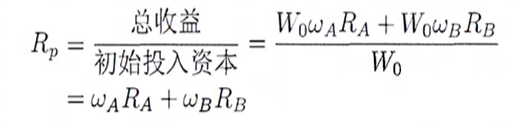
两个资产组成的投资组合的方差为:
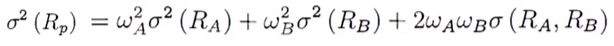
标准差:
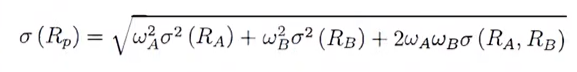
其中
投资组合理论
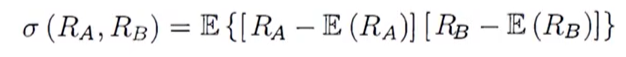
其中
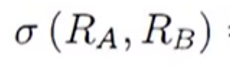
为资产A与资产B的协方差
从公式可以看了,如果资产A与资产B收益率变化趋势是一致的(比如资产A的收益率高于期望值时,资产B的收益率也高于期望值),则其协方差为正; 反之,若变化趋势相反,由协方差为负。协方差常常用来判断两个变量之间的相关性,不过由于协方差会受比例影响(比如把RA和RB同时扩大10倍,协方差会放大100倍),因此统计学家引入相关系数来刻画两个变量之间的相关性。资产A和资产B收益率之间的相关系数为:

风险分散
概述
当投资比例维持不变时,两资产的相关系数越高,风险越大,这个结果很符合直觉:若两资产收益率同向变动,当收益大于其期望值的情境发生时,两资产的收益均大于各自的期望值,反之均小于各自的期望值,总的收益变动比较剧烈; 若两资产的收益率反向变动,两资产的收益一个会高于期望值,一个会低于期望值,一高一低会使总的收益变动幅度减小,达到降低风险的作用。
分散化投资可以降低风险。通常,我们认为证券投资的风险由两部分组成:系统性风险和非系统风险。
非系统性风险
又被称为可分散风险,是指只对特定行业或特定公司的证券产生影响的风险,比如油价的调整会影响到石油行业的公司,也会影响到运输行业的个股股价,但是也有很多股票可能不受影响。
不同的公司在同一段时间内所遭受的的非系统性风险可能不同,比如A公司可能由于研发活动成功而股价大增,B公司可能由于丢失订单而股价大减,若共同持有两只股票,损益会相互抵消,从而降低收益率的波动并减小风险,因此非系统性风险是可以通过分散化投资消除的。
系统性风险
是对整个股票市场的普遍产生不利影响的风险,该类风险的来源多是政治环境、整体经济等关系全局的因素。系统性风险是无法通过分散化投资降低的,比如2008年金融海啸发生时,所有的股票价格都下跌,投资人无法通过分散化投资来获得稳定的收益。
系统性风险是无法通过分散投资进行风险消除。
利率风险和汇率风险都属于系统性风险。
方差模型-马科维茨(Markowitz)均值
概述
证券及其它风险资产的投资首先需要解决的是两个核心问题:即预期收益与风险。 那么如何测定组合投资的风险与收益和如何平衡这两项指标进行资产分配是市场投资者迫切需要解决的问题。正是在这样的背景下,在50年代和60年代初,马科维茨理论应运而生。
假设条件
该理论依据以下几个假设:
1、投资者在考虑每一次投资选择时,其依据是某一持仓时间内的证券收益的概率分布。
2、投资者是根据证券的期望收益率估测证券组合的风险。
3、投资者的决定仅仅是依据证券的风险和收益。
4、在一定的风险水平上,投资者期望收益最大;相对应的是在一定的收益水平上,投资者希望风险最小。
根据以上假设,马可维兹确立了证券组合预期收益、风险的计算方法和有效边界理论,建立了资产优化配置的均值-方差模型:
目标函数:minб2(rp)=∑∑xixjCov(ri,rj)
rp= ∑xiri
限制条件: 1=∑Xi (允许卖空)
或 1=∑Xi xi>≥0(不允许卖空)
其中rp为组合收益, ri为第i只股票的收益,xi、 xj为证券 i、j的投资比例,б2(rp)为组合投资方差(组合总风险),Cov (ri 、rj ) 为两个证券之间的协方差。该模型为现代证券投资理论奠定了基础。上式表明,在限制条件下求解Xi 证券收益率使组合风险б2(rp )最小,可通过朗格朗日目标函数求得。其经济学意义是,投资者可预先确定一个期望收益,通过上式可确定投资者在每个投资项目(如股票)上的投资比例(项目资金分配),使其总投资风险最小。不同的期望收益就有不同的最小方差组合,这就构成了最小方差集合。
经济金融领域分析个人行为时往往会谈到效用,在研究投资人资产配置行为时也不例外。
假定现在投资人初始的财富为W,在N种资产上的投资比重分别为W1,W2,….WN,未来收益为Rp,则投资人的未来财富水平W=Wo(1+Rp),由于Rp是随机变量,未来财富水平W也是一个随机变量。如果投资人的效用水平仅与财富状况有关,则效用水平U(Rp)也是随机变量,其期望值为E[U(Rp)]。通常在经济金融领域,我们认为个人决策的出发点是为了最大化效用(或期望效用),投资决策过程就可以精简成以下公式:
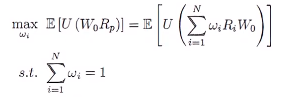
现在进一步假定,投资人的效用函数是常见的凹函数,则投资人的决策问题公式可以简化为:
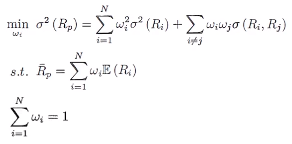
其中RP为投资人的投资目标,即投资人期待投资组合的期望值达到RP,公式说明投资人资产分配的原则是在达成投资目标RP的前提下,要将资产组合的风险最小化,决策变量为Wi=1,…..,N,整个数学形式是二次规划问题,可以用拉格朗日方法求解。
因此,当达到最优解时,风险水平δ(Rp)是投资目标Rp的二次函数形式。如果用图形表示投资目标与最优解下标准差的关系,如下图所示:
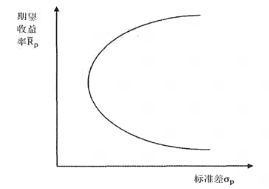
图中的曲线为最小方差前缘,即在特定的投资目标下能够令投资组合收益率方差(标准差)最小的资产配置比例。该线的上半段曲线被称为效率前缘,效率前缘上的资产配比既可以在特定的投资目标Rp下达到风险最小,又可以在特定的风险水平下达到期望收益率最大。
投资组合标准差代码实现
Markowitz模型代码实现
import numpy as np
from cvxopt import matrix,solvers
def Markowitz(returns,cov,target_return):
p=matrix(cov)
q=matrix((np.zero((len(returns))))
G=matrix((np.zero((len(returns))))
h=matrix([0])
A=matrix(returns)
b=matrix([target_return])
result=solvers.qp(P,q,G,h,A,b)
weight=np.array(result[‘x'])[:,0]
return weight