介绍
- 卡尔曼滤波(Kalman filter)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。它的提出者,鲁道夫.E.卡尔曼,在一次访问NASA埃姆斯研究中心时,发现这种方法能帮助解决阿波罗计划的轨道预测问题,后来NASA在阿波罗飞船的导航系统中确实也用到了这个滤波器。
- 只要是存在不确定信息的动态系统,卡尔曼滤波就可以对系统下一个状态做出推测。即便有噪声信息干扰,卡尔曼滤波通常也能很好工作。因此卡尔曼滤波非常适合不断变化的系统,它的优点还有内存占用较小(只需保留前一个状态)、速度快,是实时问题和嵌入式系统的理想选择。
原理
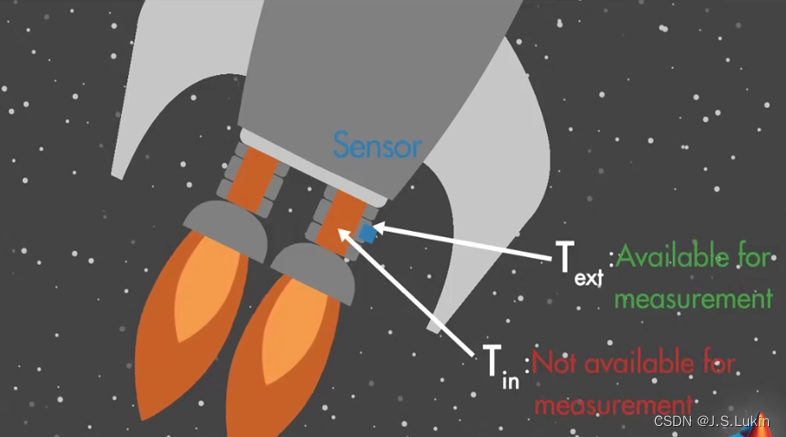
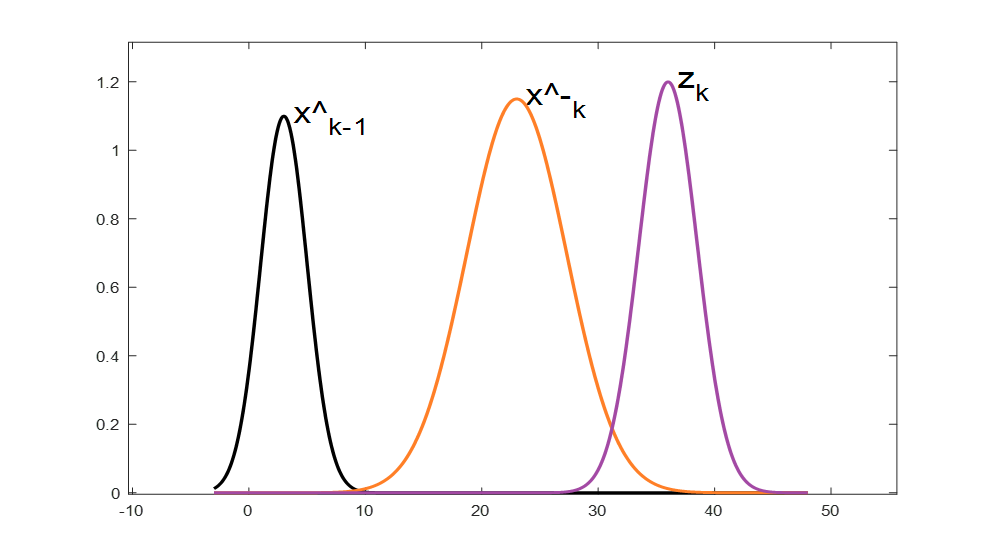
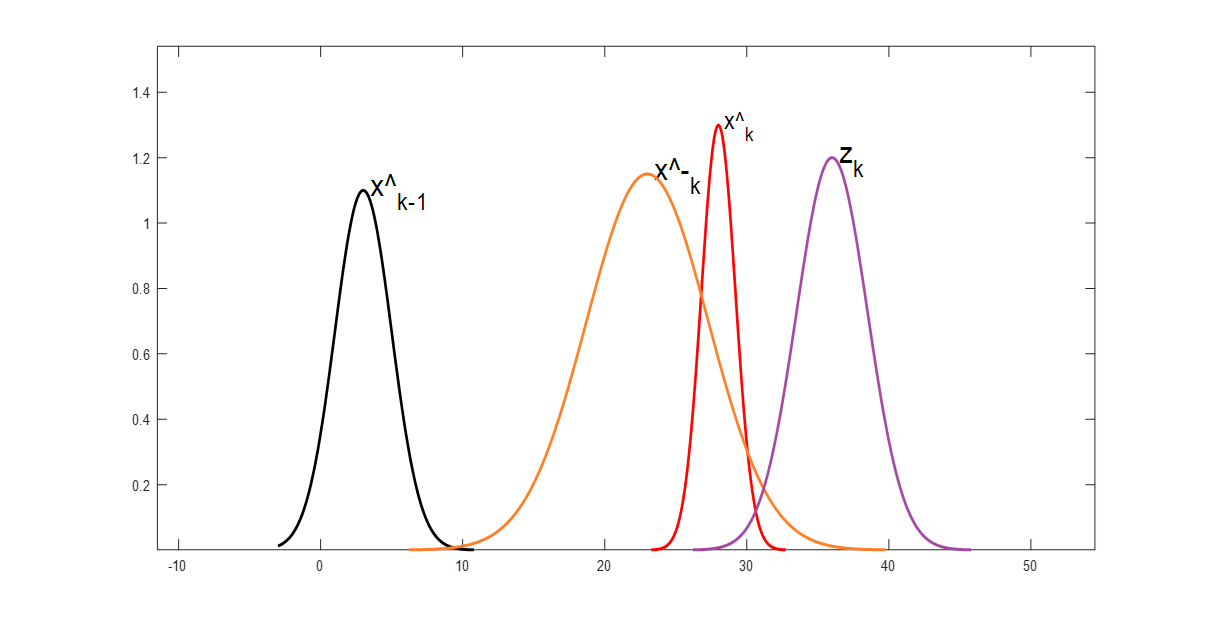
状态方程: x k = A x k − 1 + B u k + w k x_k=Ax_{k-1}+Bu_k+w_k xk=Axk−1+Buk+wk
观测方程: z k = H x k + v k z_k=Hx_k+v_k zk=Hxk+vk
过程噪声: w k ∈ N ( 0 ; Q k ) w_k \in N(0;Q_k) wk∈N(0;Qk)
观测噪声(高斯白噪声): v k ∈ N ( 0 ; R k ) v_k \in N(0;R_k) vk∈N(0;Rk)

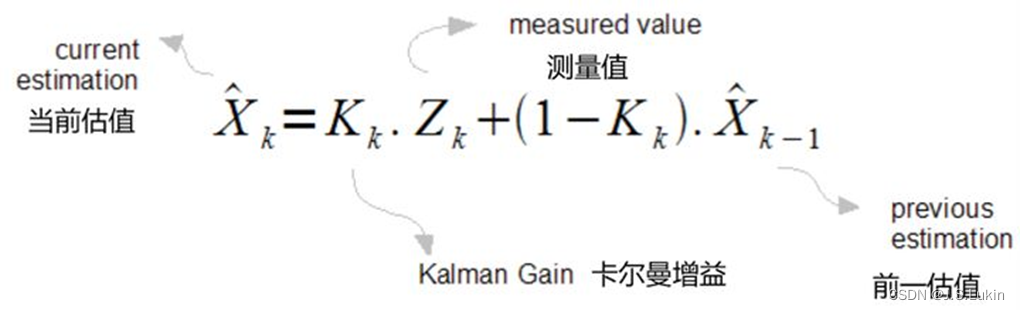
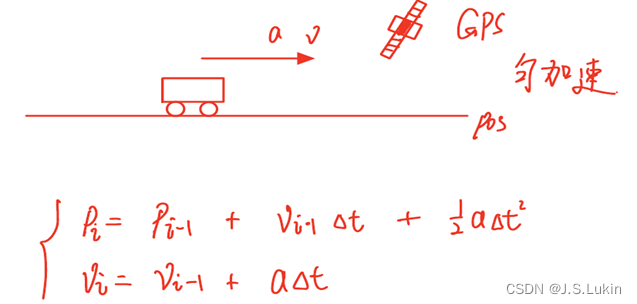
假设小车以a为加速度,速度为v直线前进,某时刻小车的位置与速度为:
P i = P i − 1 + v i Δ t + 1 2 a Δ t 2 v i = v i − 1 + a Δ t P_i = P_{i-1} + v_i \Delta t + \frac{1}{2}a\Delta t^2 \\ v_i = v_{i-1}+a \Delta t Pi=Pi−1+viΔt+21aΔt2vi=vi−1+aΔt
1.二维状态:
x t = [ P v ] x_t=\left[ \begin{matrix} P \\ v \end{matrix} \right] xt=[Pv]
[ P v ] = [ 1 Δ t 0 1 ] [ P i − 1 v i − 1 ] + [ Δ t 2 2 Δ t ] a i \left[ \begin{matrix} P \\ v \end{matrix} \right]=\left[ \begin{matrix} 1 & \Delta t\\ 0 & 1 \end{matrix} \right]\left[ \begin{matrix} P_{i-1}\\ v_{i-1} \end{matrix} \right]+\left[ \begin{matrix} \frac{\Delta t^2}{2} \\ \Delta t \end{matrix} \right]a_i [Pv]=[10Δt1][Pi−1vi−1]+[2Δt2Δt]ai
即先验估计:
x ^ t − = F ⋅ x ^ t − 1 + B u t \hat x_t^-=F \cdot \hat x_{t-1} + Bu_t x^t−=F⋅x^t−1+But
2.先验协方差
P t − = F P t − 1 F T + Q P_t^-=FP_{t-1}F_T +Q Pt−=FPt−1FT+Q
C o v ( x ^ t − , x ^ t − ) = C o v ( F x ^ t − 1 + B u t , F x ^ t − 1 + B u t ) = C o v ( F x ^ t − 1 , F x ^ t − 1 ) = F C o v ( x ^ t − 1 , x ^ t − 1 ) F T + C o v ( w t , w t ) Cov(\hat x_t^-,\hat x_t^-)=Cov(F\hat x_{t-1}+Bu_t,F\hat x_{t-1}+Bu_t)\\ =Cov(F\hat x_{t-1},F\hat x_{t-1})\\=FCov(\hat x_{t-1},\hat x_{t-1})F^T+Cov(w_t,w_t) Cov(x^t−,x^t−)=Cov(Fx^t−1+But,Fx^t−1+But)=Cov(Fx^t−1,Fx^t−1)=FCov(x^t−1,x^t−1)FT+Cov(wt,wt)
其中 C o v ( w t , w t ) Cov(w_t,w_t) Cov(wt,wt)即为 Q Q Q,且有以下定义:
C o v ( x , x ) = v a r ( x ) C o v ( A x , A x ) = A C o v ( x , x ) A T C o v ( A x + b , A x + b ) = C o v ( A x , A x ) \begin{aligned} &\boxed{Cov(x,x)=var(x)}\\ &\boxed{Cov(Ax,Ax)=ACov(x,x)A^T}\\ & \boxed{Cov(Ax+b,Ax+b)=Cov(Ax,Ax)}\\ \end{aligned} Cov(x,x)=var(x)Cov(Ax,Ax)=ACov(x,x)ATCov(Ax+b,Ax+b)=Cov(Ax,Ax)
3.卡尔曼增益
K t = P t − H T H P t − + R P t − P t − + R = P t − 1 + Q P t − 1 + Q + R K_t =\frac{P_t^-H^T}{HP_t^-+R}\\ \frac{P_t^-}{P_t^-+R}=\frac{P_{t-1}+Q}{P_{t-1}+Q+R} Kt=HPt−+RPt−HTPt−+RPt−=Pt−1+Q+RPt−1+Q
4.后验估计
x ^ t = x ^ t − + K t ( Z t − H x ^ t − ) \hat x_t=\hat x_t^- + K_t(Z_t-H\hat x_t^-) x^t=x^t−+Kt(Zt−Hx^t−)
即:估计值+权重*(观测值)
其中:
K t = P t − 1 + Q P t − 1 + Q + R K_t=\frac{P_{t-1}+Q}{P_{t-1}+Q+R} Kt=Pt−1+Q+RPt−1+Q
增大Q或降低R即可使得 K t K_t Kt减小,反之可以增大。
5.后验估计协方差
P t = ( I − k t H ) P t − P_t = (I-k_tH)P_t^- Pt=(I−ktH)Pt−
应用
- 扩展卡尔曼滤波(EKF)利用线性化技巧将非线性问题转化为一个近似的线性滤波问题。利用了泰勒级数得到一个近似的线性化模型。
- 无迹卡尔曼滤波(UKF)采用卡尔曼线性滤波框架,对于一步预测方程,使用无迹变换UT来处理均值和协方差的非线性传递问题。没有把高阶项忽略,因此有较高的计算精度。
Matlab代码仿真
具体应用以及原理可以参考《卡尔曼滤波原理及应用------matlab仿真》
% 模拟要求汽车在一维空间的加速和减速过程
% 控制变量u是汽车的加速度
% 状态变量x=[p,v],x^hat=[v,a]
% w为控制变量的随机扰动,v为测量的随机扰动
% Q为w的方差,R为v的方差,假设w与v相互独立
clear
dt = 0.1; % 采样间隔
N = 100; % 仿真数
Q = diag([0,0.05]); R = 1;
A = [1,dt;0,1];
B = [0;dt];
C = [1,0];
P = Q;
I = eye(2);
x0 = [0.2;0]; % 初始位置和速度
xh0 = [0;0]; % x0的估计
u = ones(1,N); % 加速度恒定
w = sqrt(Q)*randn(2,N); % 控制变量的误差2*N
v = sqrt(R)*randn(1,N); % 测量误差1*N
ye_list = zeros(size(u)); % 估计值
yv_list = zeros(size(u)); % 测量值
y_list = zeros(size(u)); % 实际值
cov_list = zeros(size(u)); % 测量方差
for i = 1:numel(u)
xreal = A*x0 + B*u(i); % 真实的状态变量
yreal = C*x0; % 真实的测量
x1 = xreal + w(:,i); % 含噪声的状态变量
yv = yreal + v(i); % 含噪声的测量
xfe = A*xh0 + B*u(i); % 先验的状态变量
Pfe = A*P*A'+ Q; % 先验的状态变量协方差
K = Pfe*C'/(C*Pfe*C'+R); % 卡尔曼最优增益
xh1 = xfe + K*(yv-C*xfe); % 当前的状态估计
ye = C*xh1;
P = (I-K*C)*Pfe;
x0 = x1;xh0 = xh1;
y_list(i) = yreal;
yv_list(i) = yv;
ye_list(i) = ye;
cov_list(i) = C*P*C';
end
ax = (1:N).*dt;
figure(1);
subplot(2,2,1);plot(ax,y_list,ax,yv_list,ax,ye_list)
legend('实际','测量','估计','Location','best')
title('汽车的位移');ylabel('位移/m');xlabel('时间/s')
subplot(2,2,2);plot(ax,yv_list-y_list,ax,ye_list-y_list)
legend('测量','估计','Location','best');title('汽车的位移误差')
ylabel('位移/m');xlabel('时间/s');
subplot(2,2,[3,4]);plot(ax,cov_list);
legend('测量方差','Location','best');title('测量方差');
ylabel('方差/m^2');xlabel('时间/s');
