基于最小二乘法的直线拟合原理及C++实现

“ 在数据分析的时候，需要尽可能地排除噪声干扰，以便分析出数据的本质规律。排除噪声干扰的常用手段之一是数据拟合，以直线、抛物线、多次曲线等为数据模型，对数据进行拟合。”

本文我们主要讲基于最小二乘法的直线拟合原理，并在此基础上，介绍结合最小二乘法和RANSAC算法的直线拟合算法。

—

基于最小二乘法的直线拟合原理

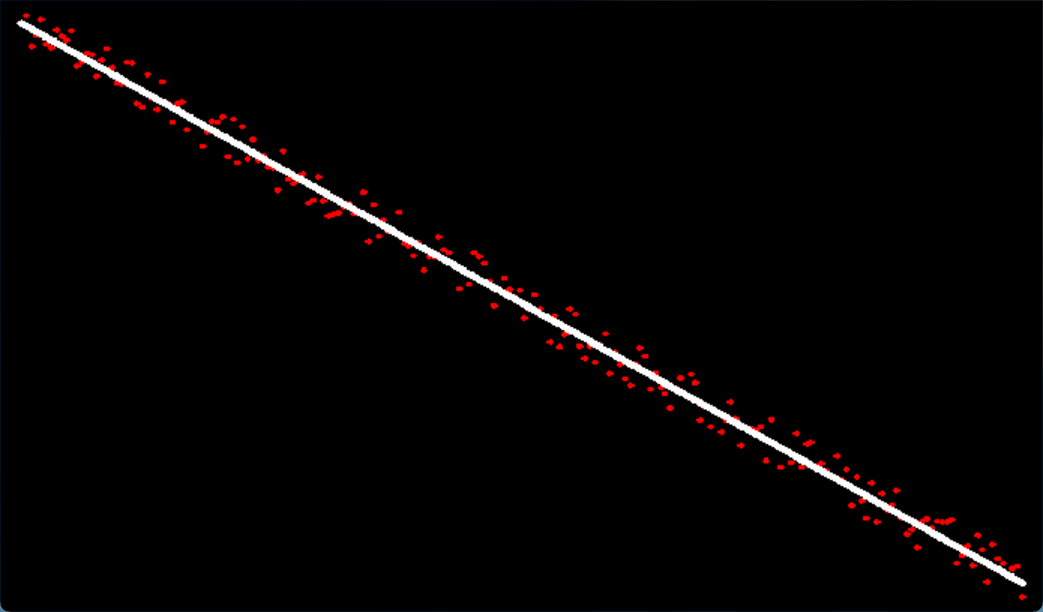
最小二乘法直线拟合的核心思想是：以所有样本值与其对应模型值的平方差和作为目标函数，当目标函数值取得最小值时，认为模型就是所有样本的拟合。

我们知道，当导数为0的时候函数取得极值，所以可通过求目标函数对各参数的偏导数并令偏导数为0来求解各参数。在偏导数为0的情况下求得的各参数则构成了最小二乘法的解。

下面我们来推导一下最小二乘法直线拟合的计算公式。

假设有n个点(x_i, y_i)（0≤i<n），并假设它们的拟合直线为Y=ax+b，那么对于每个x_i，它的拟合值为Y_i=ax_i+b。于是目标函数为：

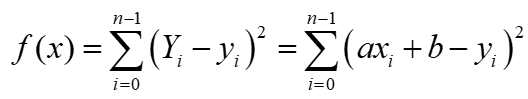
我们的目标是：求当f(x)取得最小值时的a、b参数。于是分别求f(x)对于a、b的偏导数：

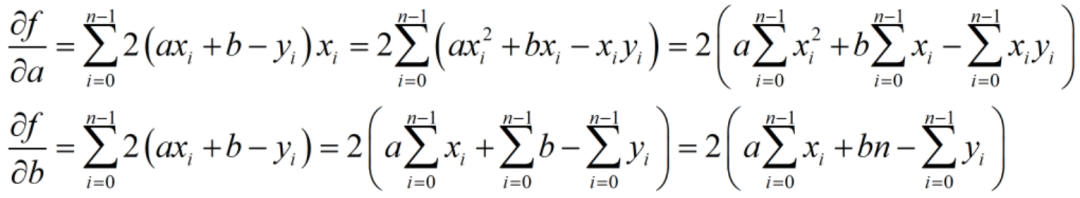
令以上偏导数为0，得到一个二元一次方程组：

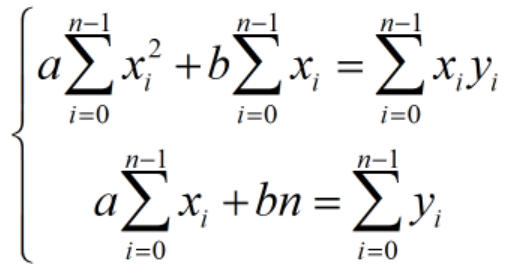
记：

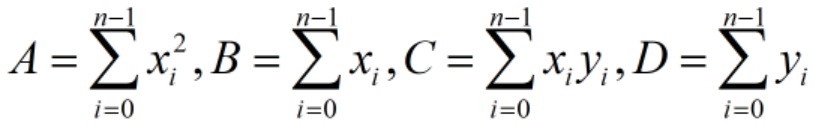
于是有：

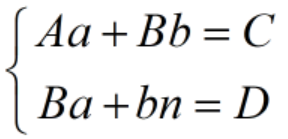
解以上方程组得到a、b，就是我们要求的直线拟合参数：

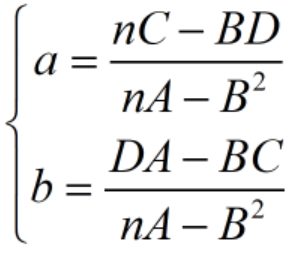
代码实现：

//y=ax+b
void lineplofit(vector<Point2f>& points_list, int points_num, float* a, float* b)
{
    float sum_x2 = 0.0;
    float sum_y = 0.0;
    float sum_x = 0.0;
    float sum_xy = 0.0;


    int num = points_num;


    int i;
    for (i = 0; i < num; ++i)
    {
        sum_x2 += points_list[i].x * points_list[i].x;
        sum_y += points_list[i].y;
        sum_x += points_list[i].x;
        sum_xy += points_list[i].x * points_list[i].y;
    }


    float tmp = num * sum_x2 - sum_x * sum_x;
    if (abs(tmp) > 0.000001f)
    {
        *a = (num * sum_xy - sum_x * sum_y) / tmp;
        *b = (sum_x2 * sum_y - sum_x * sum_xy) / tmp;
    }
    else
    {
        *a = 0;
        *b = 0;
    }
}

—

基于最小二乘法与RANSAC算法的直线拟合原理

上一章节介绍的最小二乘直线拟合算法中，所有样本点都参与计算。但在实际应用过程中因为噪声的存在，往往有个别样本点距离其它大部分点比较远，通常称这些点为离群点，如果离群点也参与直线拟合运算会导致拟合结果出现较大误差。如下图所示：

像以上情况，需要把离群点剔除之后再进行直线拟合，否则会出现较大误差，而RANSAC算法就是这样一种用于剔除离群样本点的经典算法。

介绍RANSAC算法之前，首先讲下内点和外点的含义：与模型距离小于设定阈值的样本点称为内点，反之与模型距离大于等于设定阈值的样本点称为外点（外点也即上文所说的离群点）。举个例子说：假如设定阈值为5，那么若一点到直线的距离为2，因为2小于5所以该点为内点，但若一点到直线的距离为8，因为8大于5所以该点为外点。

下面介绍RANSAC的流程和原理，该算法是一个重复多次循环的过程，在多次循环过程中记录内点数最多的内点集合，最后使用该内点数最多的内点集合来估算拟合模型。

假设历史记录的最多内点集合为MaxInline，且其内点数为MaxM。

1. 首先根据需要设定一个目标模型，如果是直线拟合则模型为y=ax+b，如果是二次曲线拟合则模型为y=ax²+bx+c，如果是仿射变换拟合则模型为2*3的仿射变换矩阵......

2. 从所有样本点中随机选择计算模型参数需要的“最少个数”样本点，假设这个“最少个数”为n，不同的模型对应的n值不一样，如果是直线拟合则n=2，如果是二次曲线拟合则n=3，如果是仿射变换拟合则n=3......

3. 使用上一步随机选取的n个样本点计算模型参数，如果是直线拟合则求a、b，如果是二次曲线拟合则求a、b、c，如果是仿射变换拟合则求2*3矩阵的6个参数......

4. 对每个点，计算其到模型的距离，并判断距离如果小于阈值则该点为内点并将其加入内点集合Inline，否则加入外点集合。同时将Inline的点数m与历史记录的最多内点数MaxM进行比较，如果m>MaxM，则执行MaxM=m且MaxInline=Inline。

5. 判断MaxM是否超过总样本数的一定比例（比如80%），或循环次数是否达到设定的最大循环数。如果MaxM未超过总样本数一定比例且循环次数未达到最大循环数，则跳回以上第2步重新开始往下执行，否则停止循环。

6. 判断是否满足MaxM≥n，如果满足则使用MaxInline集合内的点来估算拟合模型，否则认为RANSAC算法失败。

以上步骤中，需要计算样本点到模型的距离，对于不同的模型其距离计算方法是不一样的。如果是直线模型，则直接计算点(x₀,y₀)到直线y=ax+b的垂直距离即可：

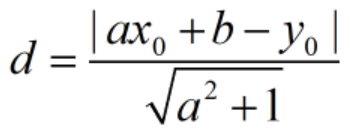
判断内点的距离阈值需要设定一个合适的值，才能有较好的剔除离群点效果，因此可以多次尝试不同的阈值，本文根据最小距离MinD到最大距离MaxD的比例差距，把距离阈值的设定转换为0~1的比例值α设定，减小了设定范围，因此可以更容易找到合适的阈值：

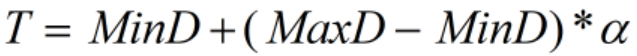
代码实现：

#define RANSAC_K 2


//获取0~n-1范围内的num个随机数
static void GetRansacRandomNum(int n, int num, int p[])
{
    int i = 0, j;


    int r = rand() % n;
    p[0] = r;
    i++;


    while (1)
    {
        int status = 1;
        r = rand() % n;


        for (j = 0; j < i; j++)
        {
            if (p[j] == r)
            {
                status = 0;
                break;
            }
        }


        if (status == 1)
        {
            p[i] = r;
            i++;
        }


        if (i == num)
            break;
    }
}


void RansacPolyfitLine(vector<Point2f> p, int iter_num, float alpha, float* a, float* b)
{
    int r_idx[RANSAC_K];


    vector<Point2f> pick_p;


    srand((unsigned)time(NULL));


    int max_inline_num = 0;


    vector<Point2f> inline_p;
    vector<Point2f> max_inline_p;
    vector<float> d_list;


    int n = p.size();


    for (int i = 0; i < iter_num; i++)   //总共迭代iter_num次
    {
        GetRansacRandomNum(n, RANSAC_K, r_idx);  //生成RANSAC_K个不重复的0~n-1的随机数


        pick_p.clear();
        //随机选择2个点
        for (int j = 0; j < RANSAC_K; j++)
        {       
            pick_p.push_back(p[r_idx[j]]);
        }


        float aa = 0, bb = 0;
        //使用以上随机选择的两个点来计算一条直线
        lineplofit(pick_p, RANSAC_K, &aa, &bb);


        float mind = 99999999.9f;
        float maxd = -99999999.9f;
        d_list.clear();
        //计算所有点到以上计算直线的距离，并记录最大最小距离
        for (int j = 0; j < n; j++)
        {
            float d = abs(aa * p[j].x - p[j].y + bb) / sqrtf(aa * aa + 1.0f);
            d_list.push_back(d);
            mind = MIN(mind, d);
            maxd = MAX(maxd, d);
        }
        //根据0~1的α值和最大最小距离计算阈值
        float threld = mind + (maxd - mind) * alpha;


        inline_p.clear();
        for (int j = 0; j < n; j++)
        {
            //判断如果点距离小于阈值则将该点加入内点集合
            if (d_list[j] < threld)
            {               
                inline_p.push_back(p[j]);                          
            }
        }
        //判断如果以上内点集合的点数大于历史最大内点数，则替换历史最大内点数集合
        if (max_inline_num < inline_p.size())
        {
            max_inline_num = inline_p.size();
            max_inline_p.swap(inline_p);
        }
    }
    //判断如果历史最大内点数大于等于2，则使用历史最大内点数集合来计算直线
    if (max_inline_num >= RANSAC_K)
    {
        lineplofit(max_inline_p, max_inline_p.size(), a, b);
    }
    else  //否则RANSAC算法失败
    {
        *a = 0;
        *b = 0;
    }


}

—

直线拟合结果

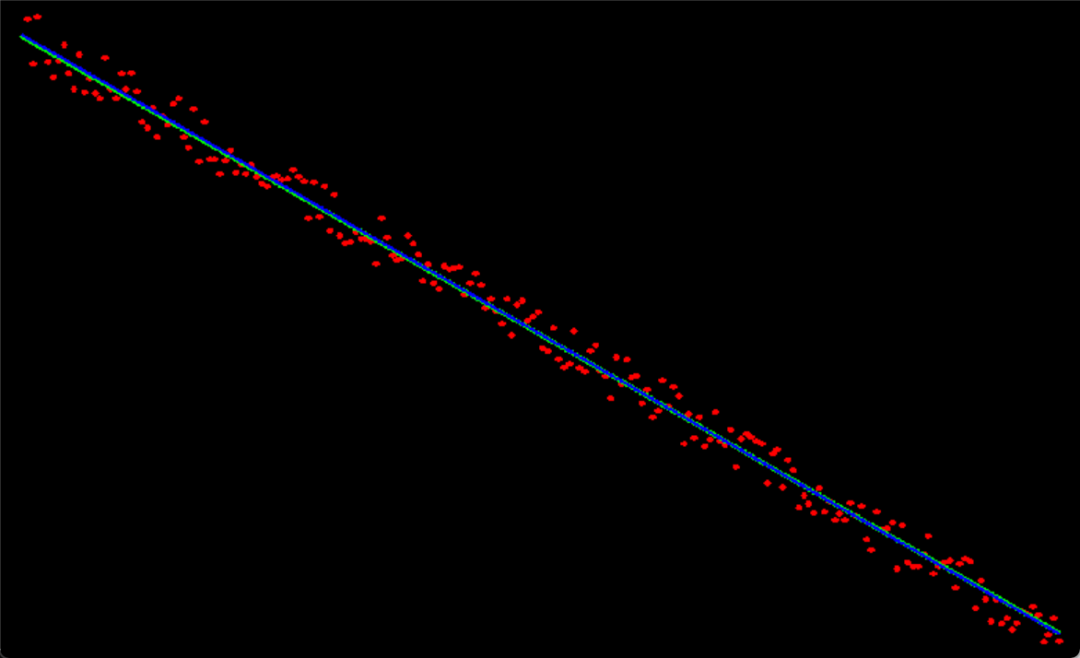
当离群点比较少时，最小二乘直线拟合算法与结合最小二乘、RANSAC的直线拟合算法结果差不多，如下图，蓝线为最小二乘直线拟合算法的结果，绿线为结合最小二乘、RANSAC的直线拟合算法的结果，两线基本重合。

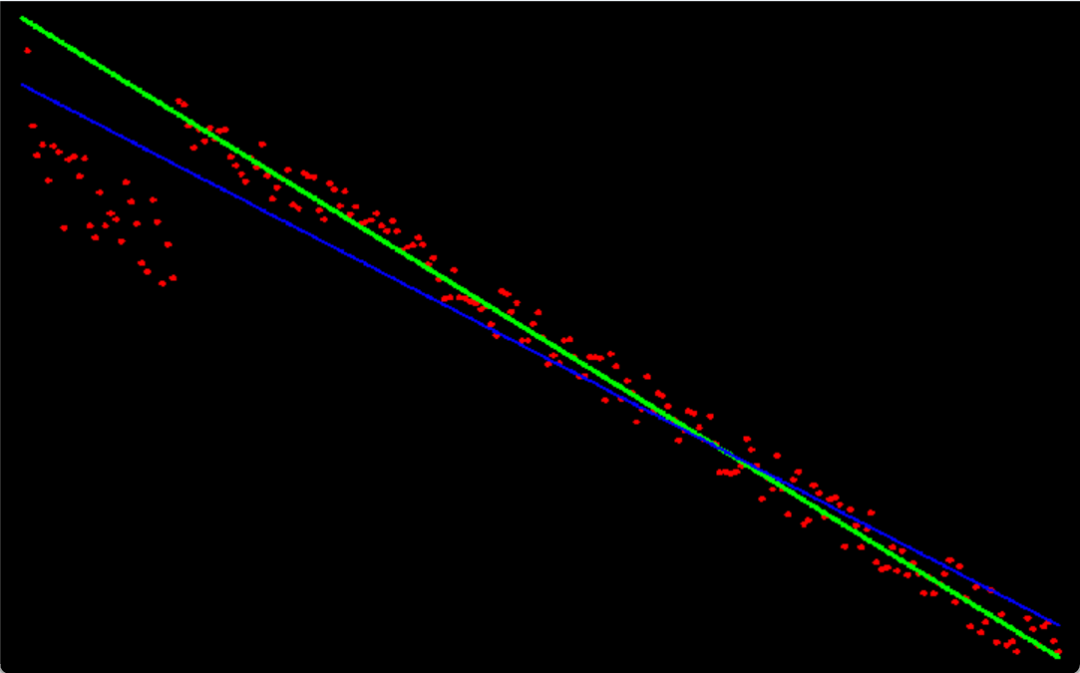
当离群点比较多时，最小二乘直线拟合算法的结果会出现较大偏差（蓝线），结合最小二乘、RANSAC的直线拟合算法则不会（绿线）：

—

题外话

个人要把一个公众号做好做大真的很难，之前也是疲惫了吧，再加上工作也比较忙，所以好久不更新公众号了。现在决定继续更新，是因为看到自己的公众号虽然很久没更新但还能陆陆续续帮助到一些人，心里面还是很开心的，这不就是自己的初心吗：提升自己，总结自己，帮助他人。

看到这里的你，如果觉得我的文章对你有帮助，麻烦帮帮我做一下宣传和转发，让更多有需要的人看到。你们的肯定是我继续更新地最大动力！

欢迎扫码关注本微信公众号，接下来会不定时更新更加精彩的内容，敬请期待~

基于最小二乘法的直线拟合原理及C++实现

猜你喜欢