迪杰斯特拉算法又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
以下是数据结构中关于迪杰斯特拉算法的操作(编程风格参考严蔚敏版数据结构)。
头文件及宏定义
#include<iostream>
#include<stdio.h>
using namespace std;
typedef char VerTexType;
typedef int ArcType;
#define MaxInt 32767
#define MVNum 100
#define ArcNum 100
#define OK 1
#define ERROR -1
#define NOTPRENODE -1
typedef int status;
说明: NOTPRENODE表示无前驱结点
图以及辅助数组的声明
bool S[MVNum];
int Path[MVNum];
int D[MVNum];
typedef struct{
VerTexType vexs[MVNum] {
'A','B','C','D','E','F'};
ArcType arcs[MVNum][MVNum];
int vexnum = 6,arcnum = 8;
}AMGraph;
说明:
S[MVNum];//记录源点到终点vi的是否已被确定的最短路径长度,true表示确定false表示未确定(换个说法就是:源点到vi的边如果被选中并确定就是true,如果只是被选中并没将vi确定下来则是false)。
…
Path[MVNum];//记录源点到终点vi当前最短路径上vi的直接前驱顶点序号(如果没有前驱则为-1)。比如A(下标为0)、C(下标为2),如果将当前最短路径边选为AC(注意,只是暂选AC而不一定是确定AC,此时Path会更新而S不一定会更新),那么Path[2] = 0。
…
D[MVNum];//记录从源点到终点vi的当前最短路径长度(如果没有弧则为无穷大),其实说白了D就是一个路径权值表。 这个D的值一定要记住,是从源点开始到vi的值!是从源点开始!是从源点开始!例如,AC权值为10,CD(D下标为3)权值为20。假设过程中选择了A到D的最短路径是A->C->D,那么D[3] = 10+20=30。千万别写成那么D[3] = 20,这是错的!
举个例子:
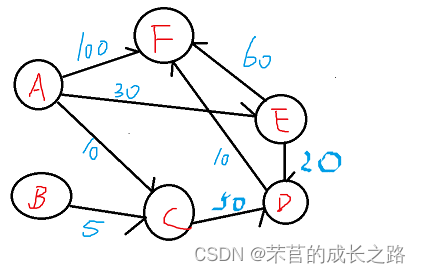
构建有向图
status CreateSDG(AMGraph &G){
//创建有向图
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++){
if(i==j){
G.arcs[i][j] = NOTPRENODE;
}else
G.arcs[i][j] = MaxInt;//初始状态全部节点之间相互不可达
}
}
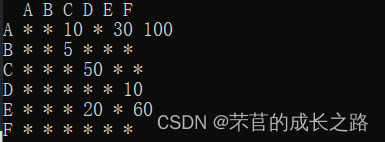
G.arcs[0][2]=10;G.arcs[0][4]=30;G.arcs[0][5]=100;
G.arcs[1][2]=5;
G.arcs[2][3]=50;
G.arcs[3][5]=10;
G.arcs[4][3]=20;G.arcs[4][5]=60;
return OK;
}
注意!有向图的邻接矩阵不一定对称(当有向图的邻接矩阵对称就是其特殊情况无向图)
老样子先生成邻接矩阵:
初始化三个辅助数组(S、Path、D):
void initial(AMGraph &G,VerTexType v0){
int v0i = LocateVex(G,v0);//(v0-index,源点v0的下标)
for(int vi=0;vi<G.vexnum;vi++){
S[vi] = false;//S初始状态为空集
D[vi] = G.arcs[v0i][vi];//将v0到各个终点的最短路径初始化弧上的权值(其实就是先把v0和其它点先强行直连起来)
if(D[vi]<MaxInt&&D[vi]!=0){
Path[vi] = v0i;//如果v0和vi之间有弧,将vi的前置节点设为v0。
} else{
Path[vi] = NOTPRENODE;
}
} //for
S[v0i] = true;//将v0加入S;
D[v0i] = 0;//源点到源点自身的距离为0
}
第一步:S全置false(全部未选)
第二步:把源点和其它点的边录入D中(没有边的以无穷大的形式录入)
第三步:如果源点可以到某个节点,那么该节点的先驱节点设置成源点;否则设置为无前驱节点
第四步:将源点的S置true(表示源点已被选择),源点到源点自己的距离D设为0。
迪杰斯特拉(Dijkstra)核心算法
void Dijkstra(AMGraph &G,VerTexType v0){
int v0i = LocateVex(G,v0);
//每次求得v0到某个顶点v的最短路径,将v加到S集
for(int i=1;i<G.vexnum;i++){
//对其余的n-1个点进行计算
int min = MaxInt;
int t;//中间变量
for(int j=0;j<G.vexnum;j++){
if(!S[j]&&D[j]<min){
//选出一条最短的路径,终点为j
t = j;//记录节点j
min = D[j];//当前最短路径权值是D[j]
}//if
} //for
S[t] = true;//终点t已被选择
for(int j=0;j<G.vexnum;j++){
//更新从v0出发到其它点集合上所有最短路径长度
if(!S[j]&&(D[t]+G.arcs[t][j]<D[j])){
//如果源点经过t点到j的距离小于源点直接到j点的距离。
D[j] = D[t]+G.arcs[t][j];//更新D
Path[j] = t;//更改前驱为t。
}
}
}//for
}
第一步:作n-1重循环(对除源点以外的节点进行遍历)
第二步:在当前路径权值表D中选出权值最短的边,记录该边的终点vi,并将该点vi的S设为已选择
第三步:将源点直接到剩下未被选择的节点vj的距离与源点经过vi节点再到未被选择的节点vj的距离进行比较(此时vi充当一个中间节点的作用),如果源点直接到vj的距离短则不作操作(初始化的时候已经操作完毕了),如果源点经过vi到达vj的距离更短,则将D[j]的距离修改为源点到vi的距离加上vi到vj的距离,那么vj点的前驱就从源点变成了vi(因为源点要经过vi到vj了)。重复第二第三步,直到选出源点分别到全部节点的最短路径(D的最后数据就是最短路径结果)。
用上例图进行手推运行过程(天蓝色表示S,绿色表示选出边但未确认终点,深蓝色表示选出边且确认终点,紫色表示该节点的前驱节点):
1、三个辅助数组的初始化:
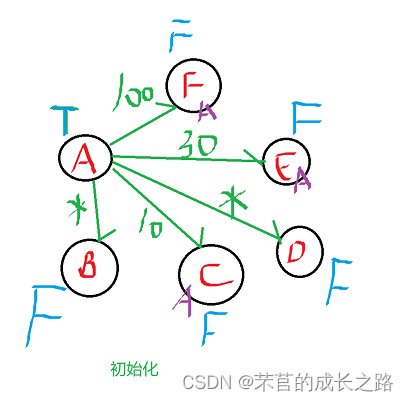
2、第一次大循环:AC权值最小,选择AC。C设置为已选择。
进行小循环:ACB的权值不小于AB,不进行操作;AD的权值小于ACD(下标为3)的权值,修改D【3】=AC+CD = 10+50 = 60,D的前驱结点修改为C。注意:D【3】表示为AD距离为60了。AE的权值30小于ACD权值,不进行操作;AF权值100小于ACF权值,不进行操作。
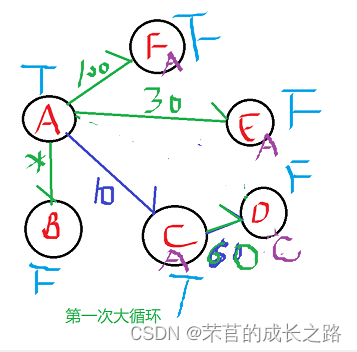
3、第二次大循环:AE权值30最短,选择AE(下标4),将E标记为已选择。
进行小循环:AEB权值不小于AB,不作操作;AED权值30+20=50小于AD权值(D下标为3),修改D【3】=50(意思是AD距离为50),D的前驱结点修改为E;AEF权值30+60=90小于AF(下标5)的权值100,修改D【5】=90(意思是AF距离为50),F前驱节点修改为为E;
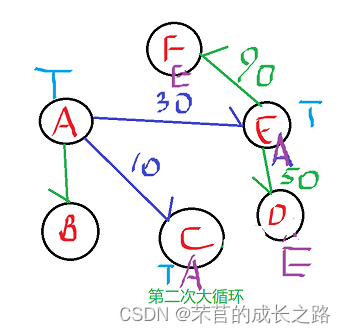
4、第三次大循环:选出AED权值50最小,选出AD,D标记为已选择。
进行小循环:ADB权值不小于AB,不进行操作;ADF权值50+10=60小于AF的权值90,D【5】=60(意思是AF距离为60),将F的前驱结点设置成E;
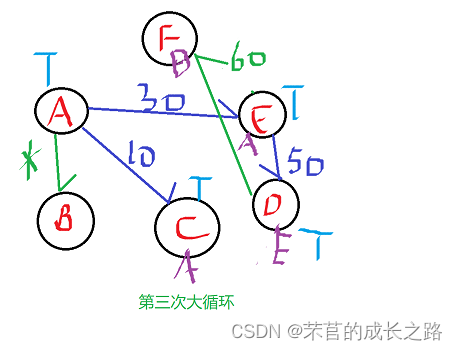
5、第四次大循环:选出最短边AF权值60,将F标记已被选择。
进行小循环:AFB的权值不小于AB的权值,不作操作。
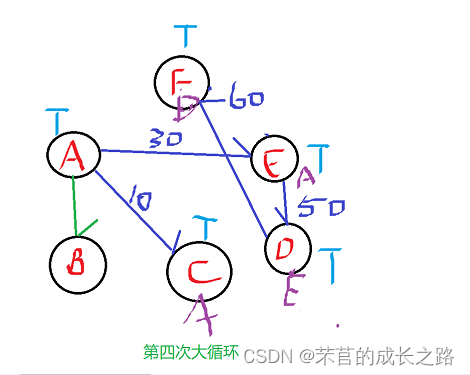
第五次大循环:未选择的边只有AB边了,但是由于AB的没有变(距离为无穷大),B不能被选择。
因为全部节点都被已被选择,小循环不作任何操作。程序结束(所以B的前驱结点一直都是NOTPRENODE)。
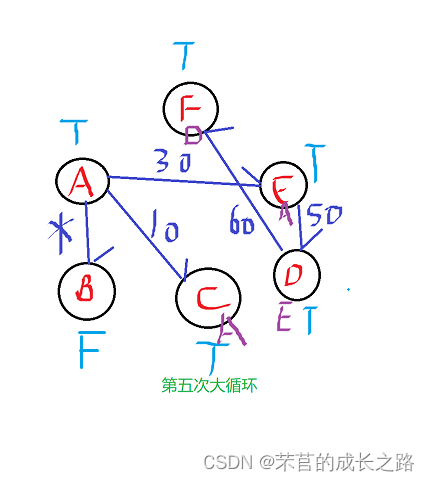
运行结果
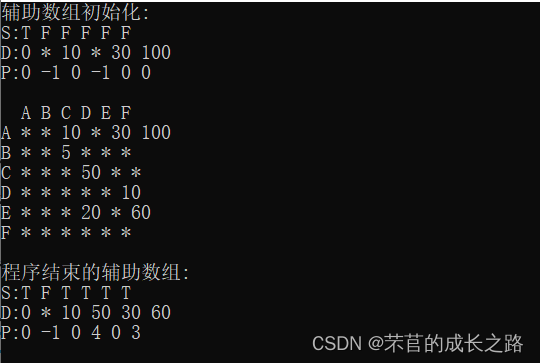
源代码
#include<iostream>
#include<stdio.h>
using namespace std;
typedef char VerTexType;
typedef int ArcType;
#define MaxInt 32767
#define MVNum 100
#define ArcNum 100
#define OK 1
#define ERROR -1
#define NOTPRENODE -1
typedef int status;
bool S[MVNum];//记录源点到终点vi的是否已被确定的最短路径长度,true表示确定false表示未确定
int Path[MVNum];//记录源点到终点vi当前最短路径上vi的直接前驱顶点序号(如果没有前驱则为-1)
int D[MVNum];//记录从源点到终点vi的当前最短路径长度(如果没有弧则为无穷大)。
typedef struct{
VerTexType vexs[MVNum] {
'A','B','C','D','E','F'};
ArcType arcs[MVNum][MVNum];
int vexnum = 6,arcnum = 8;
}AMGraph;
status CreateSDG(AMGraph &G){
//创建有向图
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++){
if(i==j){
G.arcs[i][j] = NOTPRENODE;
}else
G.arcs[i][j] = MaxInt;//初始状态全部节点之间相互不可达
}
}
G.arcs[0][2]=10;G.arcs[0][4]=30;G.arcs[0][5]=100;
G.arcs[1][2]=5;
G.arcs[2][3]=50;
G.arcs[3][5]=10;
G.arcs[4][3]=20;G.arcs[4][5]=60;
return OK;
}
void ShowGraph(AMGraph G){
cout<<" ";
for(int i=0;i<G.vexnum;i++){
cout<<" "<<G.vexs[i];
}
cout<<endl;
for(int i=0;i<G.vexnum;i++){
cout<<G.vexs[i]<<" ";
for(int j=0;j<G.vexnum;j++){
if(G.arcs[i][j]==MaxInt||G.arcs[i][j]==NOTPRENODE){
cout<<"* ";
}else{
cout<<G.arcs[i][j]<<" ";
}
}
cout<<endl;
}
}
int LocateVex(AMGraph G, VerTexType v){
int i;
for(i=0;i<G.vexnum;i++){
if(G.vexs[i]==v){
return i;
}
}
return ERROR;
}
void initial(AMGraph &G,VerTexType v0){
int v0i = LocateVex(G,v0);//(v0-index,源点v0的下标)
for(int vi=0;vi<G.vexnum;vi++){
S[vi] = false;//S初始状态为空集
D[vi] = G.arcs[v0i][vi];//将v0到各个终点的最短路径初始化弧上的权值(其实就是先把v0和其它点先强行直连起来)
if(D[vi]<MaxInt&&D[vi]!=0){
Path[vi] = v0i;//如果v0和vi之间有弧,将vi的前置节点设为v0。
} else{
Path[vi] = NOTPRENODE;
}
} //for
S[v0i] = true;//将v0加入S;
D[v0i] = 0;//源点到源点自身的距离为0
}
void Dijkstra(AMGraph &G,VerTexType v0){
int v0i = LocateVex(G,v0);
//每次求得v0到某个顶点v的最短路径,将v加到S集
for(int i=1;i<G.vexnum;i++){
//对其余的n-1个点进行计算
int min = MaxInt;
int t;//中间变量
for(int j=0;j<G.vexnum;j++){
if(!S[j]&&D[j]<min){
//选出一条最短的路径,终点为j
t = j;//记录节点j
min = D[j];//当前最短路径权值是D[j]
}//if
} //for
S[t] = true;//终点t已被选择
for(int j=0;j<G.vexnum;j++){
//更新从v0出发到其它点集合上所有最短路径长度
if(!S[j]&&(D[t]+G.arcs[t][j]<D[j])){
//如果源点经过t点到j的距离小于源点直接到j点的距离。
D[j] = D[t]+G.arcs[t][j];//更新D
Path[j] = t;//更改前驱为t。
}
}
}//for
}
void show(){
cout<<"S:";
for(int i=0;i<6;i++){
if(S[i]){
cout<<"T ";
}else{
cout<<"F ";
}
}
cout<<endl;
cout<<"D:";
for(int i=0;i<6;i++){
if(D[i]==MaxInt){
cout<<"*"<<" ";
continue;
}
cout<<D[i]<<" ";
}
cout<<endl;
cout<<"P:";
for(int i=0;i<6;i++){
cout<<Path[i]<<" ";
}
cout<<endl;
}
int main(){
AMGraph G;
CreateSDG(G);
initial(G,'A');
cout<<"辅助数组初始化:\n";
show();
cout<<endl;
Dijkstra(G,'A');
ShowGraph(G);
cout<<endl;
cout<<"程序结束的辅助数组:\n";
show();
return 0;
}
时间复杂度与空间复杂度
时间复杂度: 迪杰斯特拉算法的时间复杂度为 O(n×n),其中 n 表示节点个数,当图 中节点越多时,迪杰斯特拉算法花费的时间就越多。
空间复杂度: 迪杰斯特拉算法的空间复杂度也是 O(n×n),其中 n 表示节点个数,当 图中节点越多时,迪杰斯特拉算法的空间复杂度也就越大。
敬请批评指正!