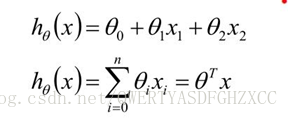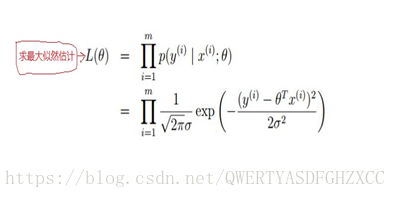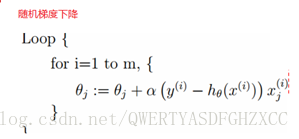在介绍线性回归前,先介绍下一些会用到的相关概念。
满秩矩阵
矩阵的秩的定义:
用初等行变换将矩阵A化为阶梯形矩阵, 则矩阵中非零行的个数就定义为这个矩阵的秩, 记为r(A),根据这个定义, 矩阵的秩可以通过初等行变换求得。需要注意的是, 矩阵的阶梯形并不是唯一的, 但是阶梯形中非零行的个数总是一致的。
满秩矩阵的定义:
设A是n阶矩阵, 若r(A) = n, 则称A为满秩矩阵。满秩矩阵是一个很重要的概念, 它是判断一个矩阵是否可逆的充分必要条件。
注:
1、线性回归的损失函数是凸函数,只有一个全局最小值,那么当损失函数关于W的导数为0时,就得到了最优解。
2、因为在矩阵求解W时,最终会得到W=(XTX)-1XTy,需要求解XTX的逆矩阵,所以需要XTX是满秩矩阵。
最小二乘法
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
大数定律
在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。
中心极限定理
中心极限定理,是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础,指出了大量随机变量近似服从正态分布的条件。它是概率论中最重要的一类定理,有广泛的实际应用背景。在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。中心极限定理就是从数学上证明了这一现象。最早的中心极限定理是讨论重点,伯努利试验中,事件A出现的次数渐近于正态分布的问题。
高斯分布
若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布,且其概率密度函数为
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作X~N(μ,σ2),读作X服从N(μ,σ2),或X服从正态分布。
极大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!
1、线性回归
线性回归主要用来解决连续值预测的问题。
线性回归到底在干什么?
因为我们对于一个数据集,不明确其之间的关系,所以需要构造一个函数,进行拟合数据,拟合后便可以实现取任意点进行值的预测。所以这里我们采用线性的函数进行拟合,和求解这个线性函数的参数的过程,以及将参数最优化就是线性回归算法在干的事情。
1.1、线性回归问题
一元线性回归分析:y=ax+b,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示。
多元线性回归分析:hθ(x)=θ0+θ1x1+...+θnxn,包括两个或两个以上的自变量,并且因变量和自变量是线性关系。
1.2、线性回归介绍
定义:线性回归在假设特证满足线性关系,根据给定的训练数据训练一个模型,并用此模型进行预测。为了了解这个定义,我们先举个简单的例子;我们假设一个线性方程 Y=2x+1, x变量为商品的大小,y代表为销售量;当月份x =5时,我们就能根据线性模型预测出 y =11销量;对于上面的简单的例子来说,我们可以粗略把 y =2x+1看到回归的模型;对于给予的每个商品大小都能预测出销量;当然这个模型怎么获取到就是我们下面要考虑的线性回归内容;并且在现实中影响销量(y)的因素好有很多,我们就拿商品大小(x₁),商品价格为例 (x₂)为例:
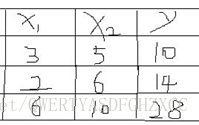
在机器学习之前,获取数据是第一步(无米难巧妇之炊),假定我们的样本如下:其中x1 为商品的大小,x2 为商品的价格,y 为商品的销量;
1.3、模型推导
为了推导模型,在假设数据满足线性模型条件下,可以设定线性模型为;x1特征为商品的大小,X2特征为商品的价格;
模型假定好后,我们把训练数据代入上面的设定模型中,可以通过模型预测一个样本最终值;
然后样本真实值 y 和模型训练预测的值之间是有误差 ε,再假设训练样本的数据量很大的时候,根据中心极限定律可以得到 ∑ε 满足(u ,δ²)高斯分布的;由于方程有截距项 ,故使用可以 u =0; 故满足(0,δ²)的高斯分布;
如上面可知,对于每一个样本 x ,代入到 p (y|x ;θ) 都会得到一个y 的概率;又因为设定样本是独立同分布的;对其求最大似然函数:
对其化简如下:
以上就得到了回归的损失函数最小二乘法的公式,对于好多介绍一般对线性回归的线性损失函数就直接给出了上面的公式二乘法。下面我们就对上面做了阶段性的总结:线性回归,根据大数定律和中心极限定律假定样本无穷大的时候,其真实值和预测值的误差ε的加和服从u=0,方差=δ²的高斯分布且独立同分布,然后把ε =y-Øx 代入公式,就可以化简得到线性回归的损失函数;
第二步:对损失函数进行优化也就是求出w,b,使的损失函数最小化;
第一种方法使用矩阵(需要XTX满足可逆条件)
第二种方法是使用梯度下降法
总体流程就如上所示,就是求出每个变量的梯度;然后顺着梯度方向按一定的步长a,进行变量更新;下面我们就要求出每个变量的梯度,下面对每个θ进行梯度求解公式如下:
如上我们求出变量的梯度;然后迭代代入下面公式迭代计算就可以了:
上面每次更新变量,都要把所有的样本的加起来,数据量大的时候效率不高,下面还有一种就是按单个样本进行优化,就是随机梯度下降:
比如:一个输入样本是2维的。形式如[a,b] ,则二阶多项式的特征集如下[1,a,b,a^2,ab,b^2]。
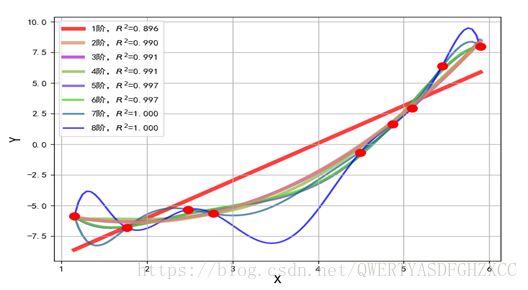
使用1-8阶的多项式特征的模型效果如下:
从上面图像可以看出,当模型复杂度提高的时候,对训练集的数据拟合很好,但会出现过度拟合现象,为了防止这种过拟合现象的出现,我们在损失函数中加入了惩罚项,根据惩罚项不同分为以下:
最后一个为Elastic Net 回归,把 L1 正则和 L2 正则按一定的比例结合起来:
L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下,选择Lasso比较合适,因为它能自动选择特征。而如果所有特征中,大部分特征都能起作用,而且起的作用很平均,那么使用Ridge也许更合适。对于各种回归的比较可以看下图: