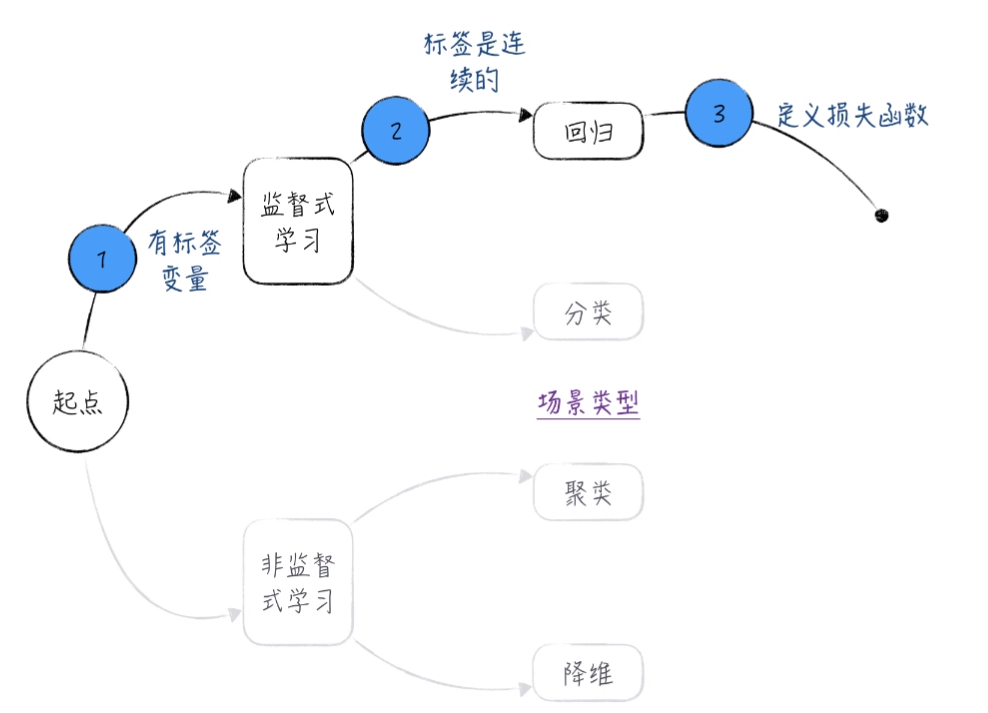
1. 机器学习眼中的线性回归
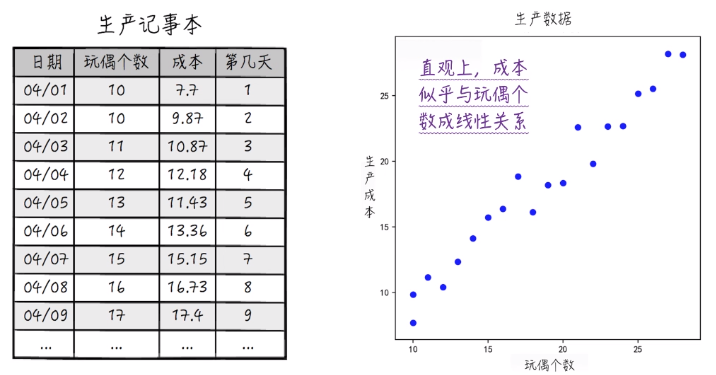
左图是原始建模数据，目的是用来寻找玩偶数量和成本的某种关系。右图将数据可视化得到散点图。
第一步 进行场景确定
第二步 定义损失函数
建模的目的：模型预测值与真实值之间的差距越小越好。下面有两种定义损失函数的方法。带“帽子”的变量代表预测值。不带的表示观测值。
由于以上两点原因，所以采用右边的函数作为损失函数。
实际上使用左面的函数定义损失函数也能得到一个线性模型，只是并不是我们常说的线性回归模型而已。
所以：损失函数是机器学习模型的核心。（即使相同的模型形式，不同的损失函数对应着不同模型的效果）。
如果把模型看成是人工智能，那么损失函数就是它的三观。
题外话：
由于模型的损失函数是由人定义的，那么从伦理的角度来讲，不能再将“技术无罪”作为作恶的借口和理由，特别是在模型日益成为我们生活主宰的今天。
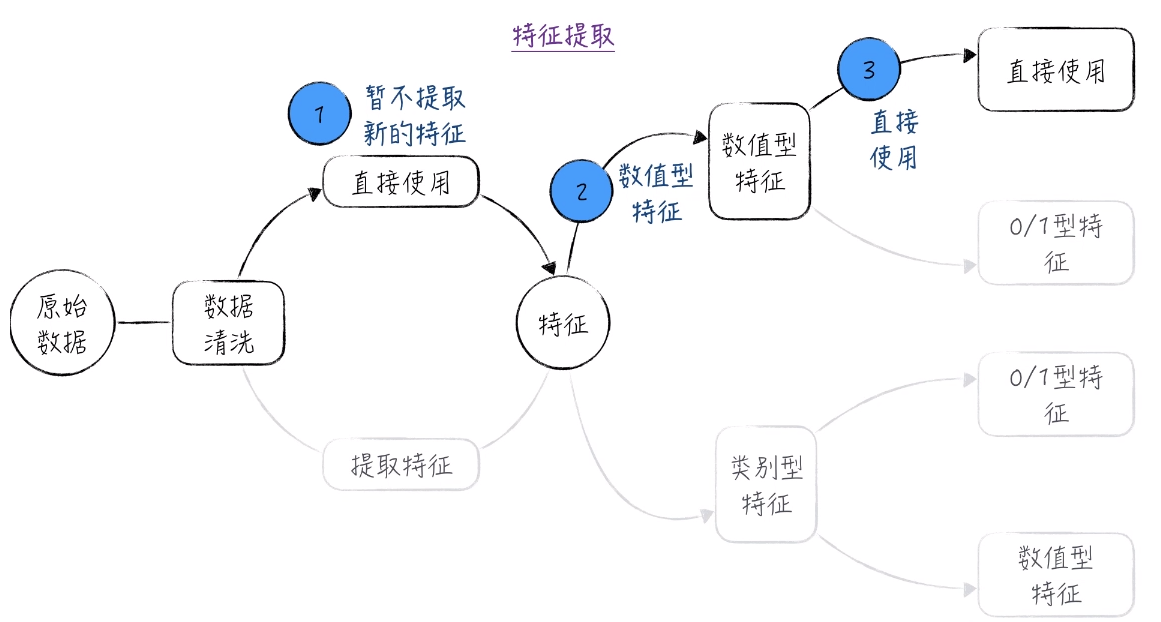
第三步 特征提取
原始数据比较干净，所以并不需要进行数据清洗。在本题中玩偶个数可以作为特征直接使用。
第四步 确定模型形式和参数估计
第五步 评估模型效果
对于回归问题，常用的模型评估指标有两个：
- 均方差（MSE）：预测值与真实值的平均差距。L指的是上面定义的损失函数。
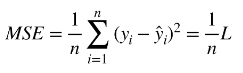
- 决定系数（R2）：数据变化被模型解释的比例。
第一个公式为成本变化幅度。即真实值与真实值平均值之间的差值的平方和。
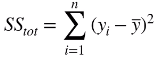
第二个公式是未被模型所解释的变化幅度。即真实值与预测值之间的差值的平方和。从建模的角度来讲，我们希望该公式得到的值越小越好。
所以，决定系数的公式如下：结果越接近于1，模型的预测效果越好。
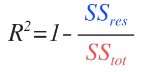
2. 统计眼中的线性回归
2.1 模型的假设
在机器学习的角度，我们并不太关心 x 和 y 的数学关系是怎么样的。整个的建模过程是机械化的。我们只是关心能用什么样的公式能让从 x 出发的预测值与真实值 y 之间的关系最小的可以了。
站在统计学的角度出发，我们试图弄清楚变量 y 与 x 之间的数学关系。
比如 04/01 和 04/02 两天的玩偶个数都是10，但前者成本为7.7，后者成本为9.87.这说明变量 y 似乎带有某种随机性。并且在散点图中，我们同样得到 x 与 y 似乎存在某种线性关系。
在上面公式的基础上，进一步假设。其中假设的 第二点 和 第三点 可能与现实情况冲突。
根据这三个假设我们可以进一步来分析为什么会存在 x 相同而 y 不同的情况。
首先假设模型的 a, b, σ（假设1：随机扰动项服从的正态分布的方差）是已知的。这时候我们可以看到 y 是由 ax + b + 随机值 构成，那么就说明 y 本身就是一个随机值。而且也可以很清楚的证明 yi 是服从 期望为 10a+b 方差为 σ2 的正态分布。所以，有 相同的玩偶个数，不同的成本 这种情况出现正是因为 成本分别是同一正态分布的两次独立观测值。
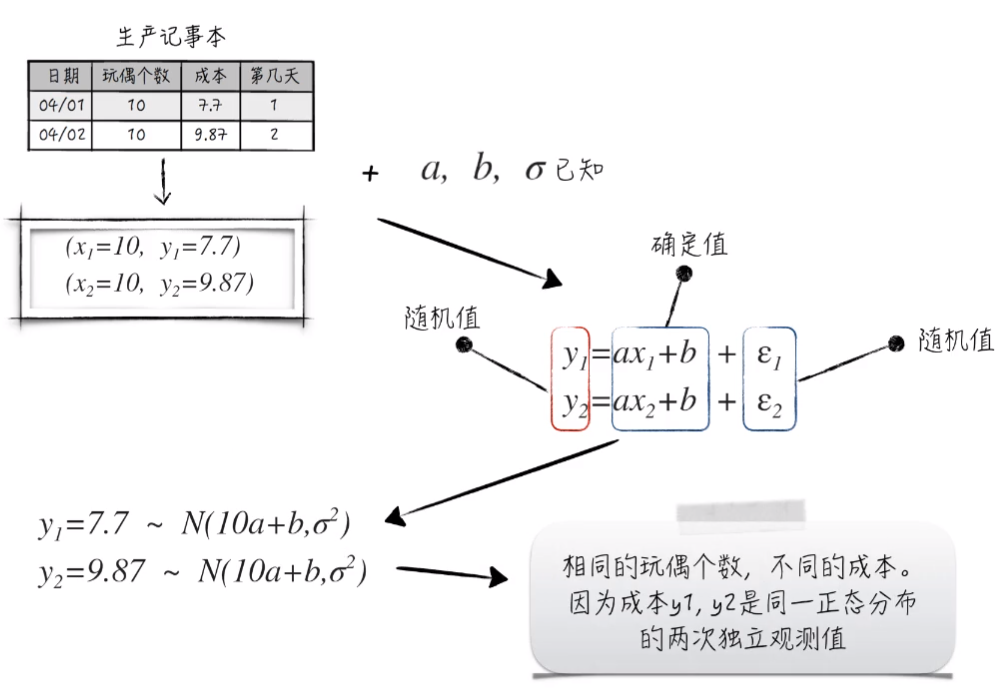
所以，在统计学的眼里，我们得到的变量值其实是一个随机变量的观测值，它并不是一个确定的值。因此，统计学希望通过这样一个随机变量的观测值去挖掘真实的值是多少。
2.2 参数估计公式（最大似然估计法 Maximum Likelihood Estimation, MLE）
根据上面的模型假设，可以得到：
由于 y 是随机变量，就可以定义参数的似然函数（Likelihood function）：
这里的似然函数 L 其实就是 y 的联合条件概率。并且 yi 是相互独立的，那么就可以将似然函数 L 改写成每一点概率的乘积的形式。这一点可以极大地方便后面的数学处理。
既然 y 是随机变量，那么模型参数估计的原则就是 y出现的概率达到最大。
这就是所谓的 最大似然估计法（Maximum Likelihood Estimation, MLE）。
2.3 最大似然估计法与机器学习模型参数估计公式的关系
在机器学习中，首先定义了损失函数，也就是模型真实值与预测值之间的差距。
在机器学习中，参数估计的原则就是使 损失函数达到最小值。
而在统计学中，我们从 y 是随机变量这一点出发，参数估计的原则就是使 y出现的概率达到最大。
将统计学中的最大似然估计法翻译成公式：
由于 L 这里是乘积的形式：
那么为了数学上好处理，引入自然对数函数，也就是以 e为底（2.71828...）的对数函数。对于它有以下性质：
同时，我们也注意到自然对数函数本身是一个增函数，也就是说 L 达到最大值的时候 ln(L) 也达到最大值，因此可以把寻找参数 a, b 的公式改写为：
从之前已经证明 yi 服从正态分布，因此将 lnL 展开，得到如下的式子：
我们可以注意到 前面（一个红线）是一个固定的值，后面（两个红线）才是变量。如果我们想要 lnL 达到最大值，那么我们就要后面的变量达到最小值。所以最终的参数估计公式也就变成了：
这就与前面机器学习里面的 线性回归模型（最小二乘法OLS）的参数估计公式相同。
在之前机器学习的讨论中，我们知道 只要定义一种不同的损失函数，就有一种新的线性回归模型。那么为什么我们通常使用的就是 最小二乘法（OLS）线性回归模型呢？
就是因为它使用的损失函数背后有极为强大的数学基础。
由于 最大似然估计法 与 OLS线性回归模型 的参数估计公式是相同的，所以它们得到的结果是一样的。
2.4 置信区间
根据 2.3 的讨论，我们有了模型参数估计值的公式：
根据模型参数估计公式，可以得到参数 a, b 的估计值。但是，使用不同数据训练模型的时候，会得到不同的参数估计值。（这里的不同的数据，指的是符合同一规律的数据）。
例如：我们采用 04/01，04/02，04/03 和 04/04，04/05，04/06 日期的数据分别训练模型可得到两个估计值，而且这两个值是不相同的：
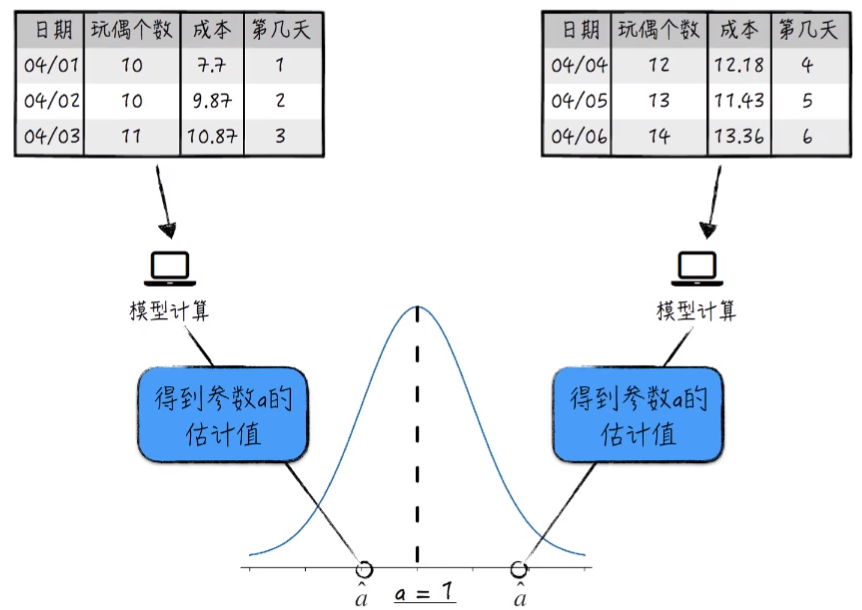
这是因为 模型参数的估计值只是一个随机变量，具体数值依赖于使用的数据。而且数学上可以证明，参数估计值本身是随机变量，并且服从正态分布。
数学上的证明较为繁琐，所以这里就采用一个实证的例子：
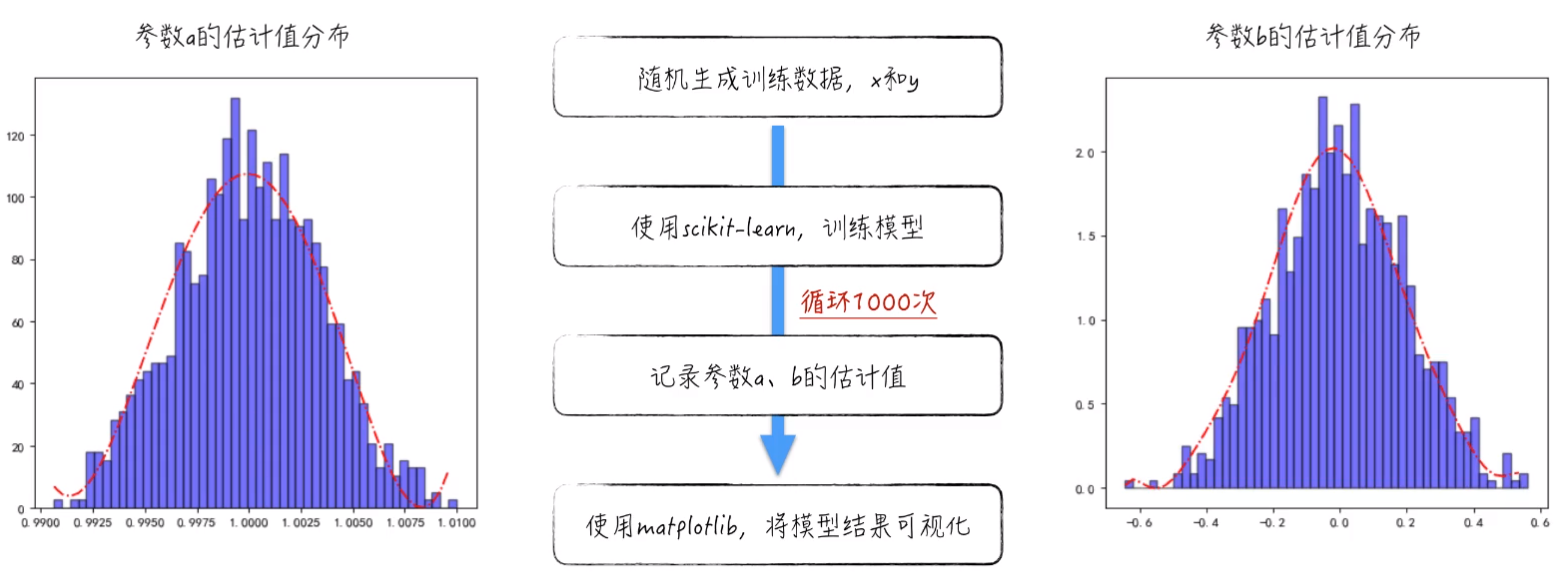
既然得到的估计值只是随机变量的一次观测值，那么我们更关心这个估计值离真实值有多远？
在统计学里，解决方案就是 定义参数真实值的置信区间。
在上面的证明，我们可以得知估计值服从以真实值为期望的正态分布。参数的真实值就是 a 。我们假设这个正态分布的方差为σ2，那么大部分估计值就会落在以 真实值a 为中心，2倍 σ 为半径的区间里面。
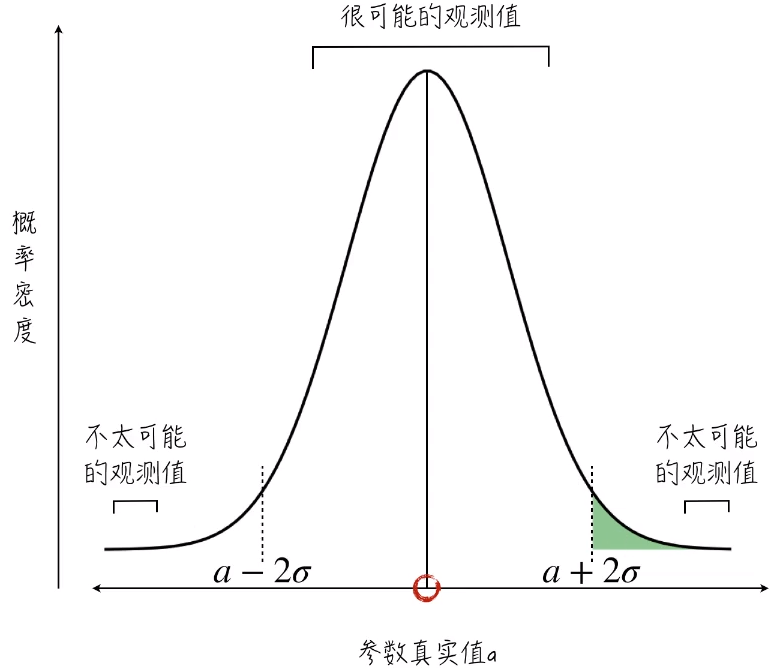
将其翻译为数学公式，即为：
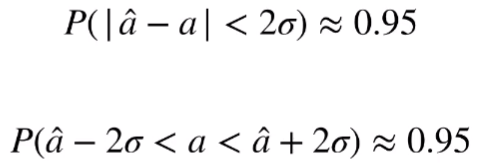
因此，可以定义参数 a 的 95% 的置信区间：
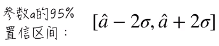
所以，95%的置信区间表示：
重复100次的模型训练，并按公式得到置信区间，那么有95次，参数 a 的真实值将落在这个区间里。
也可以 “通俗地” 理解为参数 a 的大概取值范围。
后面一句话其实不太严谨，因为一开始 假设 参数 a 的真实值是一个确定的值，但是现在又说大概的范围，这又将参数 a 作为一个随机值进行处理，这前后是矛盾的。不过，依然可以这样通俗的进行理解。
置信区间就是控制模型结果随机性的一个工具。也就是说我们得到的参数的估计值其实是一个随机变量。它并不等于真实值，但是我们可以用置信区间去控制这个真实值大概所在的区间范围是多少。
2.5 假设检验
除了置信区间外，还可以使用假设检验来得到更有把握的结果。