考研 | 组成原理【第二章】数据的表示和运算
I. 数制与编码
a. 进位计数制及其相互转换
- 整数部份十进制转二进制: 留意高低位排序

- 小数部分十进制转二进制: 留意高地位排序
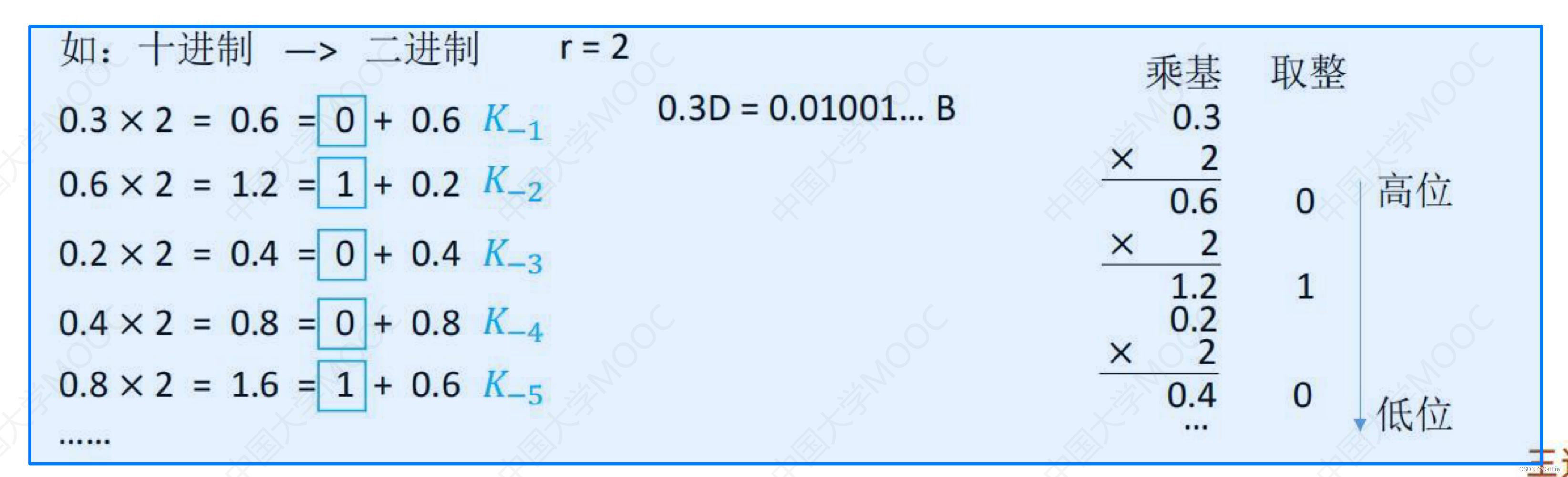
b. BCD码
BCD码: 就是 Binary-Coded Decimal, 即二进制编码的十进制数
1. 8421码
8421码: 就是对于 0~9 每个数字用 4 位二进制数来进行一一表示;其中 8421 码也叫有权码,从左往右数,第一个 1 权值为 8 ;第二个 1 权值为 4;第三个 1 权值为 2;第四个 1 权值为 1;

| 十进制 | 5 | + | 8 | = | 1 | 3 |
|---|---|---|---|---|---|---|
| 二进制 | 0101 | + | 1000 | = | 0001 | 0011 |
2. 余3码
余3码: 属于无权码,它是在 8421码 的基础上,每位加 ( 3 ) 10 (3)_{10} (3)10,即二进制 ( 0011 ) 2 (0011)_2 (0011)2

3. 2421码
2421码: 同 8421码,都属于有权码,但是与 8421码 不同,从右往左数,每个 1 的权值分别为 2421

c. 无符号整数表示和运算
1. 表示

- 全部二进制位都是数值位, 没有符号位, 第 i i i 位的位权是 2 i − 1 2^{i-1} 2i−1
- n n n bit无符号整数表示范围 0 ∼ 2 n − 1 0\sim2^{n}-1 0∼2n−1, 超出则溢出
- 最小数是全 0; 最大数是全 1
2. 运算
- 加法: 从 最低位 开始, 按位相加, 并往更高位进位
- 减法:
- “被减数” 不变, “减数” 全部位按位取反, 末位+1(即变补码), 减法变加法
- 从 最低位 开始, 按位相加, 并往 更高位 进位.
d. 带符号整数的表示和运算
1. 原码
对于 n + 1 n+1 n+1 位机器字长:
- 最高位为符号位, “0/1” 对应 “正负”; 剩余位数为数值位, 表示真值的绝对值
- 表示范围 − ( 2 n − 1 ) ≤ x ≤ 2 n − 1 -(2^n-1) \leq x \leq 2^n-1 −(2n−1)≤x≤2n−1
- 真值 0 有两种形式, [ + 0 ] 原 = 0 , 00000000 ; [ − 0 ] 原 = 1 , 00000000 [+0]_原=0,00000000; [-0]_原=1,00000000 [+0]原=0,00000000;[−0]原=1,00000000
缺点: 符号位不能参与运算, 需要设计复杂的硬件电路才能处理

2. 反码
在 原码 的基础上: 正数不变; 负数 符号位不变数值位取反

3. 补码
-
机器的方式: 原 → 反 → 补 (反码转补码: 正数不变, 负数末位+1)

-
人工手算的方式: 原 → 补
正数不变; 负数从右往左找到第一个1,这个1左边的所有数值位按位取反;
补码 转 原码 也是这种方式, 正数不变, 负数从右往左找到第一个 1, 这个 1 左边的所有数值位按位取反

-
这里记录一个我自己总结的直接从负数补码算真值的方法:
见上图右下角 蓝色部分- 从右往左找到第一个1
- 这个 1 左边的所有 0 对应的二进制权值 + 这个 1 对应的二进制权值 = 真值
-
补码加法: 从最低位开始, 按位相加(包括符号位), 并往更高位进位
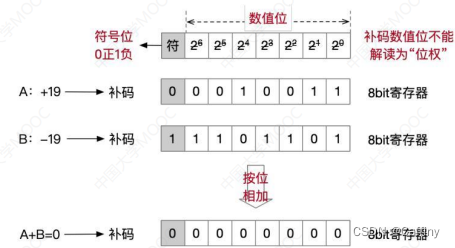
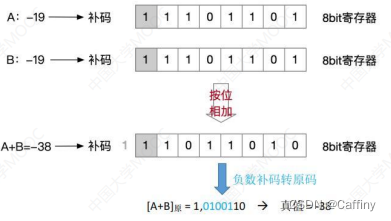
-
补码减法:
- “被减数” 不变, “减数” 全部按位取反(包括符号位)末位+1
- 减法变加法, 从最低位开始, 按位相加, 并往更高位进位


4. 移码
移码: 在补码的基础上, 符号位取反; 注意: 只能表示正数

5. 原反补移码特性对比
-
转换关系:

-
表示范围:

-
用几种码来表示整数:

e. 定点小数的表示和运算
1. 定点小数 v.s. 定点整数
注意: 定点小数第一位是符号位, 即小数点前一位; 定点小数不能用移码表示

2. 定点小数的加法运算
同定点整数加法: 从最低位开始, 按位相加(包括符号位), 并往更高位进位;

3. 定点小数的减法运算
同定点整数减法: "被减数"不变, 全部位按位取反, 末位+1, 减法变加法

II. 运算方法和运算电路
a. 基本运算部件
1. 逻辑运算
-
与 | 或 | 非

-
与非 | 或非 | 异非 | 同或

-
用 与或非 组合实现异或门

-
简化逻辑表达式
- 优先级: 与 > 或
- 分配律: A ( C + D ) = A C + A D A(C+D)=AC+AD A(C+D)=AC+AD
- 结合律: A B C = A ( B C ) ABC=A(BC) ABC=A(BC); A + B + C = A + ( B + C ) A+B+C=A+(B+C) A+B+C=A+(B+C)
- 反演律: A + B ‾ = A ‾ ⋅ B ‾ \overline{A+B}=\overline{A}\cdot\overline{B} A+B=A⋅B; A ⋅ B ‾ = A ‾ + B ‾ \overline{A\cdot B}=\overline{A}+\overline{B} A⋅B=A+B
2. 一位全加器
一位全加器实现的功能是 一个二进制位 上的加法, 不仅要结合当前两个加数的二进制位, 还要结合从前一个二进制位带上来的 进位.
- 加法结果 S i S_i Si: 看输入(两个加数的二进制位, 前一位的进位) 中有偶数个 1 还是 奇数个 1
S i = A i ⊕ B i ⊕ C i − 1 S_i = A_i \oplus B_i \oplus C_{i-1} Si=Ai⊕Bi⊕Ci−1 - 向高位的进位 C i C_i Ci: 如果输入中至少有两个 1, 进位就是 1
C i = A i B i + ( A i ⊕ B i ) C i − 1 C_i = A_iB_i+(A_i\oplus B_i)C_{i-1} Ci=AiBi+(Ai⊕Bi)Ci−1
第一项代表的是 两个加数的二进制位 都是1
第二项代表两个本位中只有一个 1 , 且来自低位的进位是 1
用逻辑电路图表示:

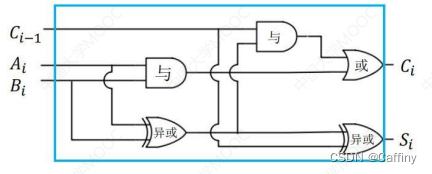

3. 串行加法器
串行加法器: 只由一个 一位全加器 构成, 两个加数 按位 一个一个二进制位送入 全加器 里面进行运算, 这种就是 串行. 如果操作数长 n n n 位, 加法器就要进行 n n n 次运算.


4. 串行进位的并行加法器
串行进位的并行加法器: 把 n n n 个 全加器 串连起来, 就可以得到两个 n n n 位二进制数相加的结果

从图中看得出来, 缺点很明显, 由于每一级的输入除了两个加数自身的二进制数以外, 还要包括上一位的进位, 因此每一级的加法都得依赖上一级.
5. 并行进位的并行加法器
并行进位的并行加法器 其实就是在 串行的基础上耍了一些trick. 前面提到, 由于受限于每一级的进位 C i − 1 C_{i-1} Ci−1, 因此我们对 C i C_{i} Ci 进行展开:
C i = A i B i + ( A i ⊕ B i ) C i − 1 C i = A i B i + ( A i ⊕ B i ) ( A i − 1 B i − 1 + ( A i − 1 ⊕ B i − 1 ) C i − 2 ) C i = A i B i + ( A i ⊕ B i ) ( A i − 1 B i − 1 + ( A i − 1 ⊕ B i − 1 ) ( A i − 2 B i − 2 + ( A i − 2 ⊕ B i − 2 ) C i − 3 ) ) \begin{aligned} &C_{i}=A_{i} B_{i}+\left(A_{i} \oplus B_{i}\right) C_{i-1} \\ &C_{i}=A_{i} B_{i}+\left(A_{i} \oplus B_{i}\right)\left(A_{i-1} B_{i-1}+\left(A_{i-1} \oplus B_{i-1}\right) C_{i-2}\right) \\ &C_{i}=A_{i} B_{i}+\left(A_{i} \oplus B_{i}\right)\left(A_{i-1} B_{i-1}+\left(A_{i-1} \oplus B_{i-1}\right)\left(A_{i-2} B_{i-2}+\left(A_{i-2} \oplus B_{i-2}\right) C_{i-3}\right)\right) \end{aligned} Ci=AiBi+(Ai⊕Bi)Ci−1Ci=AiBi+(Ai⊕Bi)(Ai−1Bi−1+(Ai−1⊕Bi−1)Ci−2)Ci=AiBi+(Ai⊕Bi)(Ai−1Bi−1+(Ai−1⊕Bi−1)(Ai−2Bi−2+(Ai−2⊕Bi−2)Ci−3))
当展开到 C 0 C_0 C0 的时候, 整体的 C i C_i Ci 就可以直接确定, 因为每一位的 A i A_i Ai B i B_i Bi 都已经, C i C_i Ci 也已知, 那么就可以直接算得任意一步的进位 C i C_i Ci
我们再让 G i = A i B i G_i=A_iB_i Gi=AiBi P i = A i ⊕ B i P_i=A_i\oplus B_i Pi=Ai⊕Bi
C i = A i B i + ( A i ⊕ B i ) C i − 1 = G i + P i C i − 1 C 1 = G 1 + P 1 C 0 C 2 = G 2 + P 2 C 1 = G 2 + P 2 G 1 + P 2 P 1 C 0 C 3 = G 3 + P 3 C 2 = G 3 + P 3 G 2 + P 3 P 2 G 1 + P 3 P 2 P 1 C 0 C 4 = G 4 + P 4 C 3 = G 4 + P 4 G 3 + P 4 P 3 G 2 + P 4 P 3 P 2 G 1 + P 4 P 3 P 2 P 1 C 0 \begin{aligned} &C_{i}=A_{i} B_{i}+\left(A_{i} \oplus B_{i}\right) C_{i-1}=G_{i}+P_{i} C_{i-1} \\ &C_{1}=G_{1}+P_{1} C_{0} \\ &C_{2}=G_{2}+P_{2} C_{1}=G_{2}+P_{2} G_{1}+P_{2} P_{1} C_{0} \\ &C_{3}=G_{3}+P_{3} C_{2}=G_{3}+P_{3} G_{2}+P_{3} P_{2} G_{1}+P_{3} P_{2} P_{1} C_{0} \\ &C_{4}=G_{4}+P_{4} C_{3}=G_{4}+P_{4} G_{3}+P_{4} P_{3} G_{2}+P_{4} P_{3} P_{2} G_{1}+P_{4} P_{3} P_{2} P_{1} C_{0} \end{aligned} Ci=AiBi+(Ai⊕Bi)Ci−1=Gi+PiCi−1C1=G1+P1C0C2=G2+P2C1=G2+P2G1+P2P1C0C3=G3+P3C2=G3+P3G2+P3P2G1+P3P2P1C0C4=G4+P4C3=G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C0
画成电路图:

6. 补码加减法器
- XY分别对应两个加数或者被减数和减数
- 设置 s u b sub sub, 如果是减法就设置为 1, 如果是加法设置为 0
- 当 s u b sub sub 为0, 即加法的时候, Y 直接通过 多路选择器 进入加法器
- 当 s u b sub sub 为1:
- Y 会先经过 非门, 对Y上的所有位进行按位取反
- 同时, s u b sub sub 作为 1, 也会作为 C i − 1 C_{i-1} Ci−1 传进加法器中
- 对 Y 所有位按位取反再 +1, 即可完成 X-Y 到 X+(-Y) 的操作

7. 标志位生成
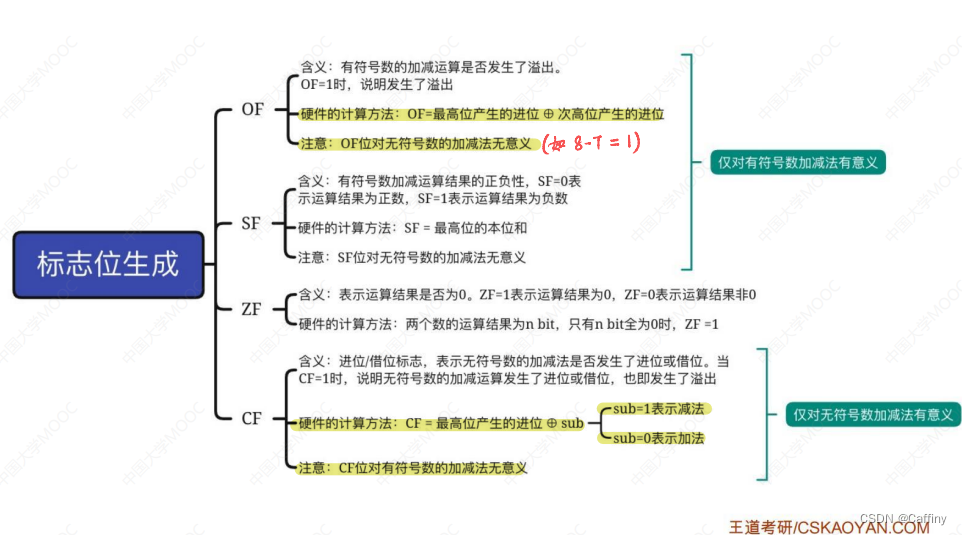
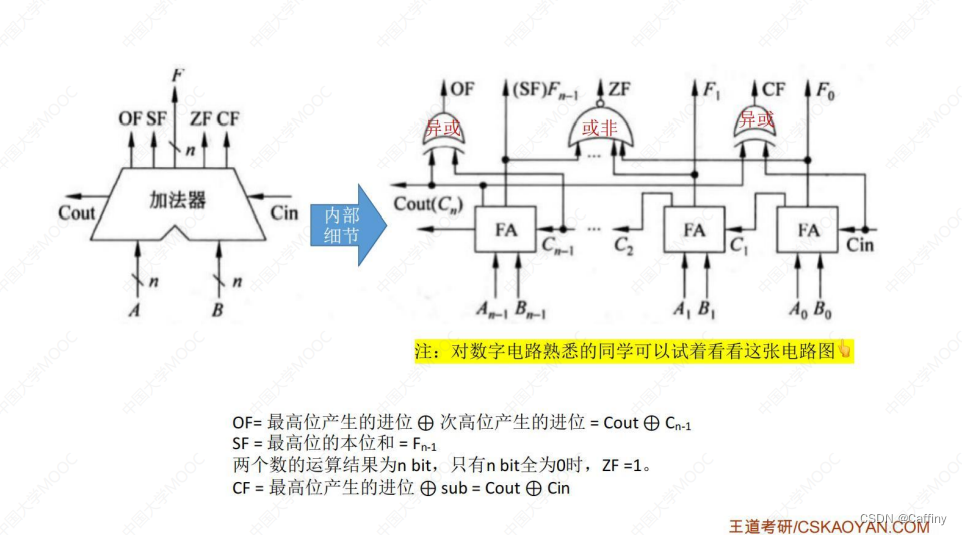
b. 定点数的移位运算
1. 算数移位

2. 逻辑移位
- 逻辑右移: 高位补0, 低位舍弃
- 逻辑左移: 低位补0, 高位舍弃
3. 循环移位
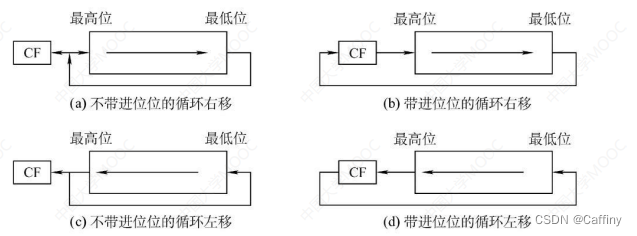
c. 定点小数的乘法运算
1. 原码乘法运算
- 符号位单独处理, 符号位 = x s ⊕ y s =x_s\oplus y_s =xs⊕ys
- 数值位取绝对值进行乘法运算:
- 先回顾几个运算器的构件:
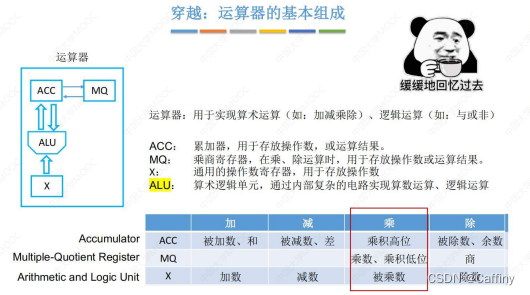
- 我们现在要计算: [ x ] 原 = 1.1101 , [ y ] 原 = 0.1011 , x ⋅ y [x]_原=1.1101, [y]_原=0.1011, x\cdot y [x]原=1.1101,[y]原=0.1011,x⋅y
- 先将被乘数, 即 x, 符号位变成 0, 取绝对值, 放进 通用寄存器 X X X 中
乘数, 即 y, 符号位也同样取 0, 取绝对值, 放进 乘商寄存器 M Q MQ MQ 中
累加器 A C C ACC ACC 全置 0;
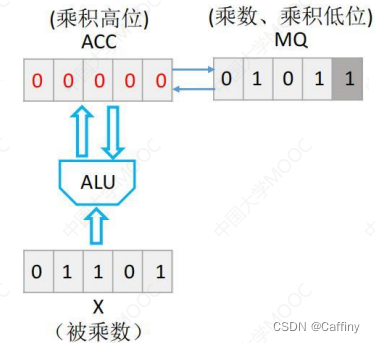
- 从右往左看 乘商寄存器 M Q MQ MQ, 第一个是 1 1 1
那么我们就往 累加器 A C C ACC ACC 里加上 通用寄存器 X X X 里的 被乘数 X X X
然后 累加器 A C C ACC ACC 和 乘商寄存器 M Q MQ MQ 一起 逻辑右移: 高位补 0 0 0, 低位舍弃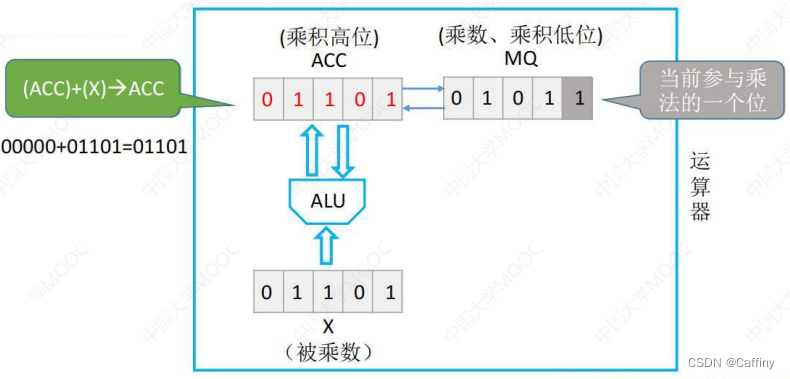
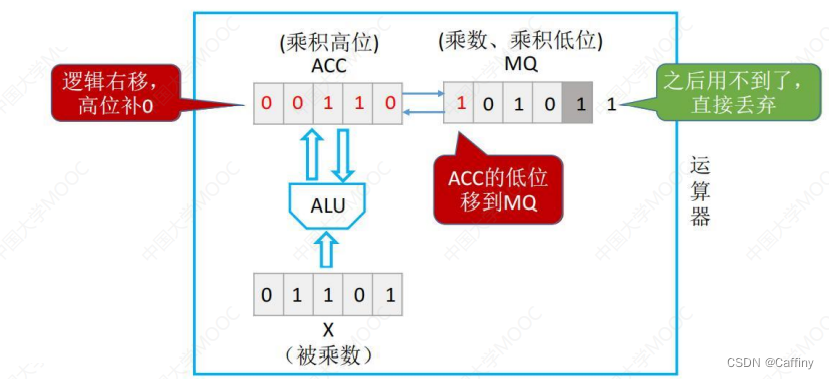
- 然后重复第四步, 还是 1 1 1, 于是我们对 累加器 A C C ACC ACC 先加 通用寄存器 X X X 里的被乘数, 然后 A C C ACC ACC 和 M Q MQ MQ 一起逻辑右移:
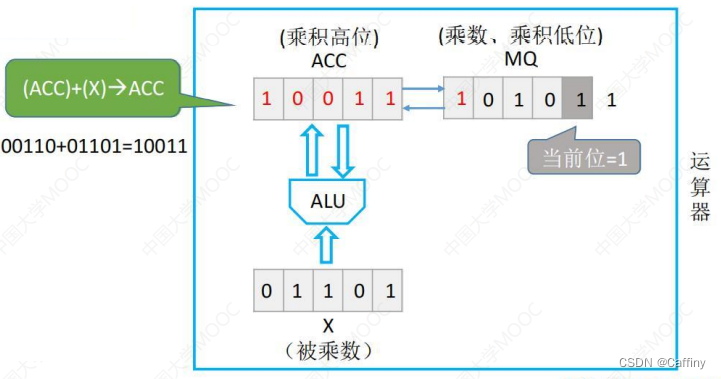
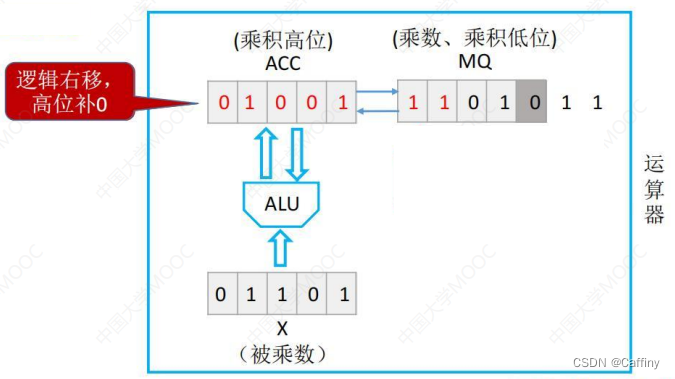
- 继续重复第四步, 但是这一次是 0 0 0, 如果遇到 0 0 0, 累加器 A C C ACC ACC 就什么都不加, 直接和 乘商寄存器 M Q MQ MQ 逻辑右移
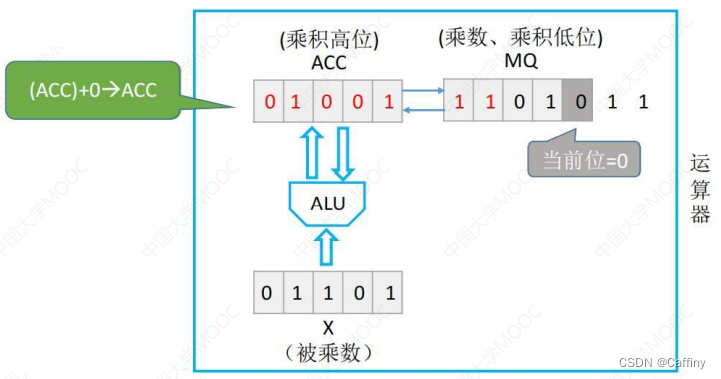

- 一直重复第四步, 直到原本放 乘数 的 乘商寄存器 M Q MQ MQ 里的符号位移到最后一个位, 就可以停止了
这个时候, 还需要把 累加器 A C C ACC ACC 的第一位, 即符号位修改为一开始的 符号位 = x s ⊕ y s =x_s\oplus y_s =xs⊕ys
然后 累加器 A C C ACC ACC 和 乘商寄存器 M Q MQ MQ 组合起来的数字就是最终乘积的结果
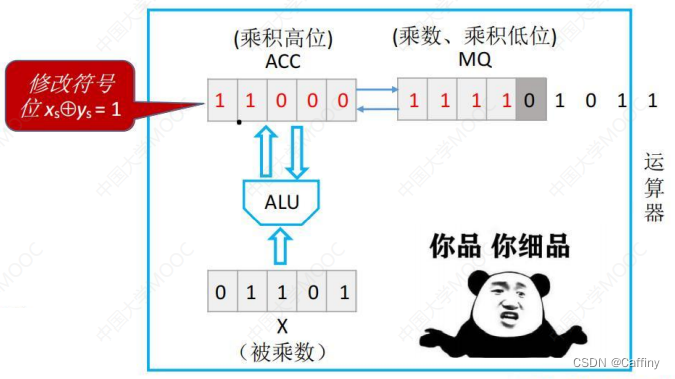
- 将上述过程简化成手算过程就是这样:

2. 补码乘法运算
- 补码乘法 和 原码乘法 类似, 但也有不同:
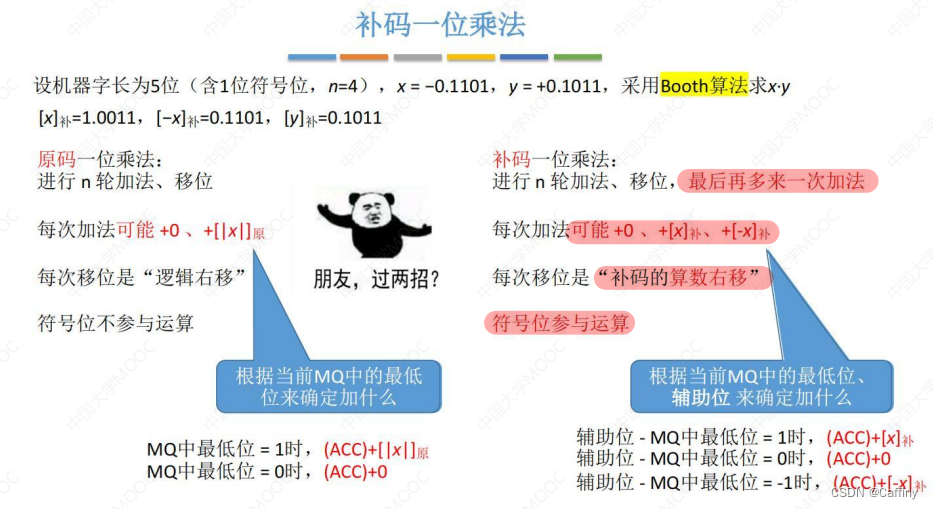
- 在 补码乘法 的运算中:
- 所有寄存器的机器字长统一 n + 2 n+2 n+2 位, 采用双符号位表示补码.
- 乘商寄存器 M Q MQ MQ 中, 用 单符号位表示 乘数 补码, 最后一位 机器位 放辅助位, 初始为0
- 辅助位 - M Q MQ MQ中最低位 = 1, ( A C C ) + [ x ] 补 (ACC)+[x]_补 (ACC)+[x]补
辅助位 - M Q MQ MQ中最低位 = 0, ( A C C ) + 0 (ACC)+0 (ACC)+0
辅助位 - M Q MQ MQ中最低位 = -1, ( A C C ) + [ − x ] 补 (ACC)+[-x]_补 (ACC)+[−x]补 - 加法结束后, A C C ACC ACC 和 M Q MQ MQ 一起 算数右移
- 一直右移到 原来放在乘商寄存器 M Q MQ MQ的乘数的符号位 后, 还得继续进行一次加法
- 最后 累加器 A C C ACC ACC 和 乘商寄存器 M Q MQ MQ 共同构成最后的乘积(带符号位)

d. 定点小数的除法运算
1. 原码除法运算
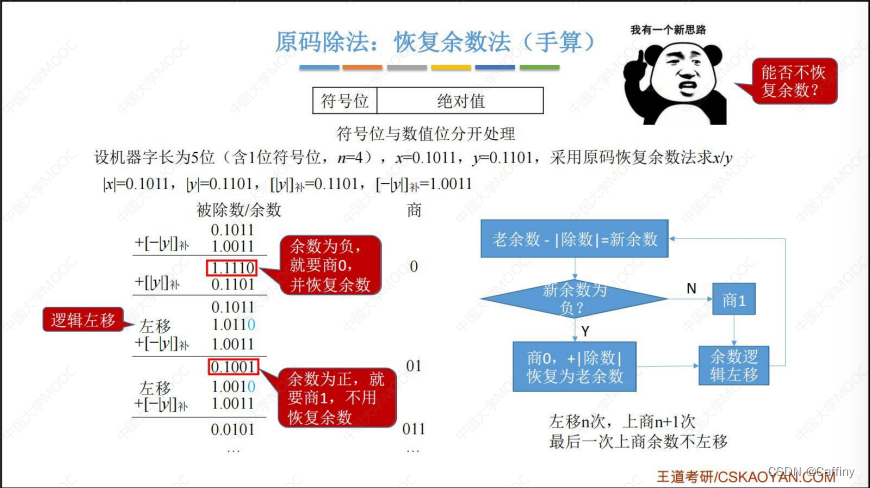
1-1. 恢复余数法
- 通用寄存器 X X X 存放 除数
累加器 A C C ACC ACC 存放 被除数
乘商寄存器 M Q MQ MQ 存放 结果商 - 符号位单独处理 x s ⊕ y s x_s \oplus y_s xs⊕ys
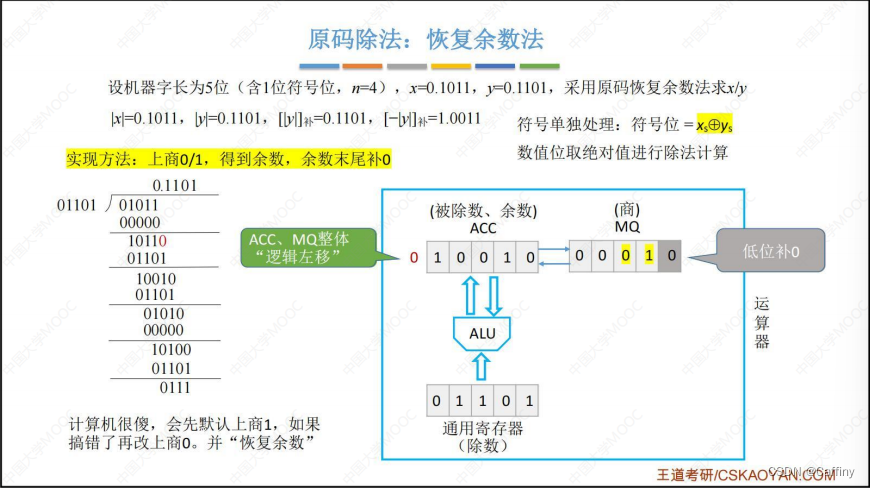
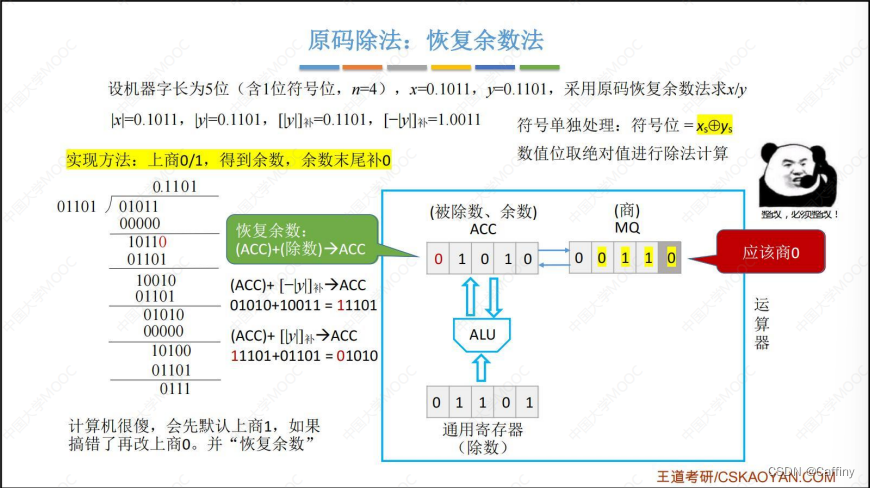
- 将对应 除数, 被除数 放入 通用寄存器 X X X, 累加器 A C C ACC ACC 中, 乘商寄存器 M Q MQ MQ置0
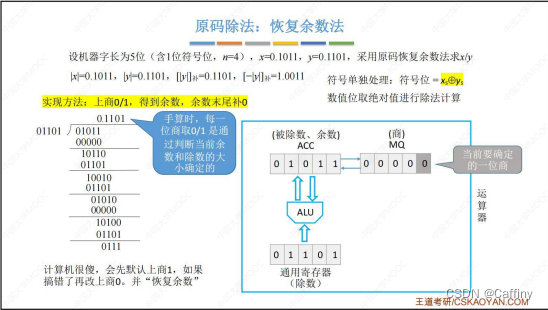
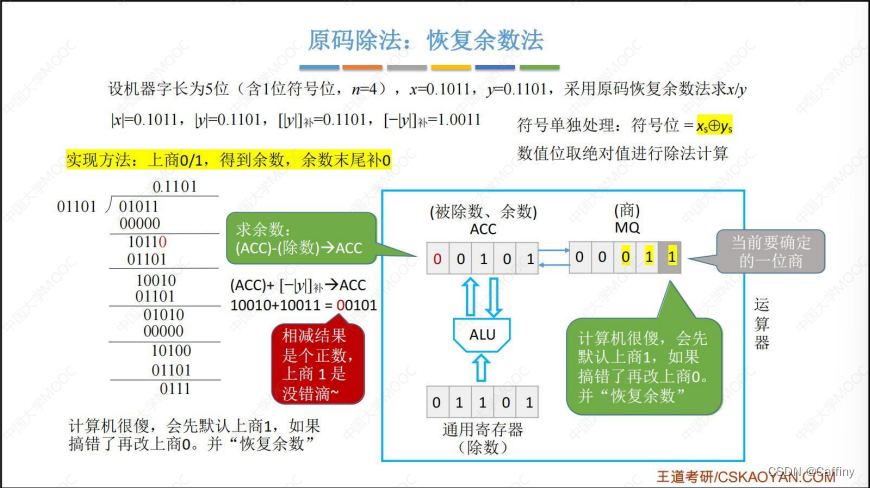
- 每轮直接无脑上商 1 1 1
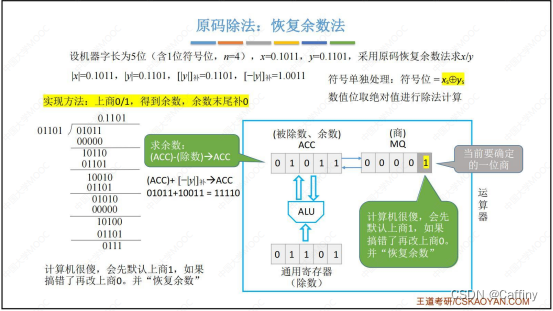
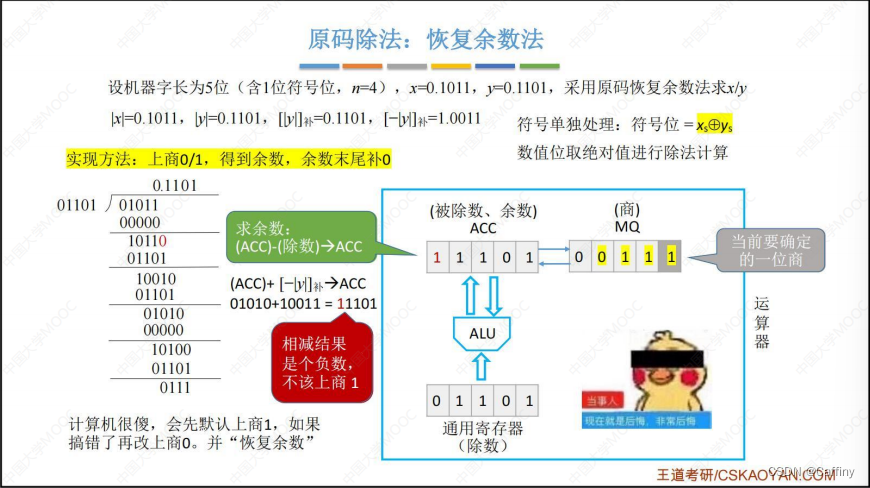
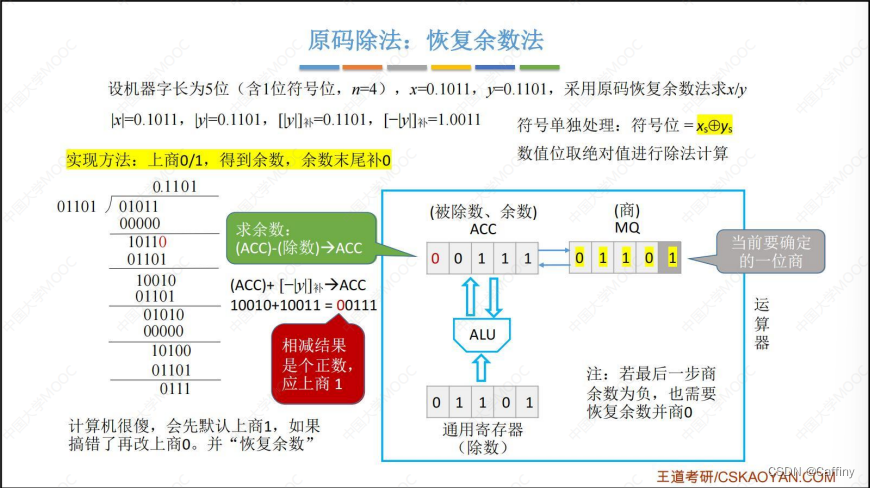
- 求余数: ( A C C ) − ( 除 数 ) → A C C (ACC)-(除数)\rightarrow ACC (ACC)−(除数)→ACC
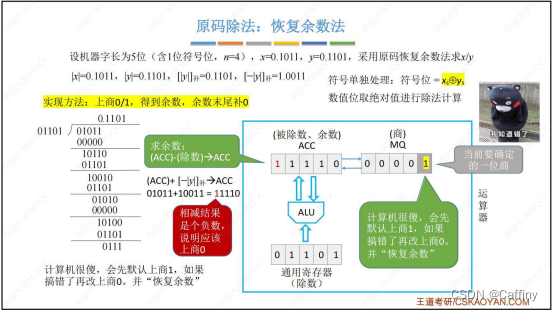
- 发现 A C C ACC ACC 中, 余数为负数, 商改为 0 0 0
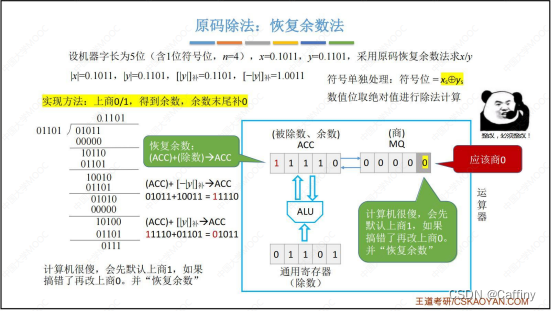
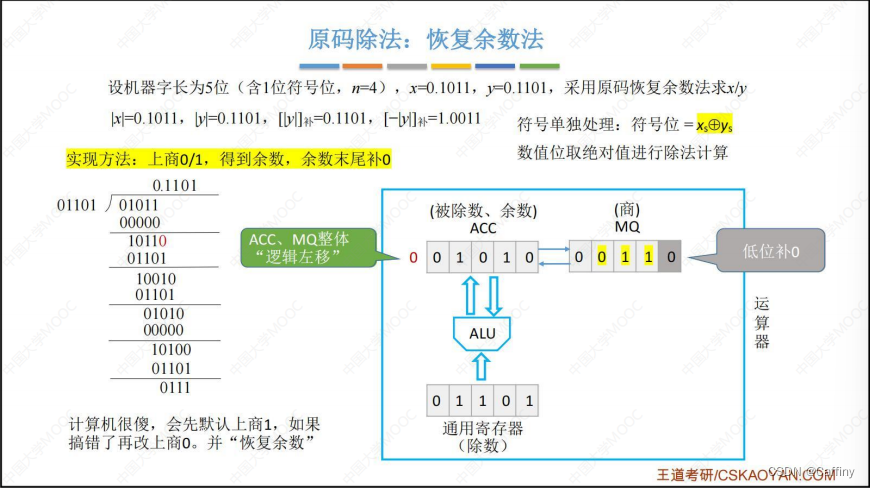
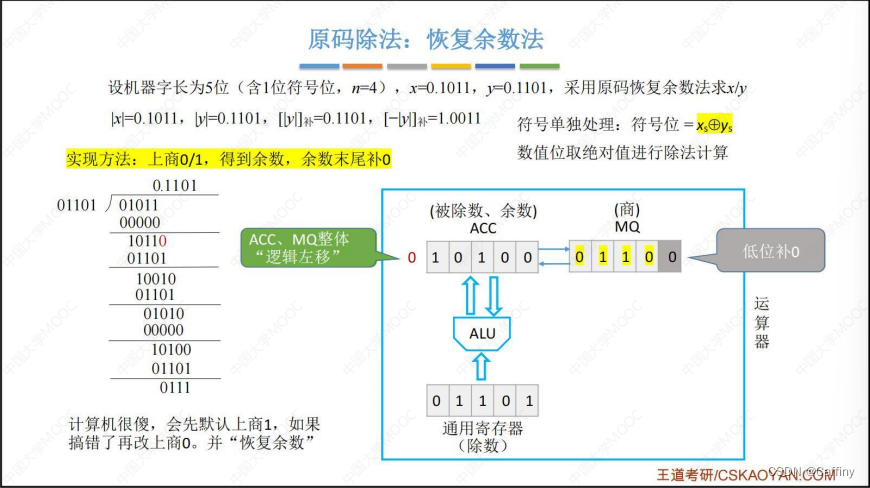
- 商改为 0 0 0 后, A C C ACC ACC 也应该改回来, 所以 ( A C C ) + ( 除 数 ) → A C C (ACC)+(除数)\rightarrow ACC (ACC)+(除数)→ACC, 这一步就叫 恢复余数
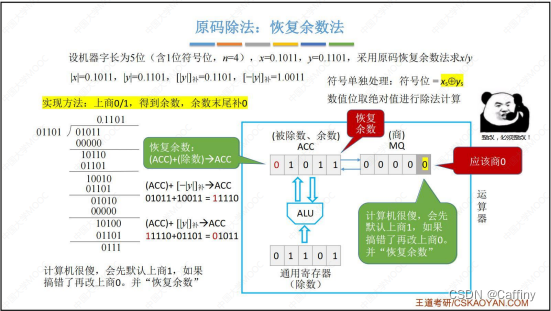
- 然后 A C C ACC ACC 和 M Q MQ MQ 总体 逻辑左移
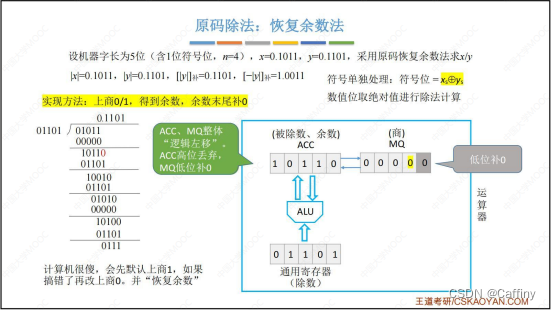
- 重复 1~5 步, 直至 乘商寄存器 M Q MQ MQ 中所有机器位的都有确定的商
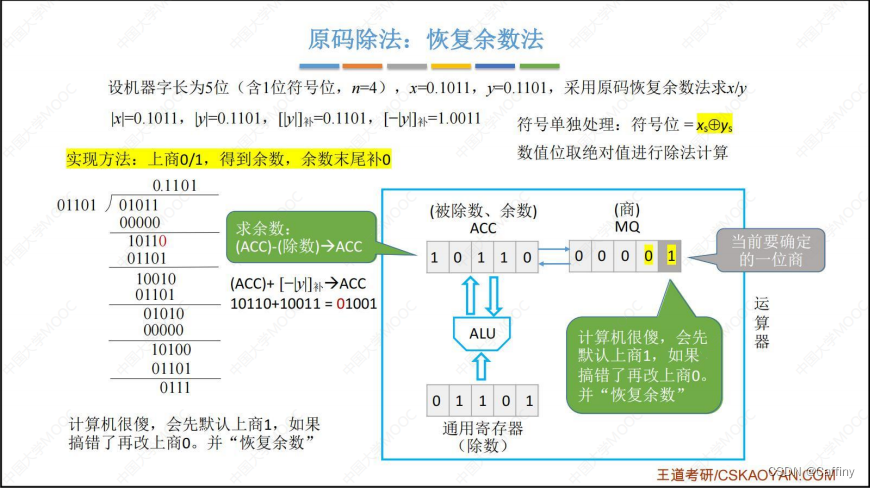
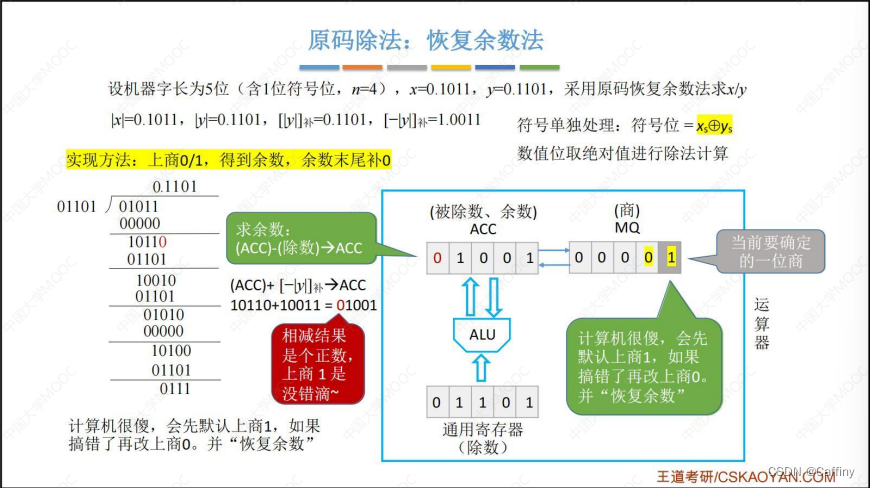
- 最后得到结果
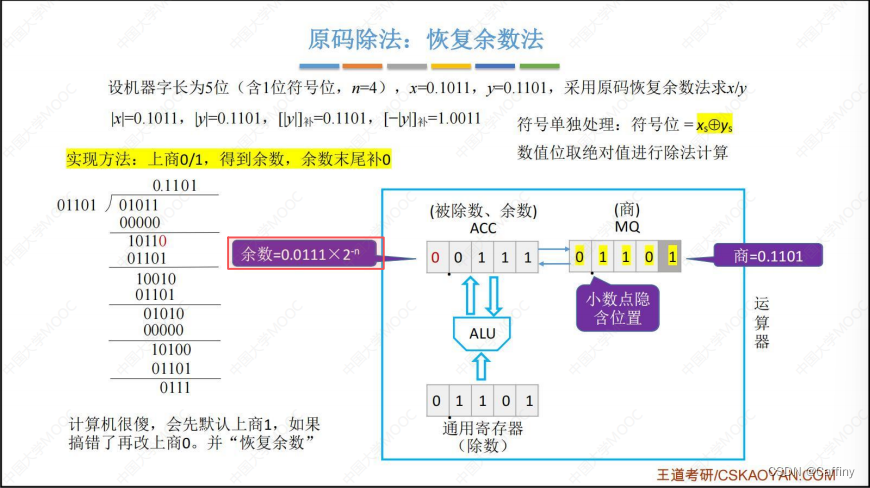
- 总结: 看流程图
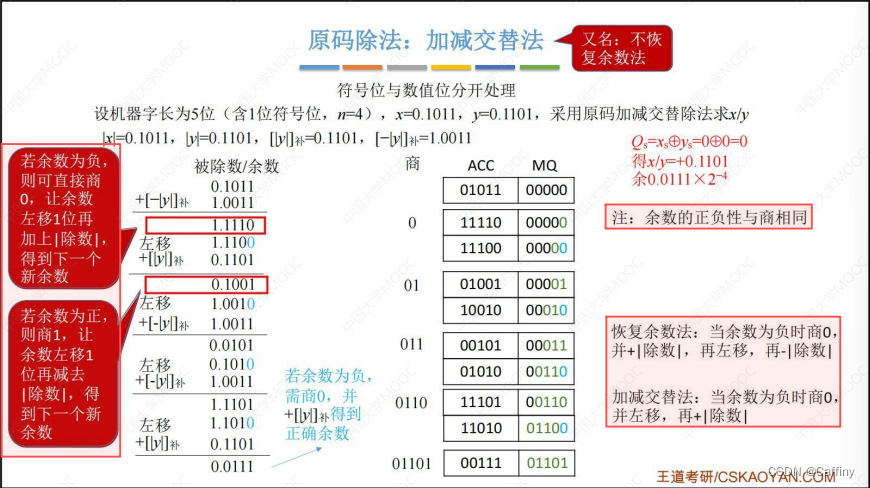
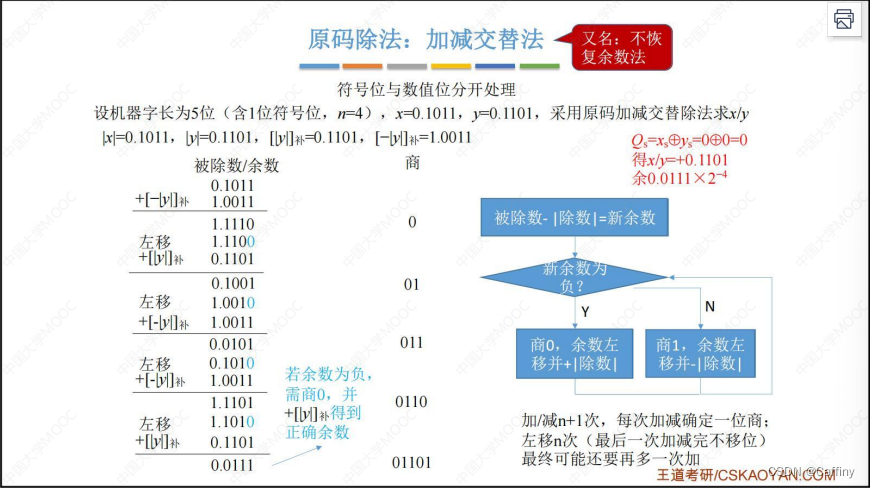
1-2. 加减交替法(不恢复余数法)
- 核心思想:

- 总体流程:
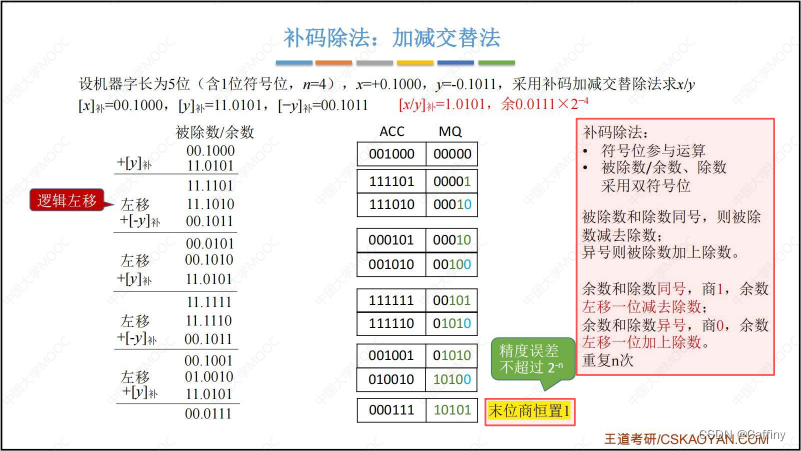
2. 补码除法运算
- 精髓:
- 有一道经典的题:

- 这道题如果不深究, 可以直接选 B B B, 应为补码的乘除法, 重点的一步就是 符号位 参与运算
- 如果深究的话:
- 什么叫够减: 被减数的 绝对值 大于 减数 绝对值
- 同号相除:
求余数 够减 商 不够减 商 减法 除数和余数同号 1 除数和余数异号 0 - 异号相处:
求余数 够减 商 不够减 商 加法 除数和余数异号 0 除数和余数同号 1 - 如: 被除数 -3, 除数 -2 和 +2, 够减
- − 3 与 − 2 同 号 ⇒ − 3 − ( − 2 ) = − 1 ⇒ 余 数 和 除 数 同 号 ⇒ 商 1 -3 与 -2 同号 \Rightarrow -3 - (-2) = -1 \Rightarrow 余数和除数同号 \Rightarrow 商1 −3与−2同号⇒−3−(−2)=−1⇒余数和除数同号⇒商1
- − 3 与 + 2 异 号 ⇒ − 3 + ( + 2 ) = − 1 ⇒ 余 数 和 除 数 异 号 ⇒ 商 0 -3 与 +2 异号 \Rightarrow -3+(+2)=-1 \Rightarrow 余数和除数异号 \Rightarrow 商0 −3与+2异号⇒−3+(+2)=−1⇒余数和除数异号⇒商0