介绍了三种方法,pixelRNN,VAE,GAN。笔记以VAE为主。
 pixelRNN比较容易理解,由已知推未知。
pixelRNN比较容易理解,由已知推未知。
这种方法还能应用到语音生成等领域

在这里有个tips值得说一下,图的每个像素一般RGB三色,问题出在当RGB三个值相差不大时最终的结果像素点的颜色趋向灰色,于是乎,为了使生成的图像更加鲜亮,就需要拉高三个值的差距。 简而言之,原本用三个数表示颜色 ,现在只用一个。

VAE是一个相对复杂的东西,事实上我看这个视频也是为了搞清它的工作原理。
VAE的整体架构是这样的,当训练结束后,把decoder单独摘出来,输入一组值得到生成的图像。
看起来VAE的应用蛮广泛的,比如生成诗句(其实称不上诗句,但原博客里这样写的)
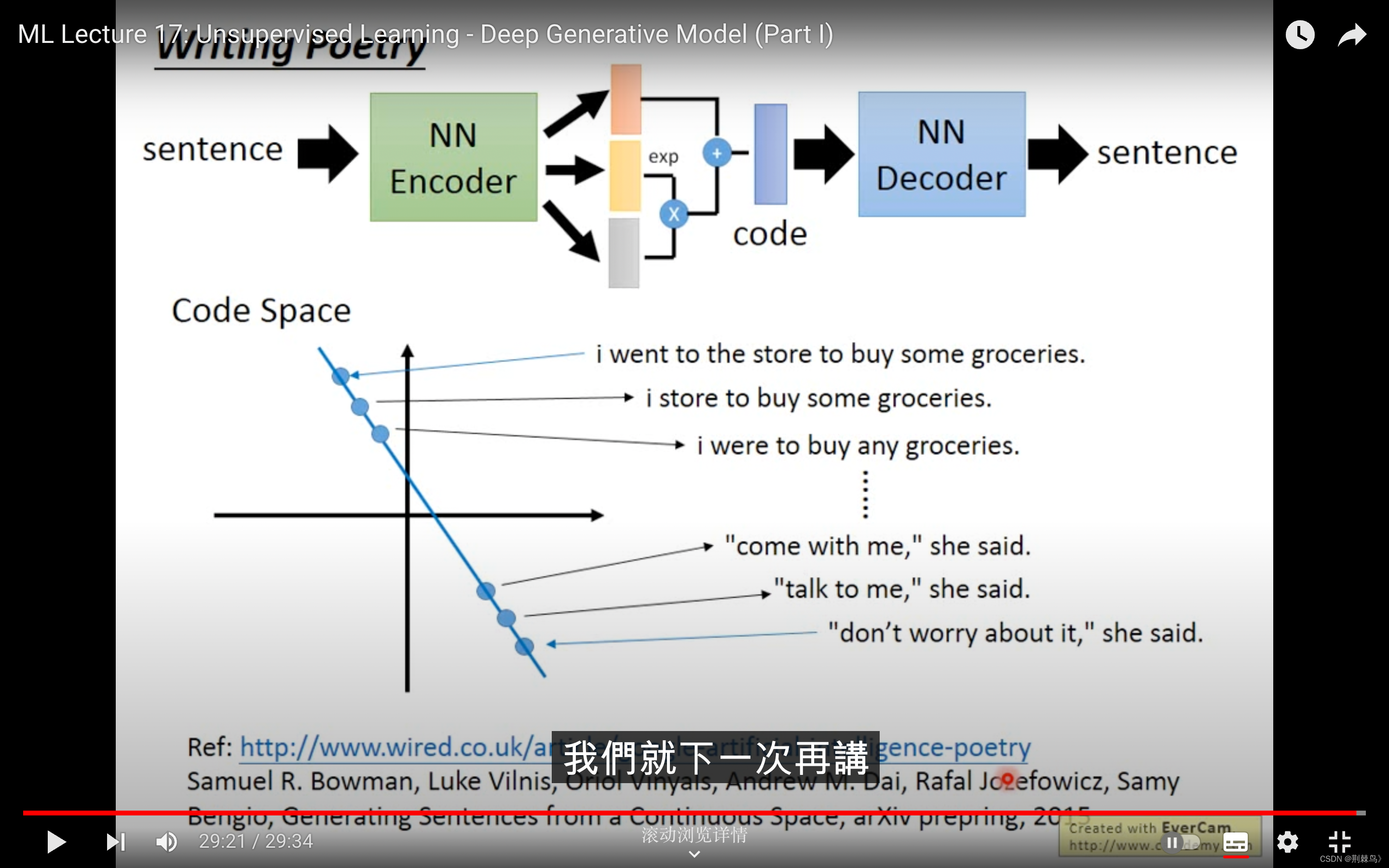
为什么不用AE非要使用VAE
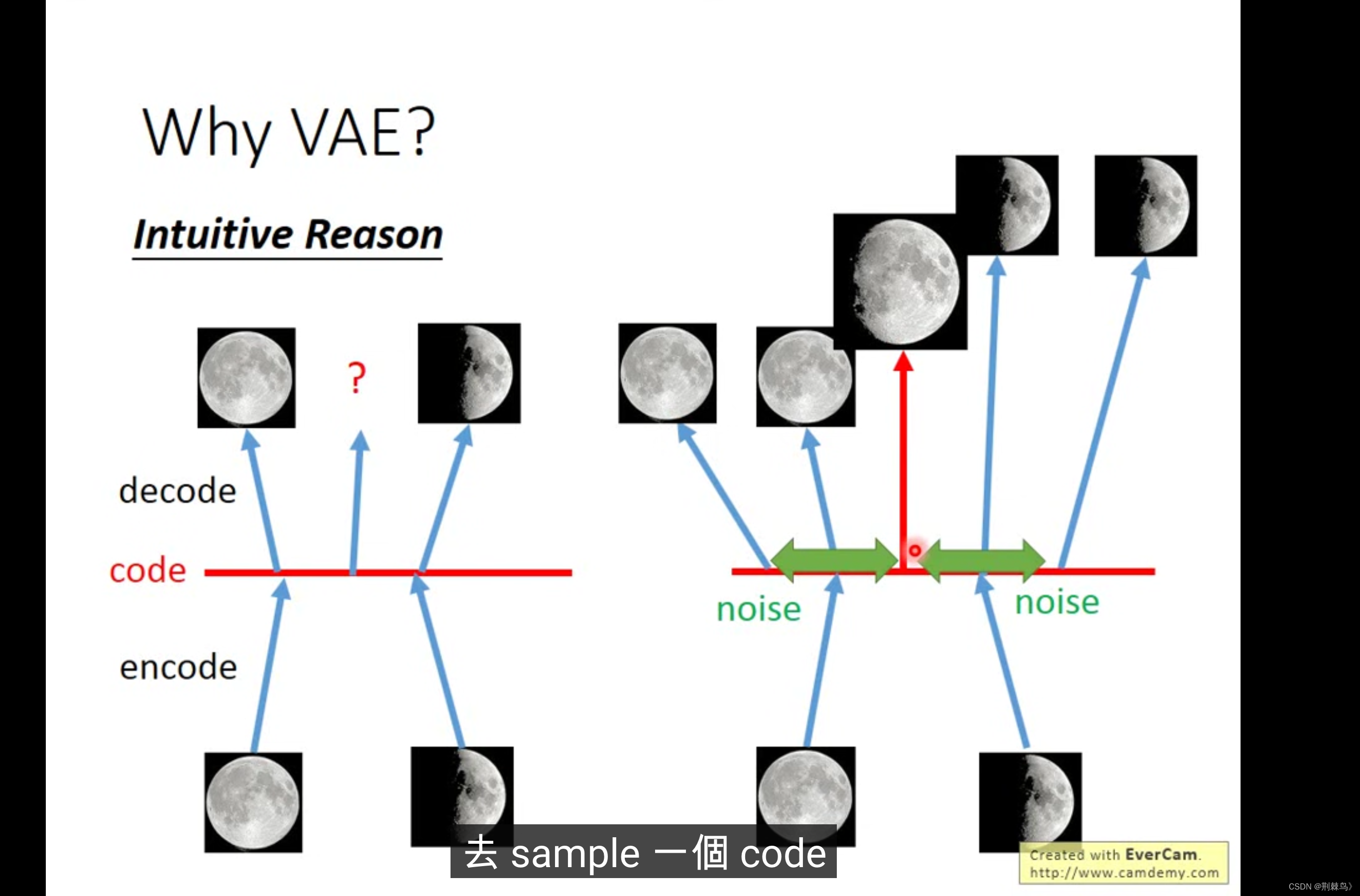
我们再次看到这张结构示意图
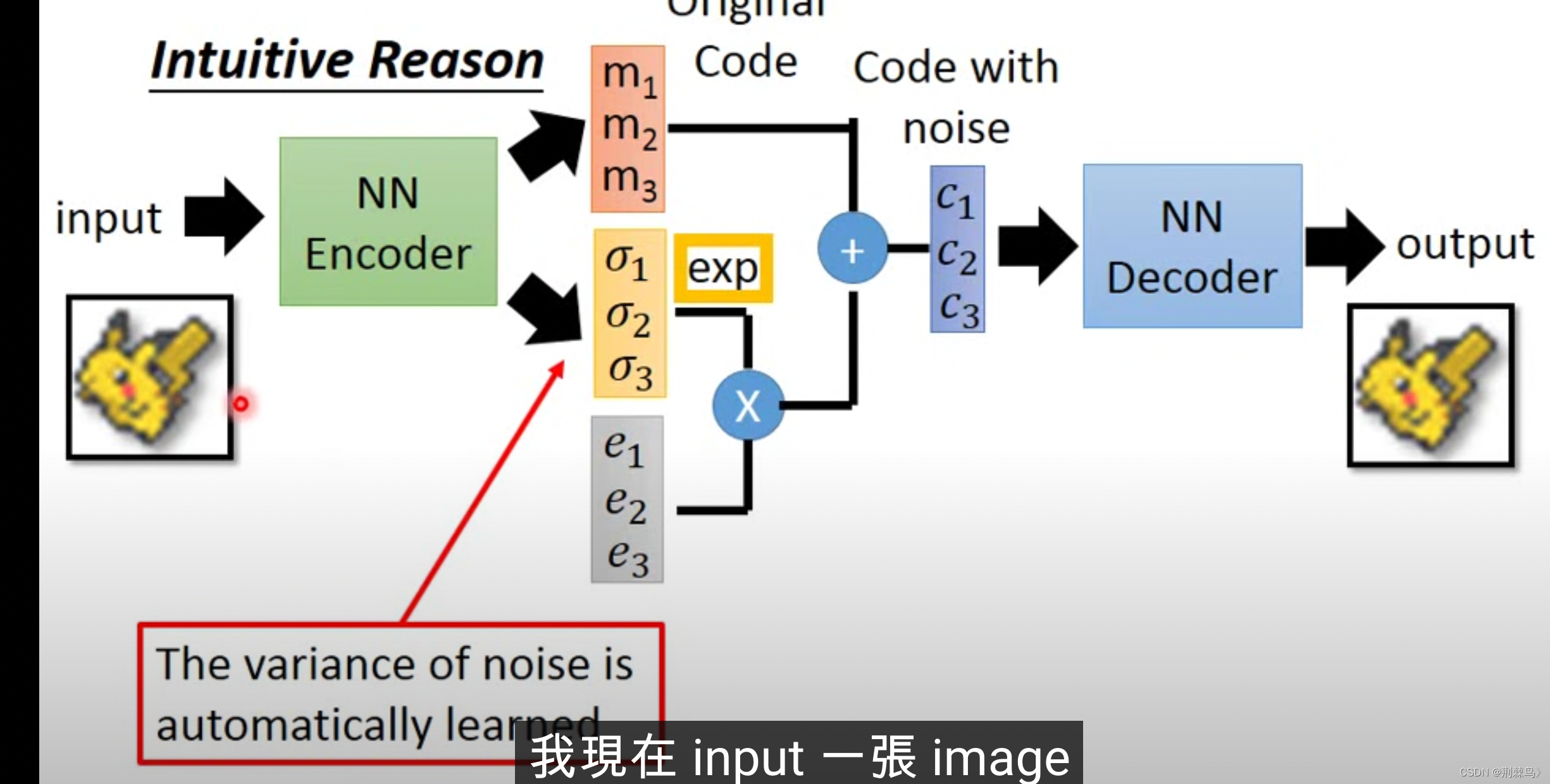
m看作μ,看作
,这两个参数是神经网络里的参数
VAE就是在AE中的基础上加了些扰动,比如e*
这样的话就会有所改变,但我们必须强迫该值不能太小,当
为0时,VAE就退化成了AE.

损失函数中增加一项,其值的含义是图中的绿色线条,当=0时损失该值最小
当=0时,
=1而非0
于是我们在这个基础上更加详细深入一点

我们现在要做的是估计P(x):即输入图像的概率分布(上图以一维为例)

上图其实是有许多个gaussion分布组合而成的。
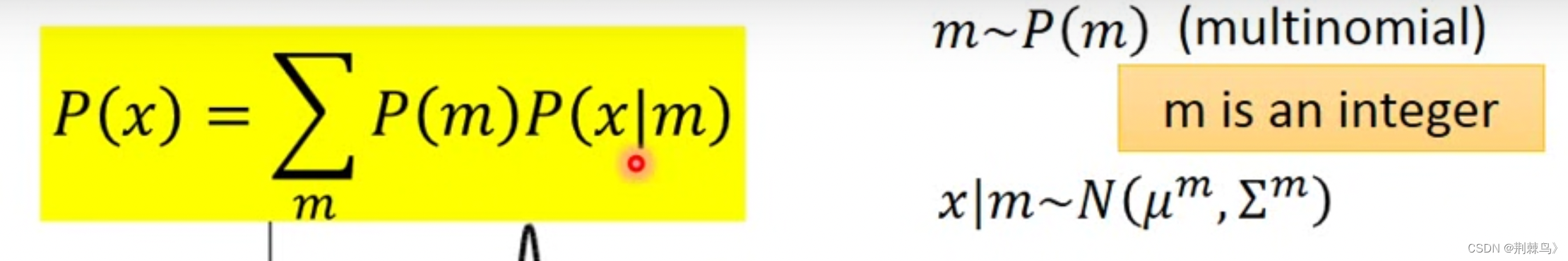
当要sample出来一个值时,这里面有许多个gaussion可供我们选择,每个gaussion拥有自己独有的权重(我更喜欢称之为与
),然后从选出的gaussion中sample出一个x
接下来就是重点中的重点——映射!!!
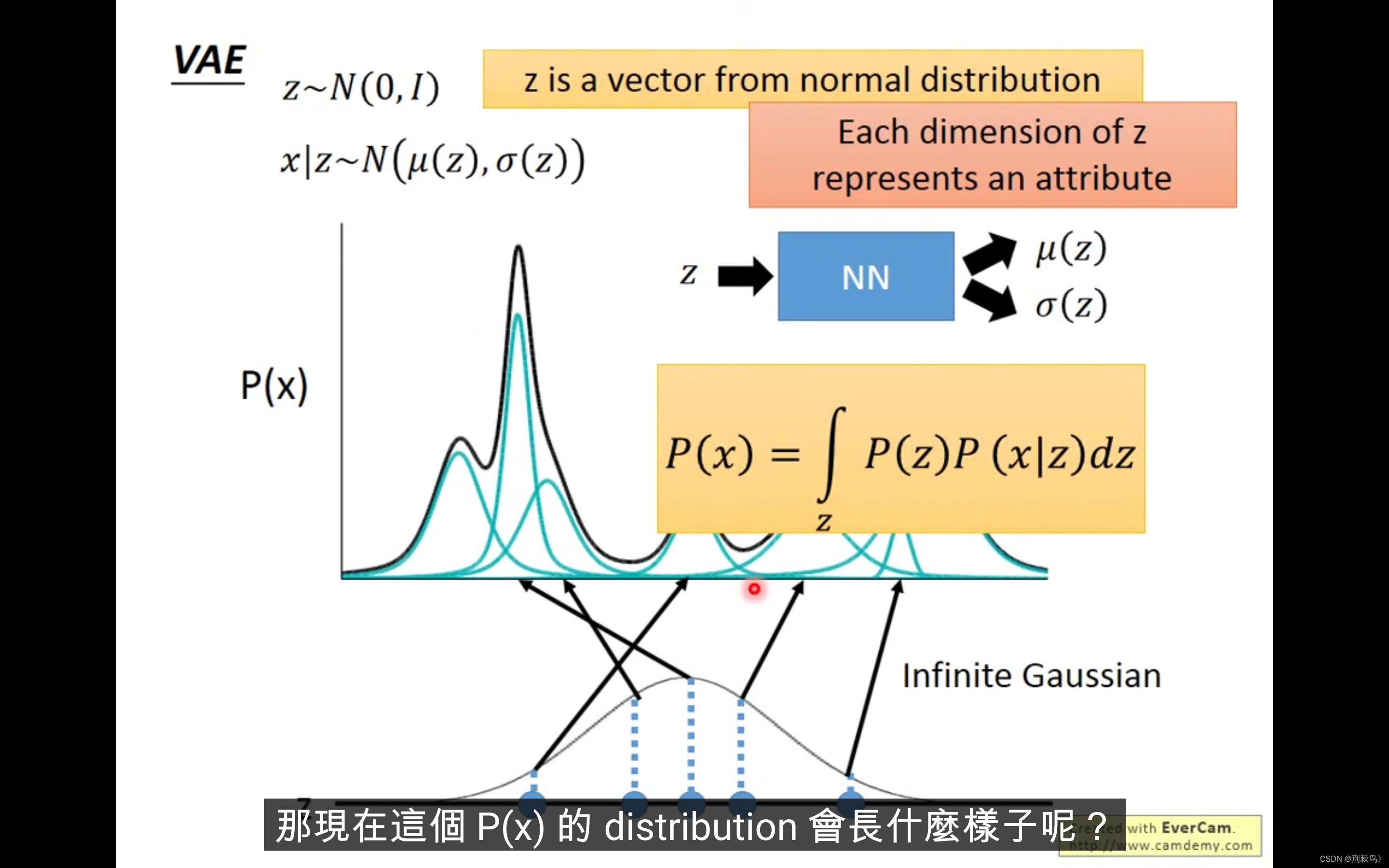
z服从正太分布(假定是一维的),那么z上每一个点都对应图中的一个gaussion分布
具体对应哪一个,看该函数——

说实话截止目前,我仍旧不懂这种映射关系,直到我看到了这个表达式——

总而言之,上图其实是有许多个gaussion分布组合而成的,比如有10个,那么能sample就最多有10种情况,但当我们采用映射的方法,z拥有无穷多的可能, 与
也就拥有无穷多种可能。
因此神经网络的目的就是找到一组权重使得——


如图所示,我们从寻找P(x|z)变成了寻找P(x|z)与q(z|x)
当我们通过改变q(z|x)来增加时,KL(q(z|x)||P(z|x))值将不断缩小(问为什么?Log(P(x))不会改变,
增加,kl自然减少)
当kl值不断减少,意味着 q(z|x)与P(z|x)越来越相近
继续分析的表达式

q是什么?
q(z|x)是任意一个分布,最小化kl值其实就是使q得分布和P(z)分布尽可能相近

插了个题外话AE的工作原理

GAN
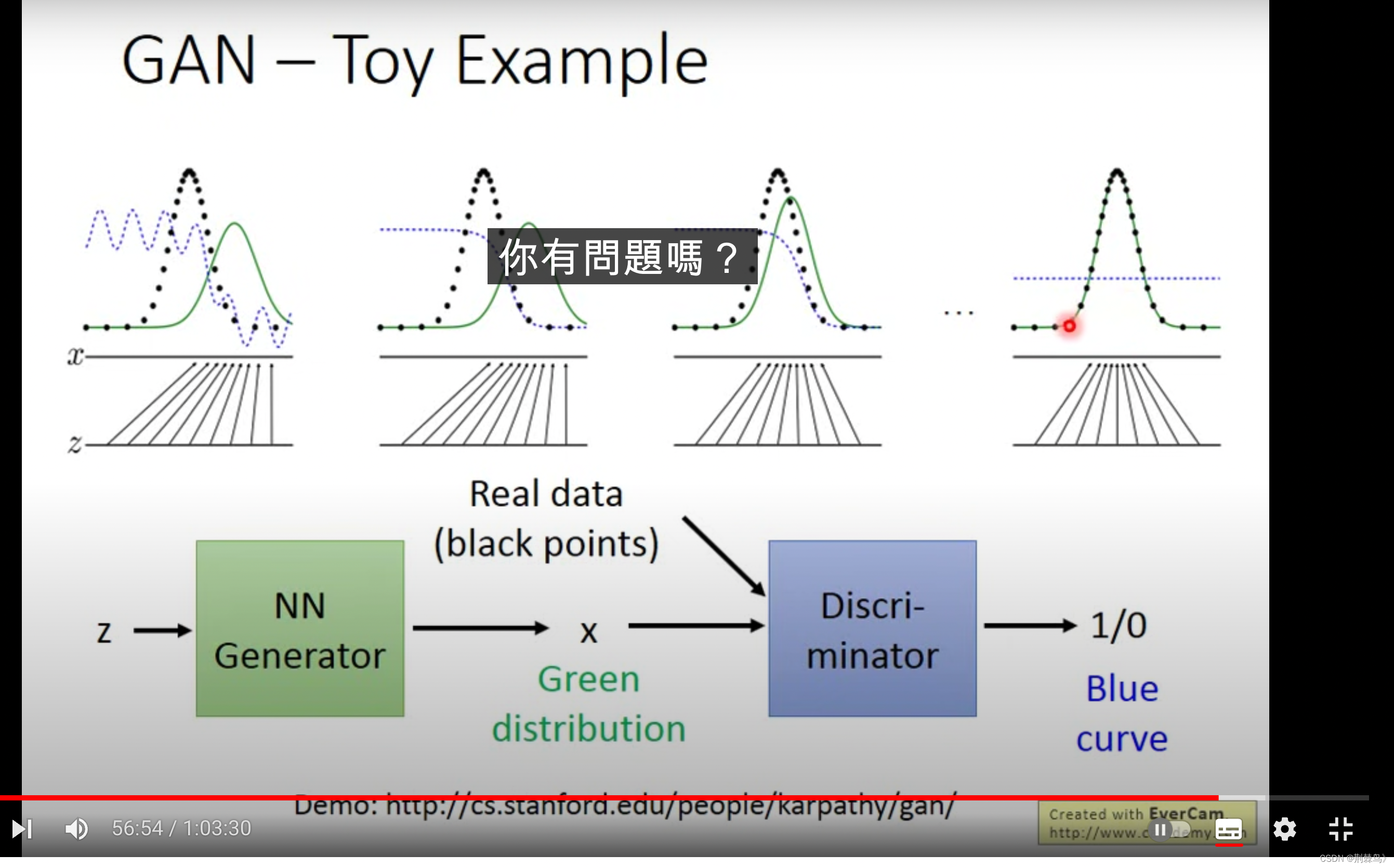
关于VAE的一些补充:
上述内容第一次很难看懂,花了半天时间找了找其他资料,恍然大悟,特此分享一下。
搞懂VAE的最好的出发点是为什么要用VAE替代AE
- X的维度较高,Z的维度也不可能很低,因此计算复杂度高。
- 对于某个实例 x 而言,与之强相关的 z 是相对有限的,为了找到这些有限的 z 可能需要大量的采样。

先看第二点,

如上图所示,当问题维度很大时,无法再保证采样变量zi与真实样本xi的一一对应关系,因此生成样本与真实样本之间也不再是一一对应关系,因此loss难以计算。
于是VAE做出了改变:把n个样本一起放进编码器中——>把样本一个一个放入编码器中。仅此而已。
下面这句是AE和VAE共通的地方:输入样本,输出的是样本映射的某种分布的均值与和log(
)
AE就直接输出均值,也就是z=,VAE的另一个改变是:z=
+

如何解决第一个问题?计算量大主要集中在pθ(z|x)
我们直接求pθ(z|x)十分复杂,但如何我们构造另一个分布,然后让这两个分布的距离越来越近,就迂回地解决了这个问题。
我们新建一个分布称为qϕ(z|x)
区分一下qϕ(z|x)、pθ(z|x)和pθ(z)的意义?
pθ(z):先验分布,z本身分布,一般认为是高斯分布
pθ(z|x):真实的后验分布(z|x),但较难求解
qϕ(z|x):编码器,不断地反向求导就是在使得qϕ(z|x)越来越逼近pθ(z|x),又因为我们一般假定pθ(z|x)是高斯分布,于是——不断地反向求导就是在使得qϕ(z|x)越来越逼近N(0,I)
如何使qϕ(z|x)越来越逼近N(0,I)?

上文提到的损失函数就是这样得到的

如上图所示,当μ=0,=
=1是,loss最小,也就是N(0,1)时损失为0
我对VAE是这么理解的,但貌似对其本质结构还不怎么了解,但通过这两天的学习对VAE有了一个及其粗糙的理解,后续可能会更改。
第二次更新,二刷李宏毅老师对VAE损失函数的讲解,又有感触。
我们的目的是最大化
通过化简,我们将其分成两部分:与KL散度
可以通过改变P(z|x)来最大化
,但这样存在一个问题:
确实增加了,但KL散度可能会降低,也就是说
可能会不增反降
为此,特地引入P(z|x)与q(z|x)来共同增加,这样做有若干好处:q(z|x)不断迫近P(z|x),kl散度不断降低,当最优情况kl散度降至0时,
增加时,
一定同时增加
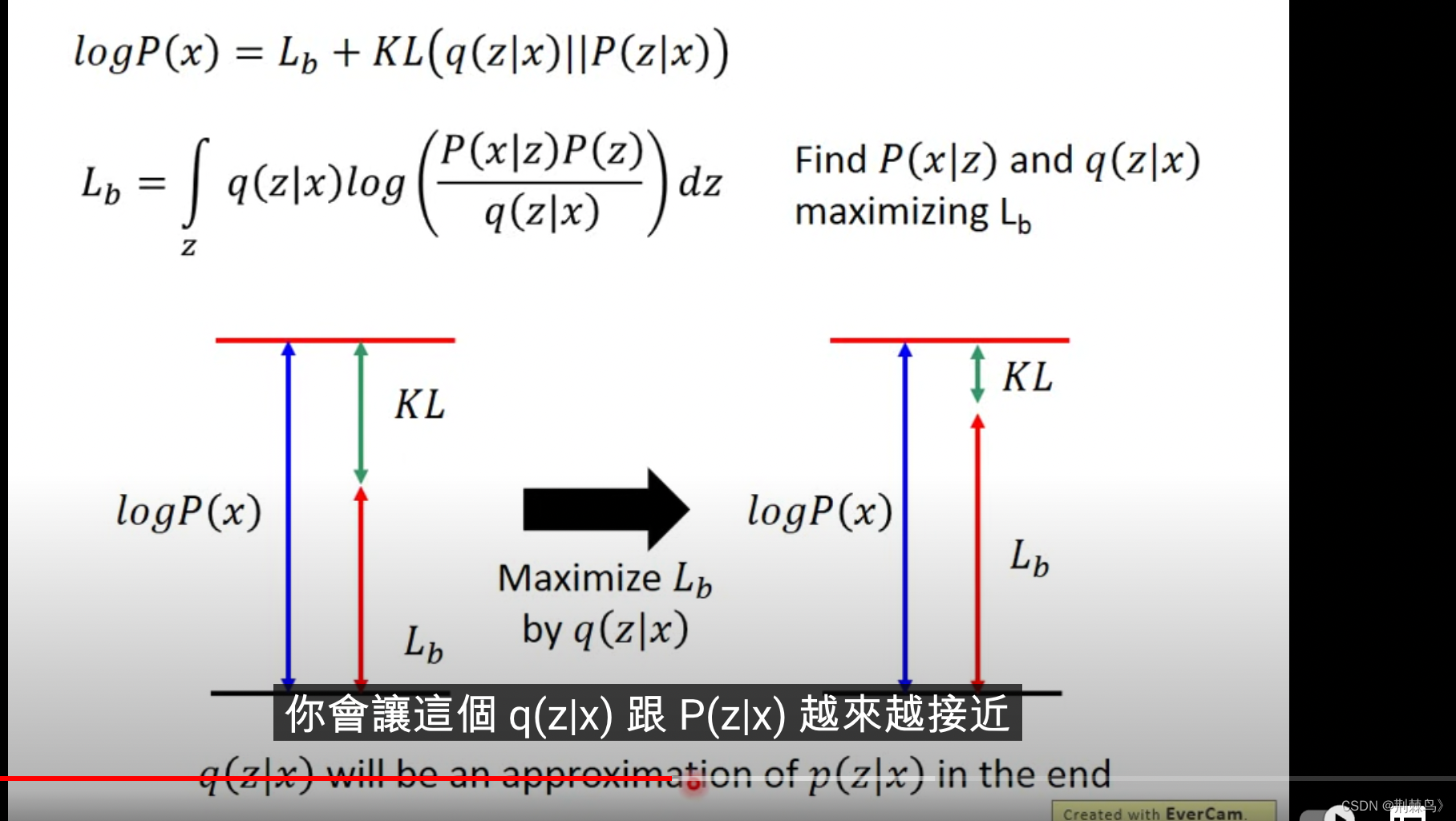
接下来谈谈如何改变P(z|x)与q(z|x)来增加
最小化kl散度(与上面提到的不是一个),本质是q(z|x)不断逼近正太分布N(0,1),这部分经过复杂的与运算可以转化为我们常见的形式(黄框内容)
第二部分是要增大的,其实也是最核心的内容,生成的不断逼近x
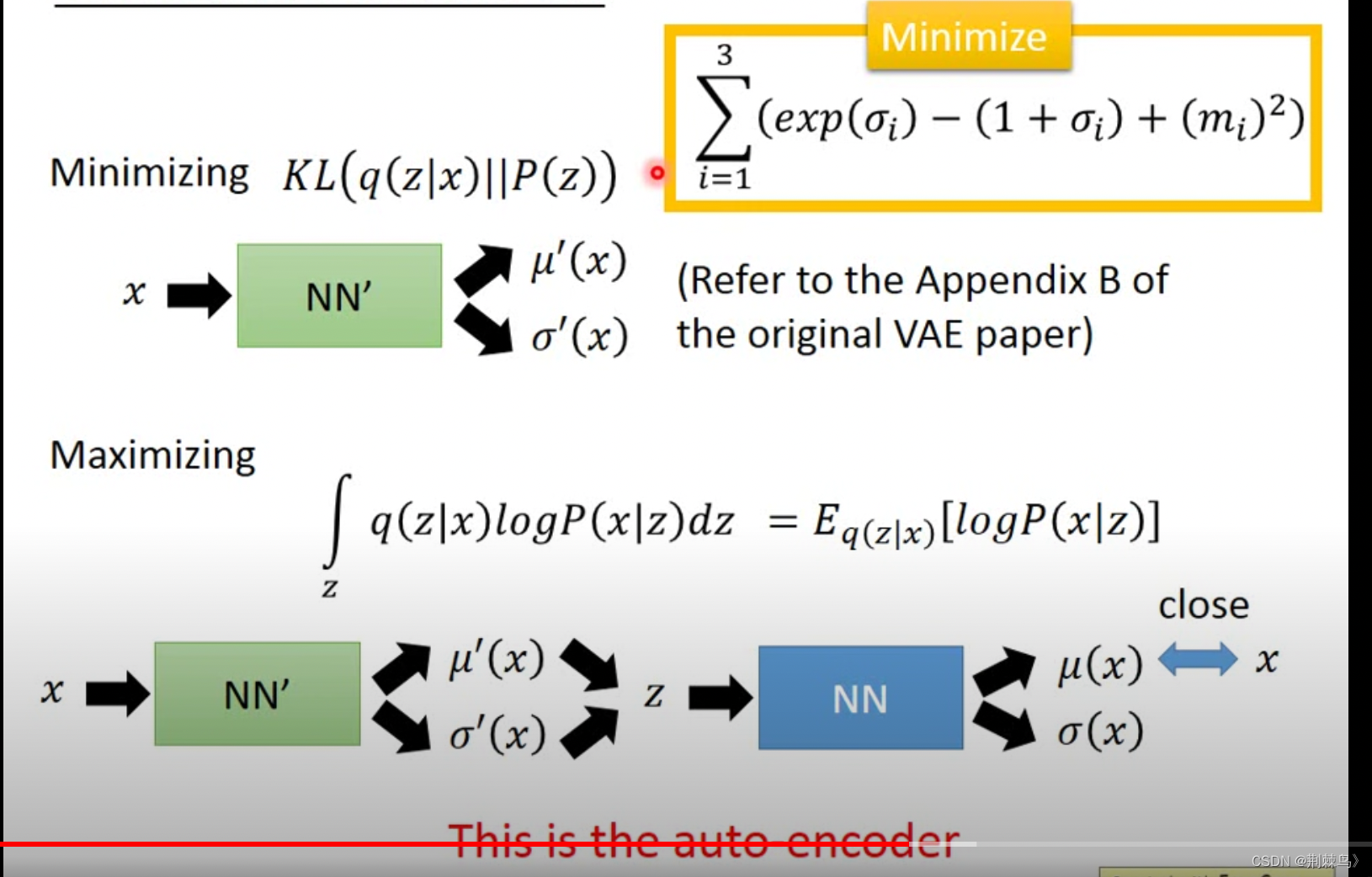
换句话,VAE的损失函数主要包括两部分:
第一,编码器q(z|x)应该越来越逼近N(0,1)
第二,重构x与样本x的差距损失