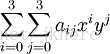//! interpolation algorithm
enum
{
INTER_NEAREST=CV_INTER_NN, //!< nearest neighbor interpolation
INTER_LINEAR=CV_INTER_LINEAR, //!< bilinear interpolation
INTER_CUBIC=CV_INTER_CUBIC, //!< bicubic interpolation
INTER_AREA=CV_INTER_AREA, //!< area-based (or super) interpolation
INTER_LANCZOS4=CV_INTER_LANCZOS4, //!< Lanczos interpolation over 8x8 neighborhood
INTER_MAX=7,
WARP_INVERSE_MAP=CV_WARP_INVERSE_MAP
};
//! resizes the image
CV_EXPORTS_W void resize( InputArray src, OutputArray dst,
Size dsize, double fx=0, double fy=0,
int interpolation=INTER_LINEAR );
//! warps the image using affine transformation
CV_EXPORTS_W void warpAffine( InputArray src, OutputArray dst,
InputArray M, Size dsize,
int flags=INTER_LINEAR,
int borderMode=BORDER_CONSTANT,
const Scalar& borderValue=Scalar());
//! warps the image using perspective transformation
CV_EXPORTS_W void warpPerspective( InputArray src, OutputArray dst,
InputArray M, Size dsize,
int flags=INTER_LINEAR,
int borderMode=BORDER_CONSTANT,
const Scalar& borderValue=Scalar());
(2)imgwarp.cpp中有插值函数,resize
(3) float a=1.0f在内存中的表示是3f800000,这个3f800000是怎么得出的?3f800000H=0 01111111 00000000000000000000000B (注意我分成了三段)
符点型数据在X86机上占四个字节,其存储按IEEE754标准实现,即:
1位的符号位s 0(代表正数,1代表负数)
8位的指数位e(移码表示)01111111是0的移码
23位的小数位f 0000000000000000000000 表示小数部分为0
计算机在表示符点数时,要将10进制数转成二进制的规范数形式进行存储的。即:1.f*2^e在存储时,小数前面的1是隐式存储的,不体现在数据中。
现在翻译一下:
3f800000H=1.0*2^0=1.0
(4)移码
符号位 阶码 尾数
浮点数的运算规则
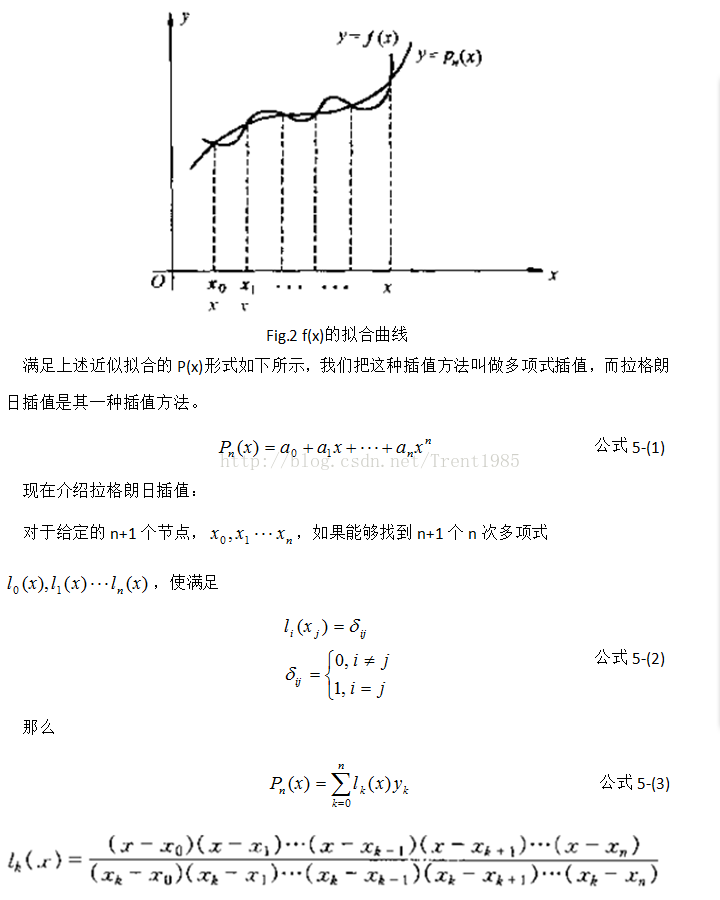
(1)最近邻插值
1 最近领内插值算法
就是令变换后像素的灰度值等于距它最近的输入像素的灰度值
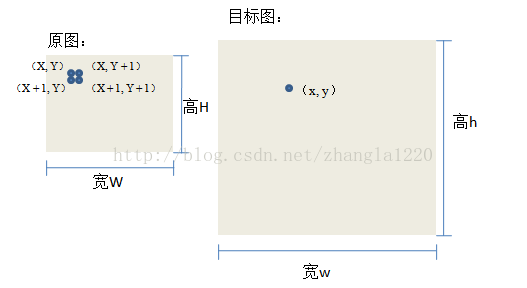
如上图 按照比例一致 可知道
Y = W / w * y;
X = H / h * x;
则目标图(x, y)处的灰度值与原图(X, Y )处的灰度值一致: f(x, y) = f(X, Y)
2 双线性插值
在x y两个方向上分别进行一次线性插值,方向先后不影响顺序。
如上图所示
目标图(x, y) 映射到原图是(X + u, Y + v)(计算方法同最邻近插值)。设u与v分别为X + u,Y + v的小数部分。
由于下标都是整数,因此原图其实并不存在该点。
则取其附近四个领域点为(X, Y) (X, Y + 1) (X + 1, Y) (X + 1, Y + 1)
则目标图(x, y)处的值为 f(x , y) = f(X + u, Y + v) =f (X, Y) * (1 - u) * (1 - v) + f(X, Y + 1) * (1 - u) * v + f(X + 1, Y) * u * (1 - v) + f (X + 1, Y + 1) * u * v;
(6)
目前比较常用的插值算法有这么几种:最邻近插值,双线性二次插值,三次插值,Lanczos插值等等,
1,最邻近插值
最邻近插值算法也叫做零阶插值算法,主要原理是让输出像素的像素值等于邻域内
离它距离最近的像素值。例如下图中所示,P1距离0灰度值像素的距离小于100灰度值的
距离,因此,P1位置的插值像素为0。这个算法的优点是计算简单方便,缺点是图像容
易出现锯齿。
2,双线性二次插值
在介绍双线性插值前,我们先介绍一下拉格朗日插值多项式。本文参考引用均来自
张铁的《数值分析》一书。
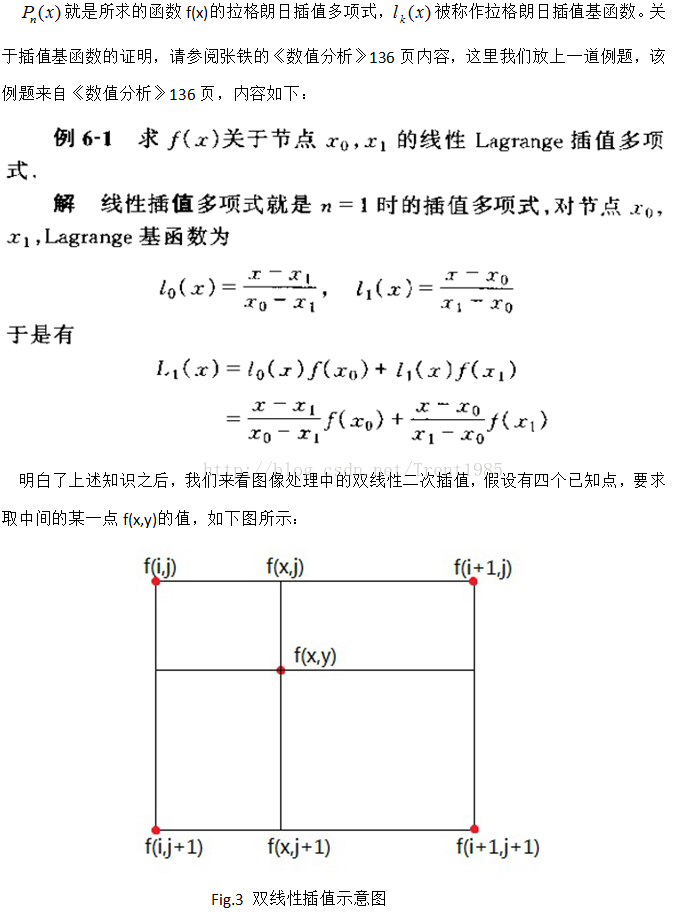
我们的方法是这样的,根据水平方向上的双线性二次插值,由f(I,j)和f(i+1,j)求取f(x,j),由
f(I,j+1)和f(i+1,j+1)求取f(x,j+1),然后再根据这两点的二次插值求取f(x,y)。
根据前面的例题,我们可以很容易的求取各点插值如下:
f(x,j)=(i+1-x)f(I,j)+(x-i)f(i+1,j) 公式1-(4)
f(x,j+1)=(i+1-x)f(I,j+1)+(x-i)f(i+1,j+1) 公式1-(5)
f(x,y)=(i+1-y)f(x,j)+(y-j)f(x,j+1) 公式1-(6)
以上三式综合可以得到:
f(x,y)=(j+1-y)(i+1-x)f(I,j)+(j+1-y)(x-i)f(i+1,j)+(y-j)(i+1-x)f(I,j+1)+(y-j)(x-i)f(i+1,j+1) 公式1-(7)
我们令x=i+p,y=j+q得:
f(i+p,j+q)=(1-q)(1-p)f(I,j)+p(1-q)f(i+1,j)+q(1-p)f(I,j+1)+pqf(i+1,j+1) 公式1-(8)
上式即为数字图像处理中的双线性二次插值公式。
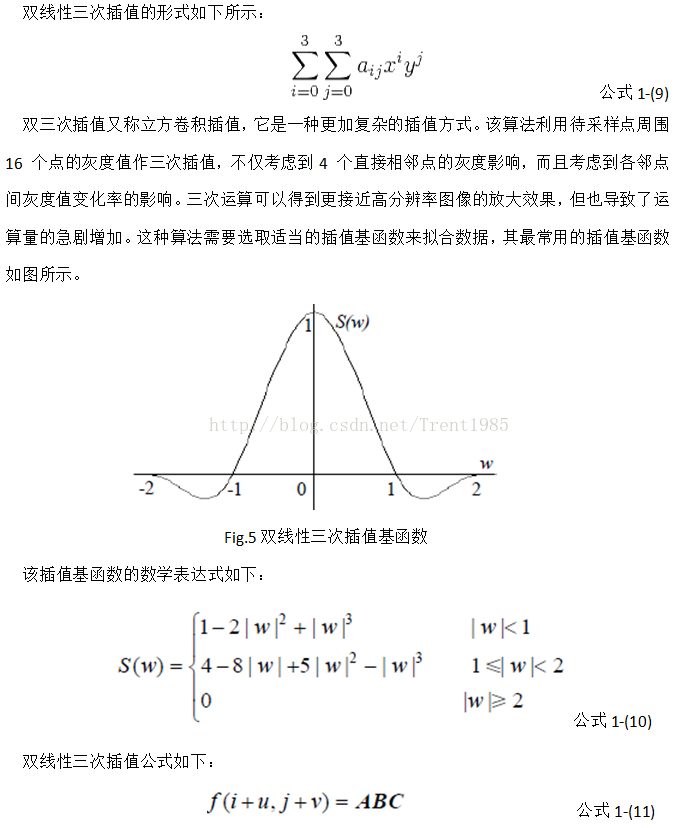
3,双线性三次插值
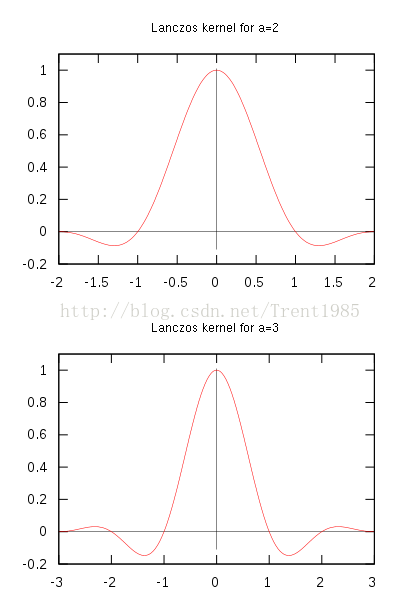
4,Lanczos插值算法
该算法的主要原理介绍地址:http://en.wikipedia.org/wiki/Lanczos_resampling
这里我大概介绍一下算法的流程:
这个算法也是一个模板算法,主要内容是计算模板中的权重信息。
对于一维信息,假如我们输入点集为X,那么,Lanczos对应有个窗口模板Window,这个窗口中每个位置的权重计算如下:
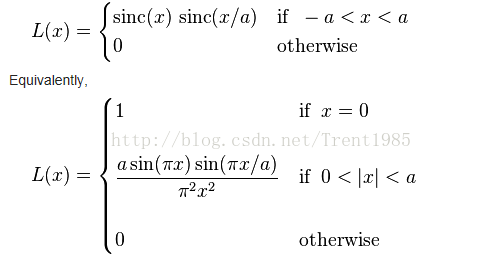
Fig.6 Lanczos
通常,这个a取2或者3,a=2时,该算法适用于图像缩小插值;a=3时,该算法适用于放大插值;对应不同a值得Lanczos插值曲线如上图6所示;上述的公式分别为连续和离散的公式。我们根据输入点X的位置,确定对应window中不同位置的权重L(x),然后对模板中的点值取加权平均,公式如下:
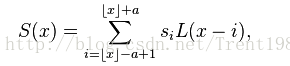
这个S(x)即为X处的插值结果。
根据上述一维插值,推广得到多维插值公式如下(这里以二维为例):

上述内容是对不同插值算法简单的进行了介绍,如果不明白可以查找相关知识。
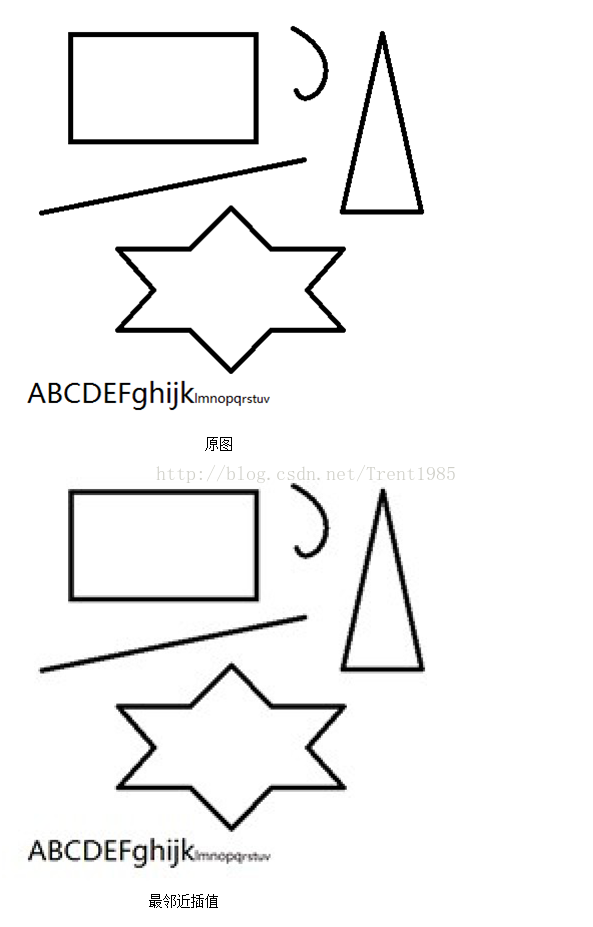
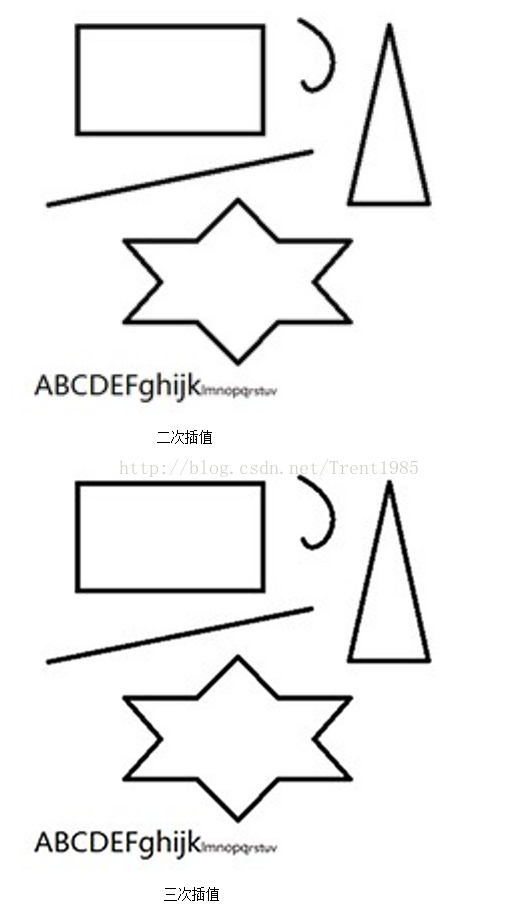
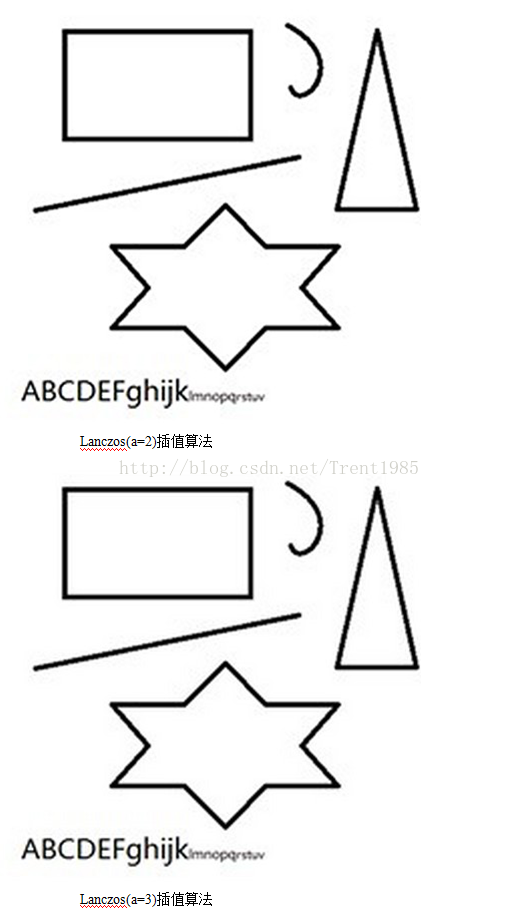
现在我们来看下相应的效果图:
上面的一组效果图均是先将原图缩小50%,然后使用不同算法放大到原图大小得到的。由上面这组图我们可以发现,效果最差的是最邻近插值算法,效果最好的是双线性三次插值,Lanczos算法跟三次插值大致一致;
由于编程语言不同,可能会造成耗时的差距,但是,对于同一种语言,统计得出:最邻近插值速度最快,三次插值速度最慢,而Lanczos算法与二次插值相仿。
综上,Lanczos插值具有速度快,效果好,性价比最高的优点,这也是目前此算法比较流行的原因。
a00 + a10x + a01y + a20x2 + a11xy + a02y2 + a21x2y + a12xy2 + a22x2y2 + a30x3 + a03y3 + a31x3y + a13xy3 + a32x3y2 + a23x2y3 + a33x3y3
或者更简单的形式 :
双三次插值方法能够克服双线性插值和最邻近插值算法的缺点。计算精度比较高,插值效果较最近邻插值法和双线性插值法好,但是计算量大。在图像领域中,该方法考虑一个浮点坐标(i+u,j+v)周围的16个邻点,目标像素值f(i+u,j+v)可由如下插值公式得到:
f(i+u,j+v)=[A]×[B]×[C]
[A]=[S(u+1) S(u+0) S(u-1) S(u-2)]