DLT-04-非线性回归

本文是**深度学习入门（deep learning tutorial, DLT）**系列的第三篇文章，主要介绍一下非线性回归。想要学习深度学习或者想要了解机器学习的同学可以关注公众号GeodataAnalysis，我会逐步更新这一系列的文章。

正如线性回归的含义就是研究变量之间存在怎样的线性关系，非线性回归同样是研究变量之间存在怎样的关系，只是这种关系不再是线性的了。求解非线性回归的方法有很多，在这里只介绍比较简单常用的一种方法，即将非线性回归问题转化为线性回归问题进行求解。

1 原理介绍

下面我们通过具体实例介绍一下非线性回归的原理，先看一下下图。

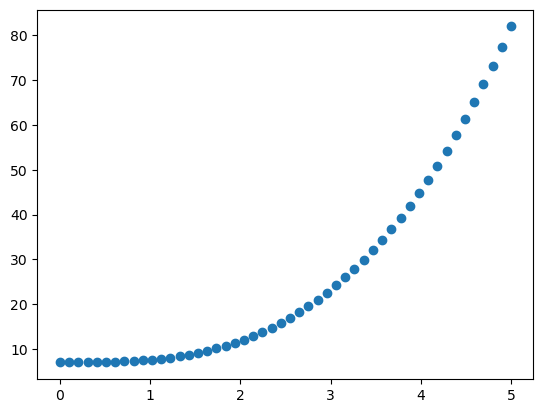
可以很明显的看出，x 和 y 之间不是简单的线性关系，因此无法对这组数据使用线性回归的方法。本文所讲的非线性回归，就是用来处理这种问题的。细心的读者应该发现：上图很像常见的二次函数的图像。这正是非线性回归中很重要的思想，即先发现数据中可能存在的除线性关系外的其他函数关系。此时再画出 $x^2$ 和 y 之间的关系图，如下图所示：

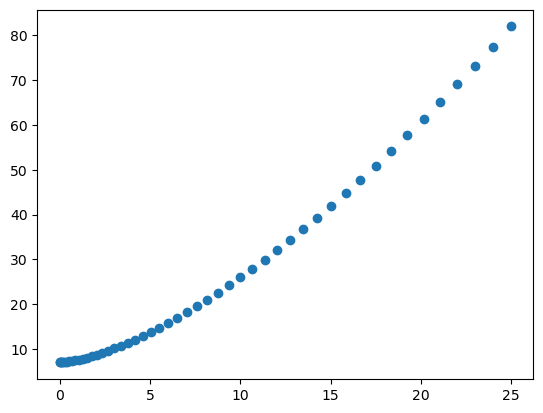
从上图可以看出，$x^2$ 和 y 的关系变得更加线性了，当然中间还是稍有弯曲。基于此，继续尝试 $x^3$ 或 $x^4$，画出 $x^3$ 和 y 之间的关系图，如下图所示：

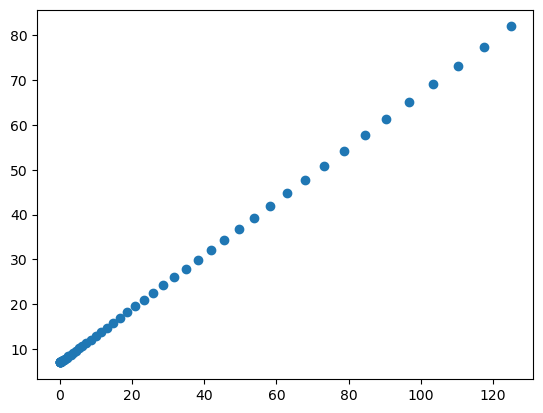
从上图可以看出，$x^3$ 和 y 之间的关系看起来已经非常接近线性了。这样，就可以用线性回归的方法建立它们之间的关系模型。具体步骤如下:

（1）因为 $x^3$ 和 y 之间存在线性关系。因此可以提出一个新的变量 $x^{\prime }$，它的值就等于 $x^3$ 的值。那么，y 和 $x^{\prime }$ 之间的关系就可以表示为：

$$y=\omega x^{\prime }+b$$

（2）利用线性回归的方法，来求解两个未知数 $\omega$ 和 $b$。在这个例子中，求得 $\omega =0.6$，$b=7$。于是得到 y 和 $x^{\prime }$ 之间的关系为：

$$y=0.6x^{\prime }+7$$

（3）最后，把 $x^{\prime }=x^3$ 代回，就得到 y 和 x 之间的关系：

$$y=0.6x^3+7$$

从上面的例子可以看出，只要找到和 y 存在线性关系的那个 $x^3$，非线性回归问题也就被转化为了一元线性回归问题。需要注意的是，并非所有的非线性回归问题都如上面的例子这么简单，即等号右边除常数外只是一个单项式。在某些情况下，因变量 y 还可能同时与 $x^3$、$x^2$ 和 $x$ 存在线性关系，即等号右边除常数外为多项式。读到这里，看过前面文章的读者应该就能想到，这不就变成多元线性回归问题了吗。是的，这种情况只需要采取多元线性回归的思路去求解即可，其关系可以表示为：

$$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3$$

其中，$x_1$、$x_2$ 和 $x_3$ 分别表示 $x^3$、$x^2$ 和 $x$。

2 生成测试数据

我们采用多项式 $y=1.5\ast x^3+0.6\ast x^2+4\ast x+3$ 来生成因变量数据，自变量为-5 到 5 之间的小数。为了模拟真实的数据分布，我们又给因变量添加了随机噪声。具体代码和可视化结果如下：

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-5, 5, 100)

y = 1.5*x**3 + 0.6*x**2 + 4*x + 3
y2 = y + 20 * np.random.randn(y.size)

plt.scatter(x, y2)
plt.plot(x, y, 'k-');

3 数据预处理

通过第一节的原理分析我们已经知道非线性回归可以转化为一元线性回归或多元线性回归，因此其训练模型在假设函数、损失函数、梯度下降等方面的计算公式和一元线性回归或多元线性回归是一样的。是以我们完全可以采用前两篇文章所学的方法求解非线性回归问题，区别仅在于需要对输入变量做一些变换，如将 $x$ 变为 $x^3$。

由于本文的例子中，等号右边除常数外是一个多项式，因此我们采用上一篇文章介绍的多元线性回归的方法求解该模型。这里值得一说的是，多元线性回归事实上也可以转化为一元线性回归，只需要在输入数据时将其他变量的值都设为 0 即可。

在我们这个例子中，需要对输入数据进行如下处理，代码如下：

x2 = np.vstack([
    x**3,
    x**2,
    x
])
x2.shape

((3, 100)

4 训练与预测

这里我们使用上一篇文章多元线性回归中封装的模型MutiLinearRe进行训练和预测，具体代码如下：

model = MutiLinearRe(input_shape=x2.shape)
model.fit(x2, y2, epoch_size=100, batch_size=80,
		  learning_rate=0.0001, normalization=False)
plt.plot(model.loss);

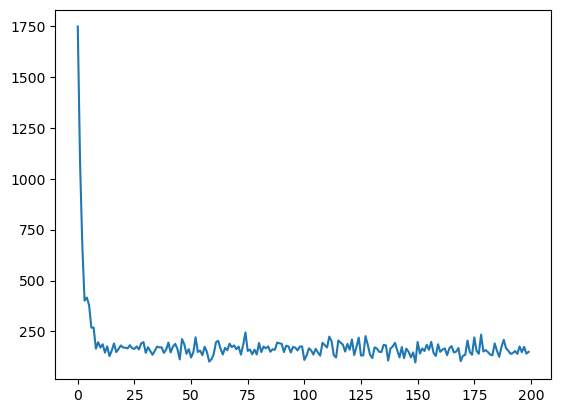
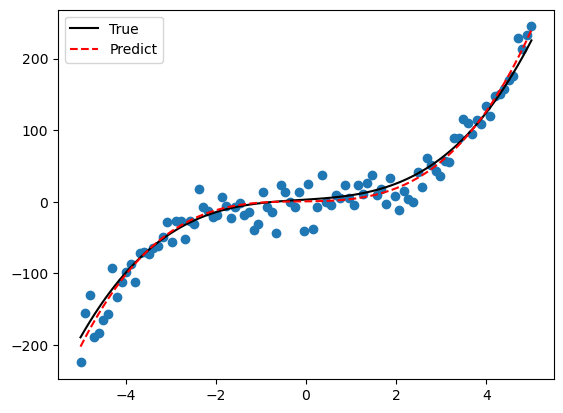
plt.scatter(x, y2)
plt.plot(x, y, 'k-', label='True')
plt.plot(x, model.predict(x2), 'r--', label='Predict')
plt.legend();